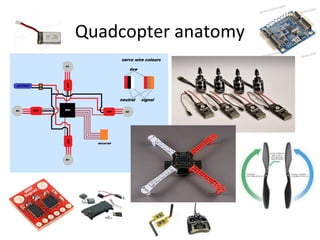
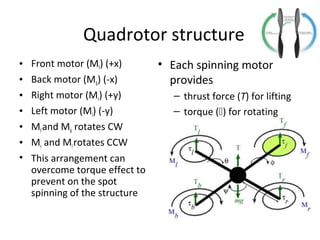
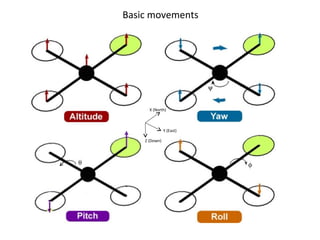
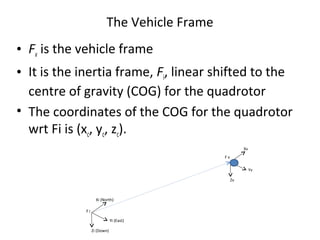
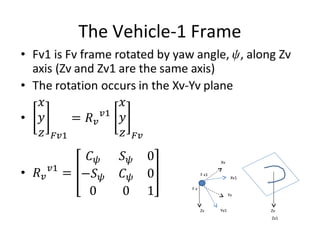
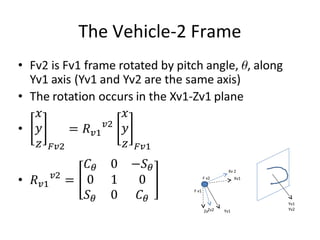
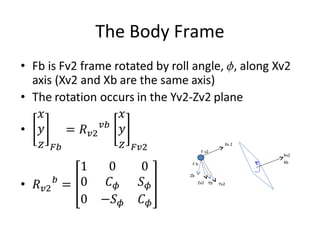
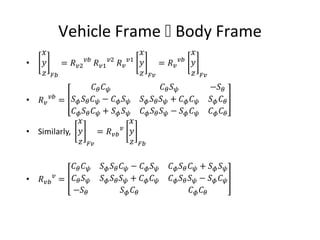
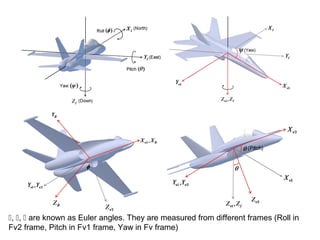
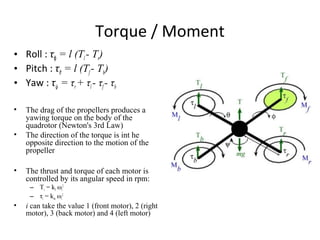
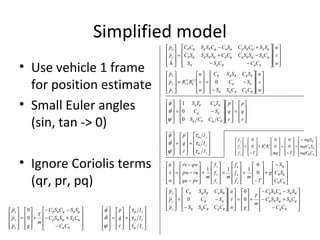
The document describes the anatomy and dynamics of a quadrotor unmanned aerial vehicle (UAV). It discusses the first manned quadrotor flight in 1907 and advantages of quadrotors such as vertical take-off and landing. Key components of quadrotor structure and motion including motors, frames of reference, state variables, and kinematic and dynamic equations are presented. Thrust forces from each motor and gravity are expressed as components of the total force acting on the quadrotor.