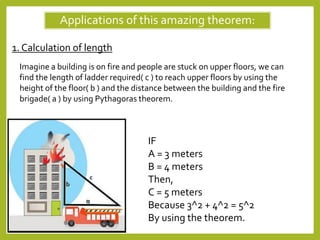
The document discusses the Pythagorean theorem and its applications. It begins by introducing Pythagoras and the theorem, which states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. It then provides examples of how the theorem can be used in construction, navigation, determining the size of a TV screen, and ensuring square corners in buildings.

1. MATHEMATICS
SUMMER HOLIDAY
HOMEWORK
ON

2. INTRODUCTION
We all know that Pythagoras of Samoswas
was credited with many mathematical and
scientific discoveries, including the
Pythagorean theorem as the name suggests.
He was an ancient Greek philosopher
whose political and religious teachings
influenced the philosophies of great
philosophers like Plato and Aristotle.
One of the most important contributions of
Pythagoras is the “Pythagoras theorem”,
which has proven to be a very useful
technique for construction and navigation in
almost every field of work.

3. PythagorasTheorem
…When a triangle has a right angle (90°) ...
... and squares are made on each of the three sides, ...
... then the biggest square has the exact same area as the other two
squares put together!

4. "Pythagoras'Theorem" can also be written in one short
equation:
The Pythagoras theorem states that the square of the length
of the hypotenuse is equal to the sum of squares of the
lengths of other two sides of the right-angled triangle.
By definition,
It is one of the most fundamental theorems in mathematics
and it defines the relationship between the three sides of a
right-angled triangle.

5. Applications of this amazing theorem:
Imagine a building is on fire and people are stuck on upper floors, we can
find the length of ladder required( c ) to reach upper floors by using the
height of the floor( b ) and the distance between the building and the fire
brigade( a ) by using Pythagoras theorem.
1. Calculation of length
IF
A = 3 meters
B = 4 meters
Then,
C = 5 meters
Because 3^2 + 4^2 = 5^2
By using the theorem.

6. 2. Architecture and Construction
The PythagoreanTheorem allows us to calculate the
length of the diagonal connecting two straight lines.
This application is frequently used in architecture,
woodworking, or other physical
construction projects.
For instance, if we are building a
sloped roof and we know the height
of the roof and the length for it to
cover, we can use the Pythagorean
Theorem to find the diagonal length
of the roof's slope and use this
information to cut properly sized beams to support the
roof.

7. 3. Navigation
•The PythagoreanTheorem is very useful for navigation.
•We can use it and two lengths to find the shortest distance.
•For example, if we are at sea and navigating to a point that is 300
km north and 400 km west, we can use the theorem to find the
distance from our ship to that point and calculate the direction
we would need to follow to reach that point.
•The distances north and west will be the two legs of the triangle,
and the shortest line connecting them will be the hypotenuse.
•The same principles can be used for air navigation. For instance,
a plane can use its height above the ground and its distance from
the destination airport to find the correct place to begin a descent
to that airport.

8. 4. What sizeTV to buy?
Mr. James saw an advertisement of aT.V.in the newspaper
where it is mentioned that theT.V. is 16 inches high and 14 inches
wide.
To calculate the diagonal length of its screen, Mr. James used
Pythagoras’ theorem as:
16^2 + 14^2 = 256 + 196 = C^2 √452 = 21 inches approx.
21

9. 5. Square angles in buildings
To make sure that the buildings are in
square shape, PythagoreanTheorem is
used.
A set of Pythagorean triplets are used
to construct square corners between
two walls.
For example a 5 meter by 12 meter by
13 meter triangle will always be a right
angled triangle.
The workers will set out a triangle with these lengths to construct a
square corner between the two walls, and the builder will know whether
they are working on a right track if the proper lengths of the strings are
used during construction of the right angled triangle.