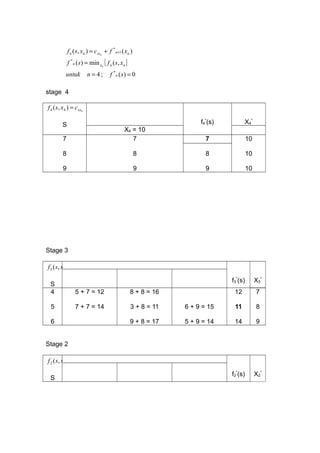
Dokumen ini membahas prosedur dinamis untuk mengoptimalkan rute pengiriman barang dari kota asal ke tujuan dengan biaya terendah melalui kota persinggahan. Beragam rute yang mungkin dilalui dengan biaya masing-masing dihitung dan metode rekursif maju dan mundur diterapkan untuk menentukan rute terbaik. Rute optimal ditemukan dengan nilai minimum sebesar 21.

1. PROGRAM DINAMIS
pengiriman barang berangkat dari kota asal (1) ke tujuan akhir pengiriman (10)
yang dapat melalui beberapa kota lain sebagai tempat persinggahan
sementara. Gambar berikut menunjukkan route yang mungkin dilalui dengan
biaya-biayanya. Tujuannya adalah memilih route yang mempunyai biaya
minimum.
5
Persoalan ini dapat diselesaikan dengan menjumlahkan semua biaya dari
semua route yang mungkin dilalui. Bila hal ini dilakukan, maka penyelesaiannya
adalah :

2. No. Nama Route Jumlah Biaya
1 1 – 2 – 4 – 7 - 10 8 + 4 + 5 + 10 = 27
2 1 – 2 – 4 – 8 – 10 8 + 4 + 5 + 8 = 28
3 1 – 2 – 5 – 7 – 10 8 + 6 + 7 + 10 = 31
4 1 – 2 – 5 – 8 – 10 8 + 6 + 3 + 8 = 25
5 1 – 2 – 5 – 9 - 10 8 + 6 + 6 + 9 = 29
6 1 – 3 – 4 – 7 - 10 5 + 9 + 5 + 10 = 29
7 1 – 3 – 4 – 8 - 10 5 + 9 + 8 + 8 = 30
8 1 – 3 – 5 – 7 - 10 5 + 5 + 3 + 10 = 23
9 1 – 3 – 5 – 8 - 10 5 + 5 + 3 + 8 = 21 * min
10 1 – 3 – 5 – 9 - 10 5 + 5 + 6 + 9 = 25
11 1 – 3 – 6 – 8 - 10 5 + 4 + 9 + 8 = 26
12 1 – 3 – 6 – 9 - 10 5 + 4 + 5 + 9 = 23
Prosedur Penyelesaian
Langkah maju Forward, perhitungan bergerak dari (1) hingga (10) dan
langkah mundur Backward perhitungan bergerak dari (10) hingga (1)
Notasi yang digunakan
nX
: Variabel keputusan sebagai tempat persinggahan pada stage n
(n=1,2,3,4), Maka route yang dilalui adalah 43211 xxxx →→→→
;
4x = kota (state) 10
),( nn xsf
: Ongkos total jika berada di kota S dan memilih xn sebagai tempat
persinggahan berikutnya. Untuk s dan n tertentu, x*
n adalah xn yang
meminimumkan
),( nn xsf
: )(*
sf n
:Nilai mimimum dari
),( nn xsf
sehingga :
)(*
sf n
:
),( *
nn xsf

3. nsxc
: ongkos dari kota s ke kota xn
contoh langkah maju :
Persamaan rekursifnya :
1. Persamaan Rekursif Maju
)(),( 1
*
nnsxnn xfcxsf n
−+=
untuk n = 1 : 0)(0
*
=sf dan
1
),( 11
*
sxcxsf =
{ }nnxn xsfsf n
,(min)(*
=
Stage 1
1sxc
S F1
*
(s) X1
*
X1 = 1
2
3
8
5
8
5
1
1
Stage 2
)(),( 2122 2
xfcxsf sx +=
S f2
*
(s) X2
*
4
5
6
4 + 8 = 12
6 + 8 = 14
9 + 5 = 14
5 + 5 = 10
4 + 5 = 9
12
10
9
2
3
3
Stage 3

4. )(),( 3233 3
xfcxsf sx +=
S
f3
*
(s) X3
*
7
8
9
5 + 12 = 17
8 + 12 = 20
7 + 10 = 17
3 + 10 = 13
6 + 10 = 16
9 + 9 = 18
5 + 9 = 14
17
13
14
4,5
5
6
Stage 4
)(),( 4344 4
xfcxsf sx +=
S f4
*
(s) X4
*
10 10 + 17 = 27 8 + 13 = 21 9 + 14 = 23 21 8
Untuk langkah maju, penyelesaian akhir untuk menentukan route optimal
dimulai dari stage 4.
Pada stage 4 ; x*
4 = 8
Pada stage 3 ; untuk s = 8 ; x*
3 = 5
Pada stage 2 ; untuk s = 6 ; x*
2 = 3
Pada stage 1 ; untuk s = 3 ; x*
1 = 1
Maka :
(x*
1 , x*
2 , x*
3 , x*
4 ) = ( 1, 3, 5, 8, 10 )
dengan nilai minimum = 21
2. Persamaan rekursif Mundur

5. { }
0)(;4
,(min)(
)(),(
*
*
1
*
==
=
+= +
sfnuntuk
xsfsf
xfcxsf
n
nnxn
nnsxnn
n
n
stage 4
4
),( 44 sxcxsf =
S f4
*
(s) X4
*
X4 = 10
7
8
9
7
8
9
7
8
9
10
10
10
Stage 3
)(),( 3
*
433 3
xfcxsf sx +=
S
f3
*
(s) X3
*
4
5
6
5 + 7 = 12
7 + 7 = 14
8 + 8 = 16
3 + 8 = 11
9 + 8 = 17
6 + 9 = 15
5 + 9 = 14
12
11
14
7
8
9
Stage 2
)(),( 2
*
322 2
xfcxsf sx +=
S
f2
*
(s) X2
*

6. 2
3
4 + 12 = 16
9 + 12 = 21
6 + 11 = 17
5 + 11 = 16 4 + 14 = 18
16
16
5
5
Stage 1
)( 1
*
21
xfcsx +
S
f1
*
(s) X1
*
1 8 + 16 = 24 5 + 16 = 21 21 3
Stage 1 ; s = 1 maka x*
1 = 3 Stage 3 ; s = 5 maka x*
3 = 8 Stage
2 ; s = 3 maka x*
2 = 5 Stage 4 ; s = 8 maka x*
4 = 10
( x*
1 , x*
2 , x*
3 , x*
4 ) = ( 1, 3, 5, 8, 10 ) dengan nilai minimum 21

7. 2
3
4 + 12 = 16
9 + 12 = 21
6 + 11 = 17
5 + 11 = 16 4 + 14 = 18
16
16
5
5
Stage 1
)( 1
*
21
xfcsx +
S
f1
*
(s) X1
*
1 8 + 16 = 24 5 + 16 = 21 21 3
Stage 1 ; s = 1 maka x*
1 = 3 Stage 3 ; s = 5 maka x*
3 = 8 Stage
2 ; s = 3 maka x*
2 = 5 Stage 4 ; s = 8 maka x*
4 = 10
( x*
1 , x*
2 , x*
3 , x*
4 ) = ( 1, 3, 5, 8, 10 ) dengan nilai minimum 21