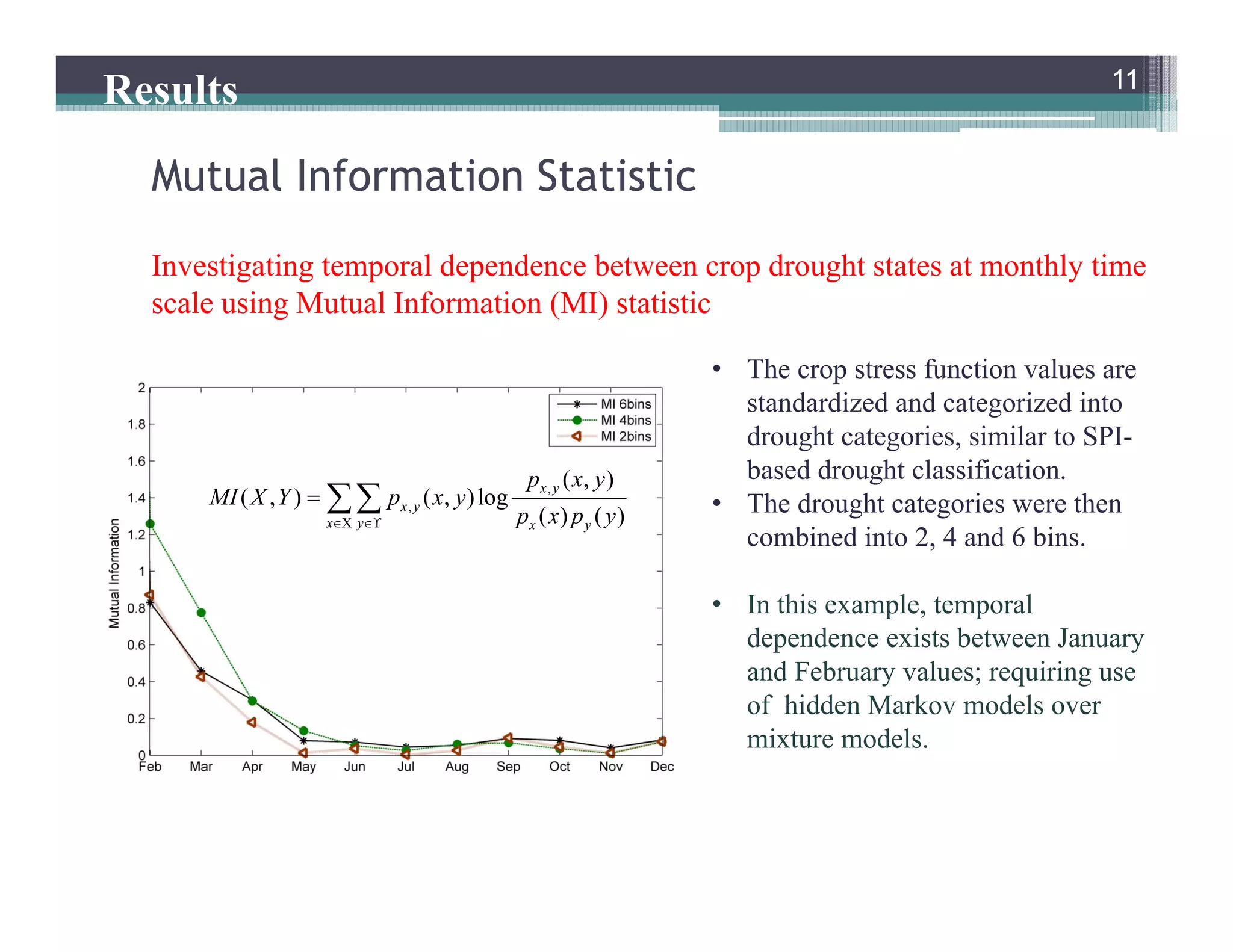
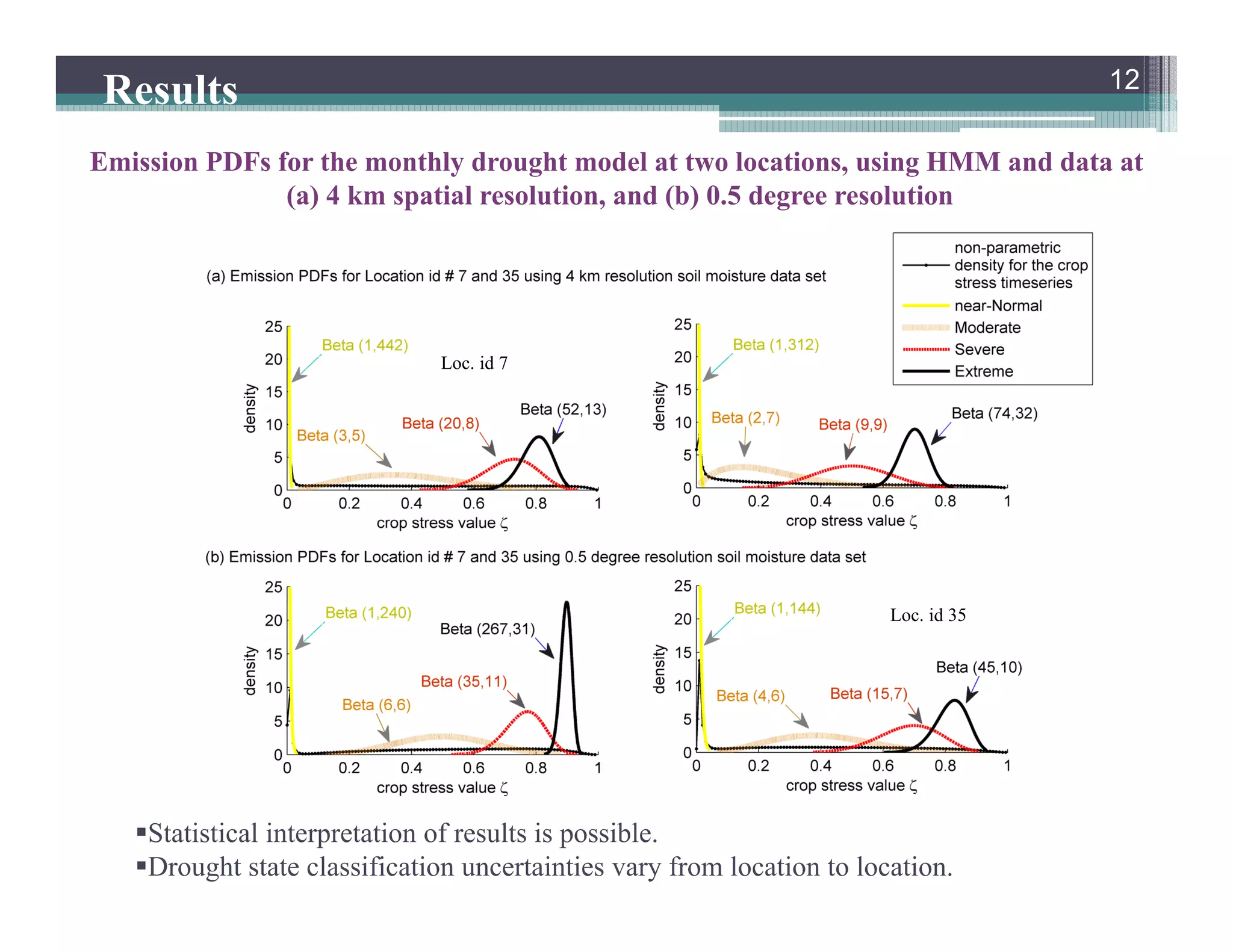
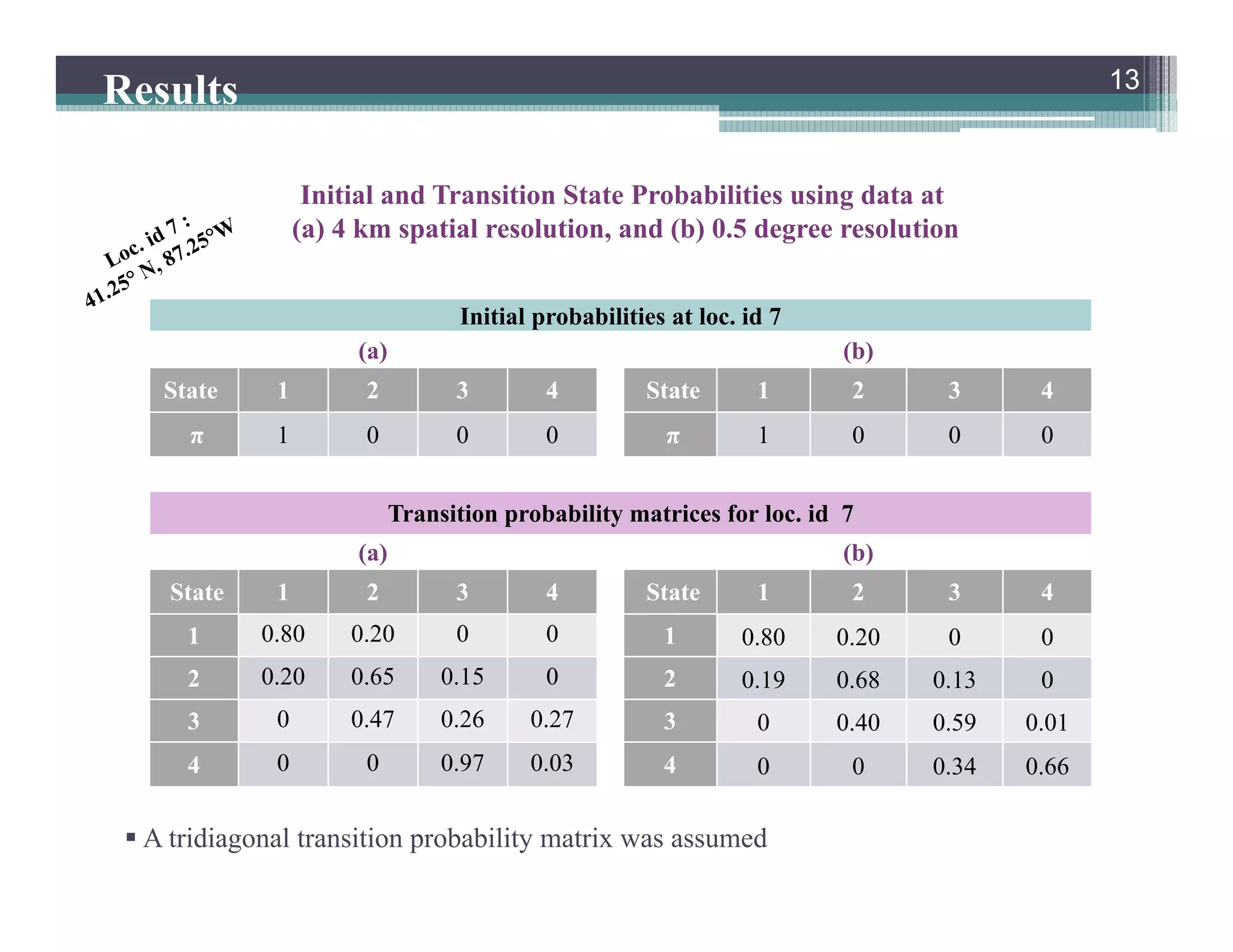
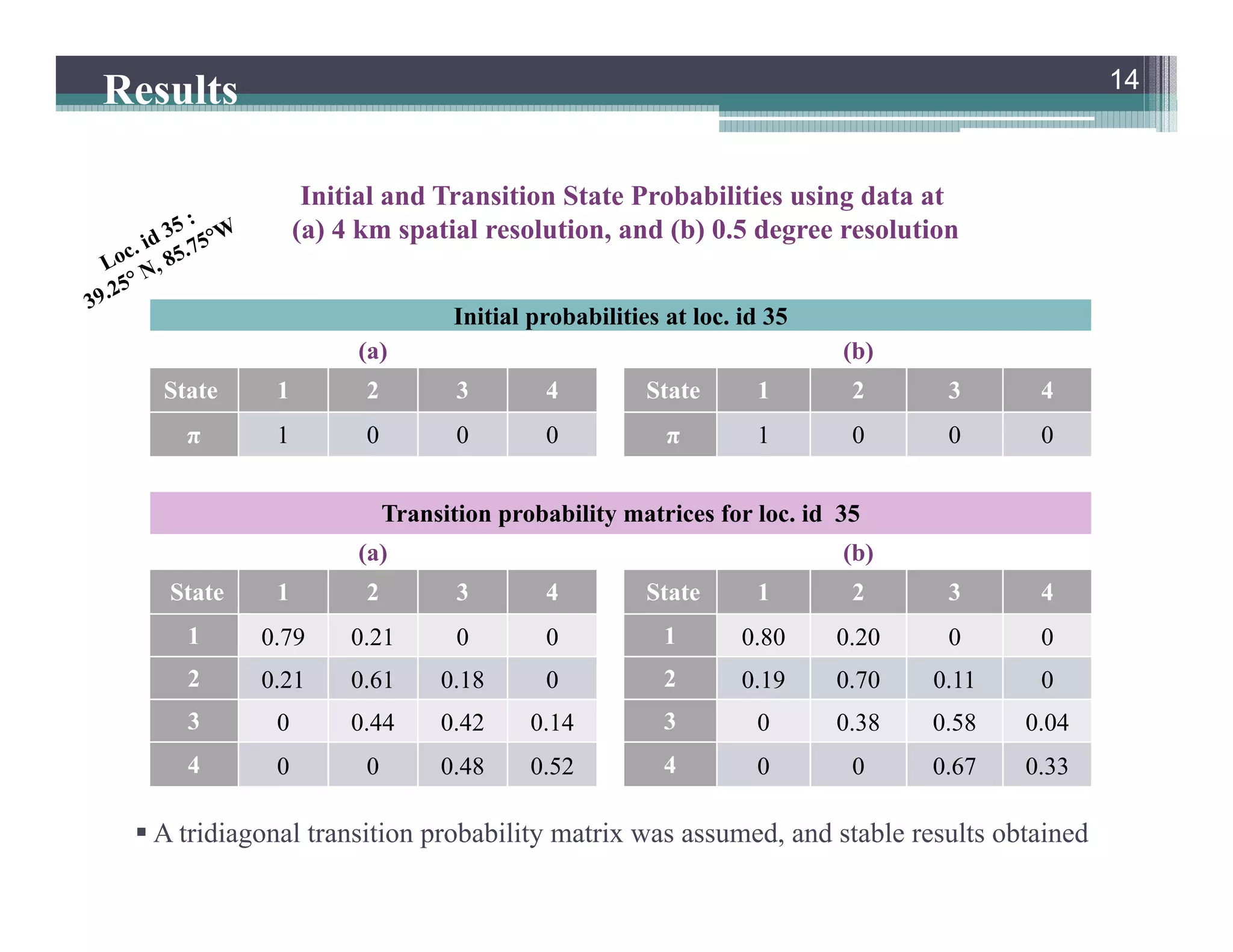
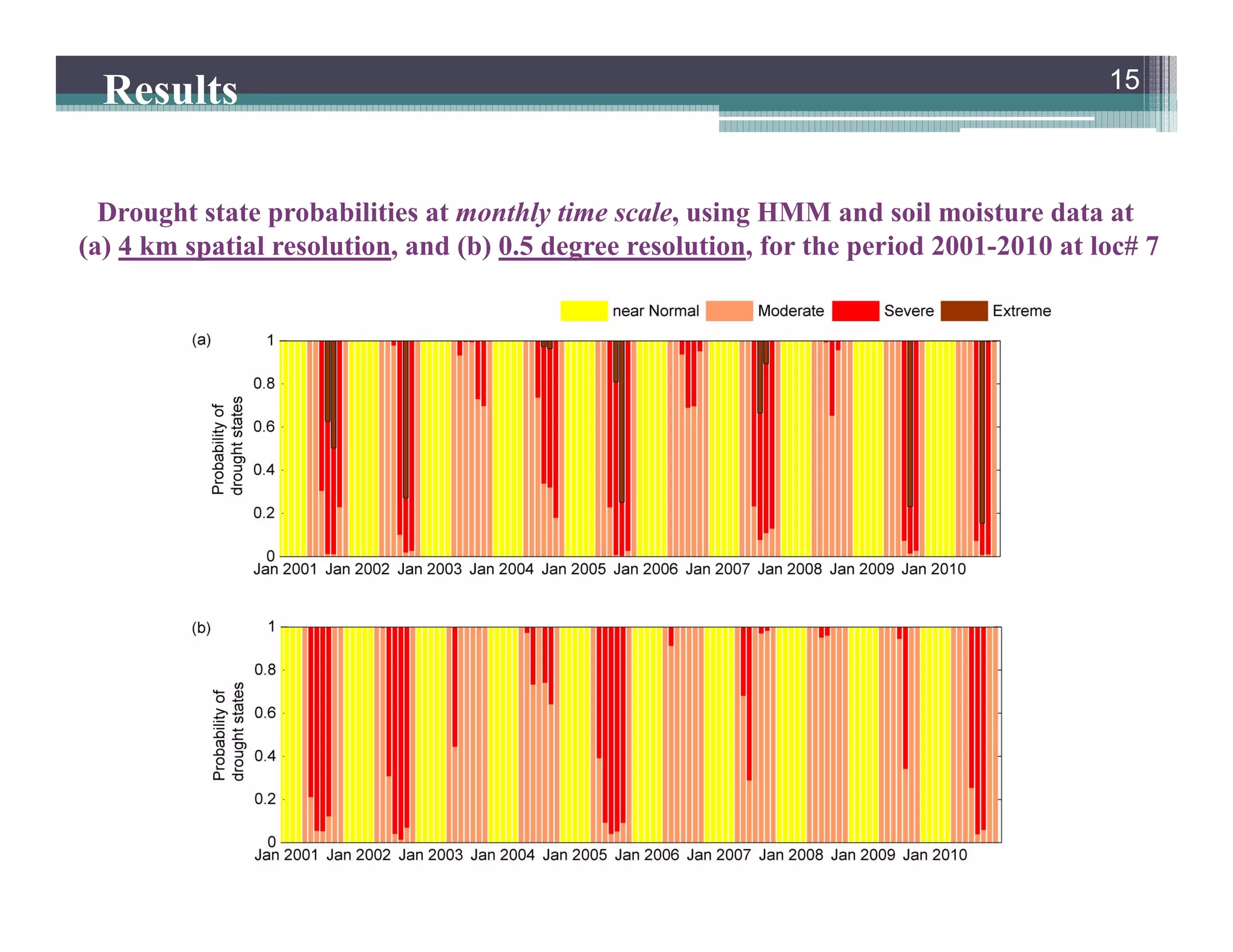
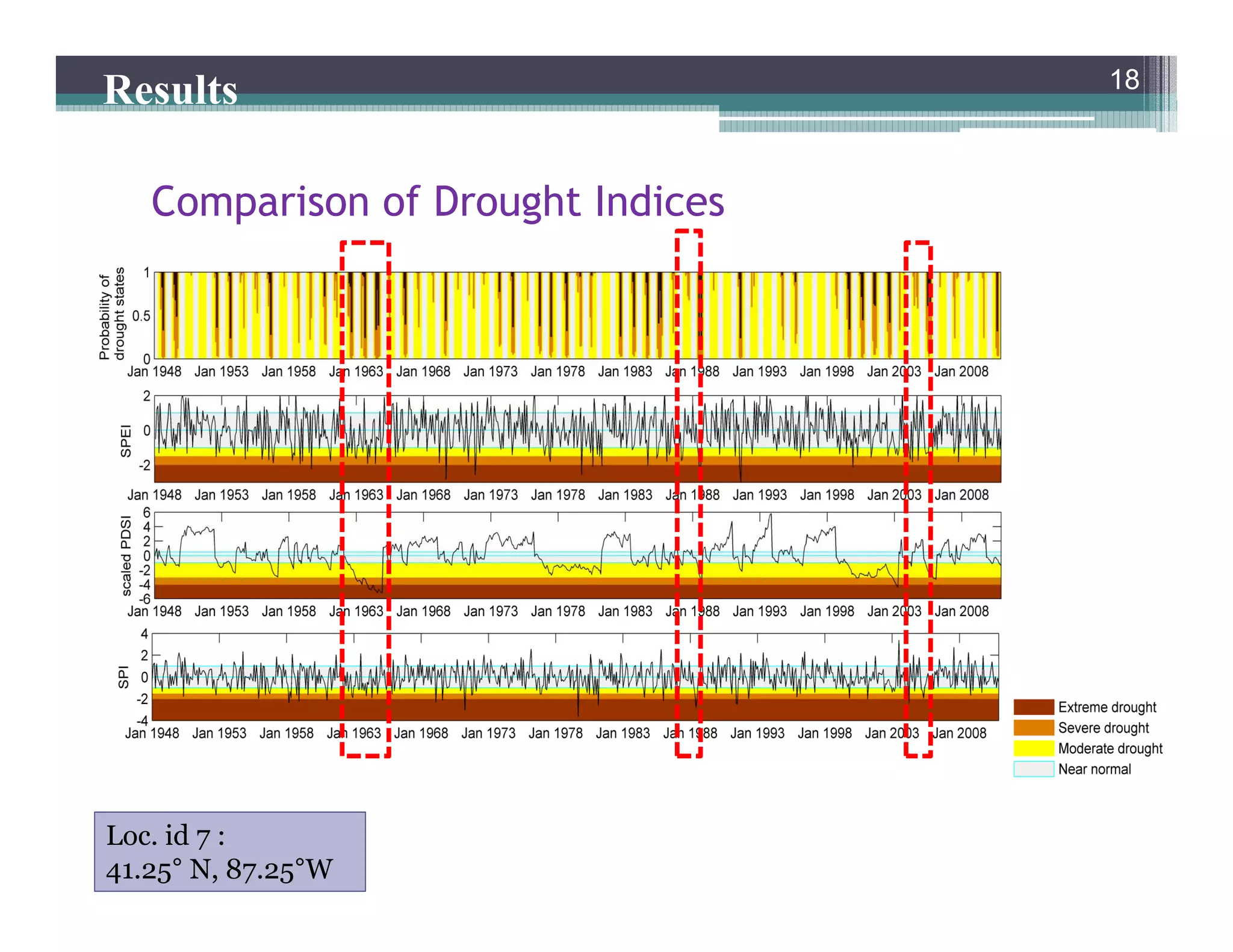
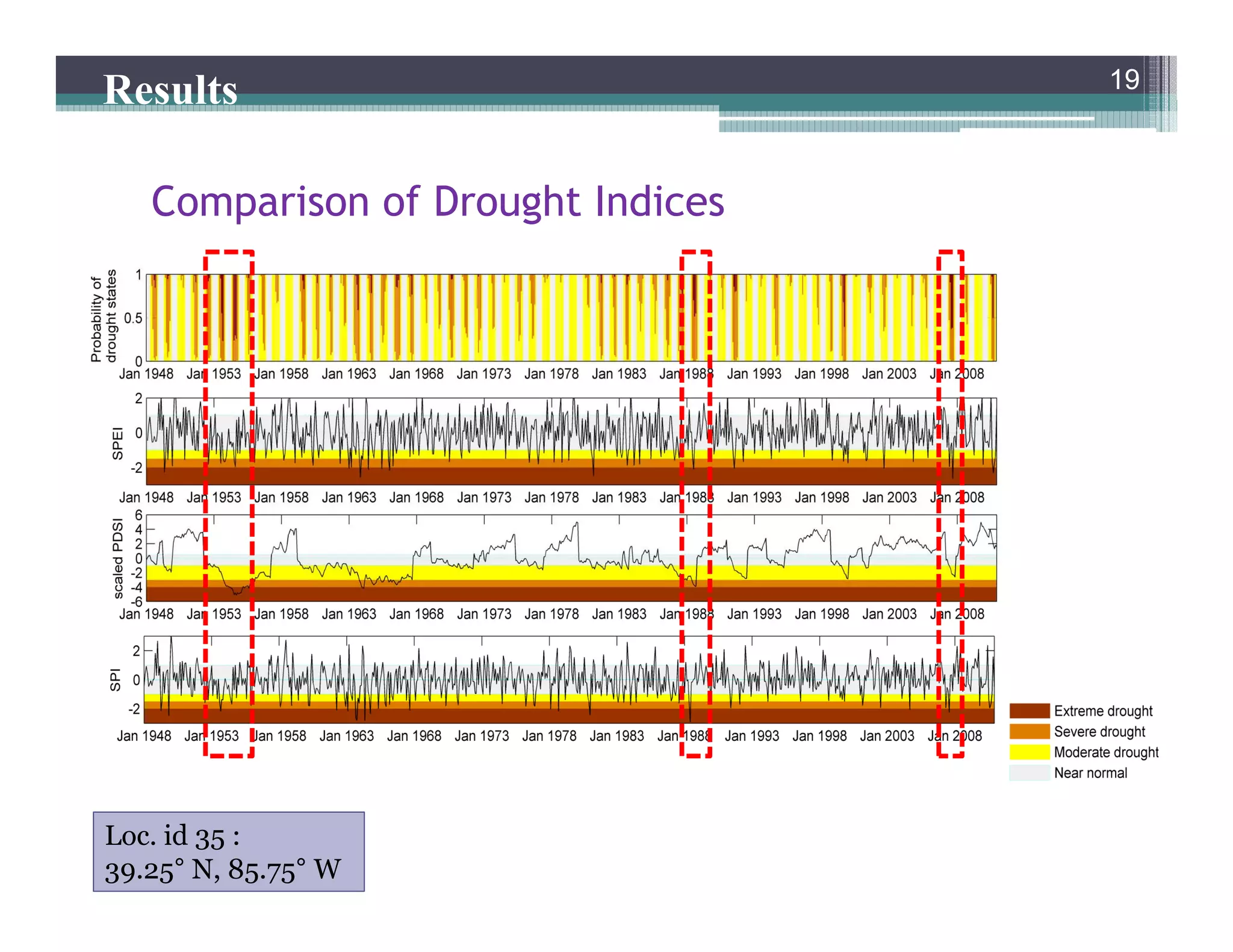
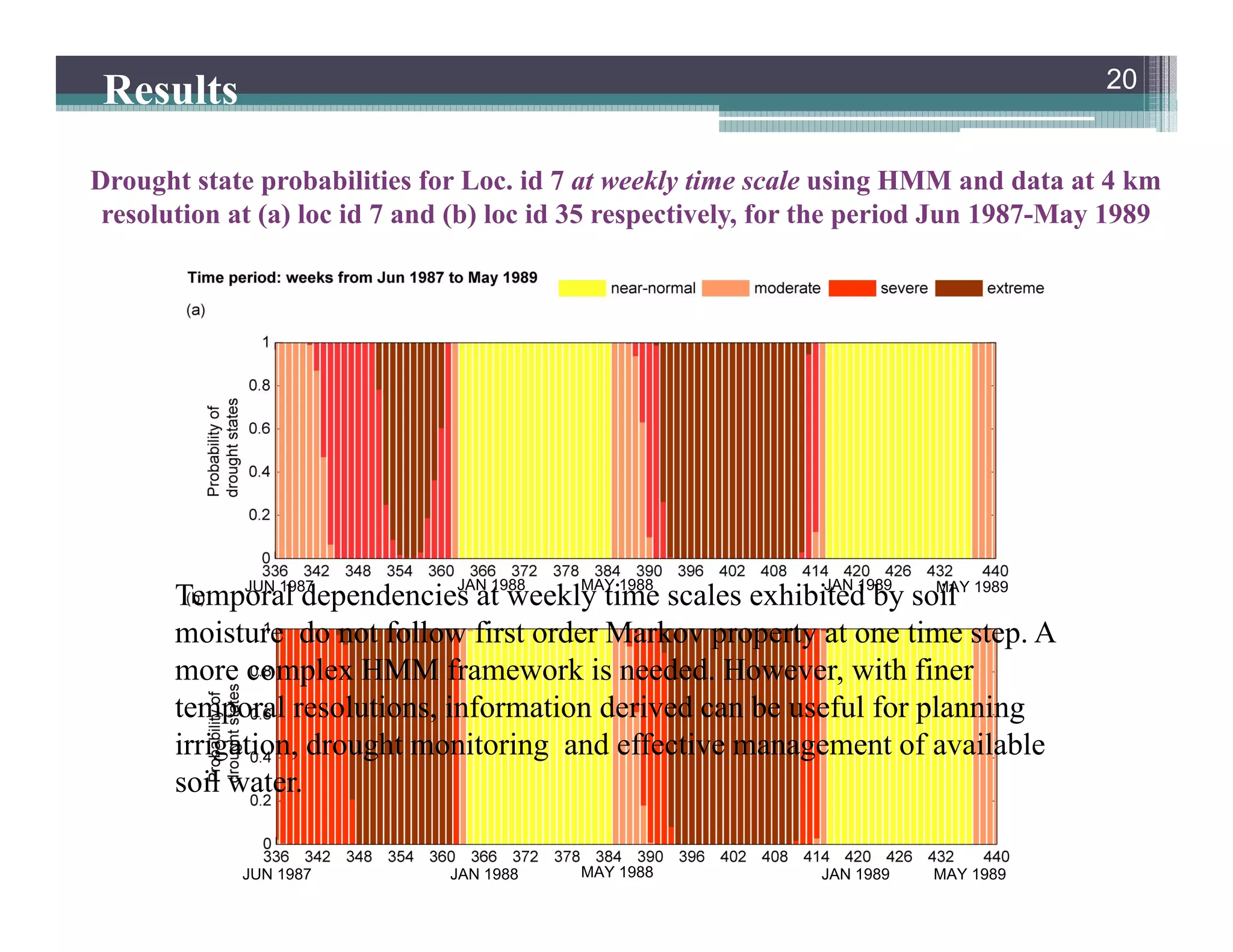
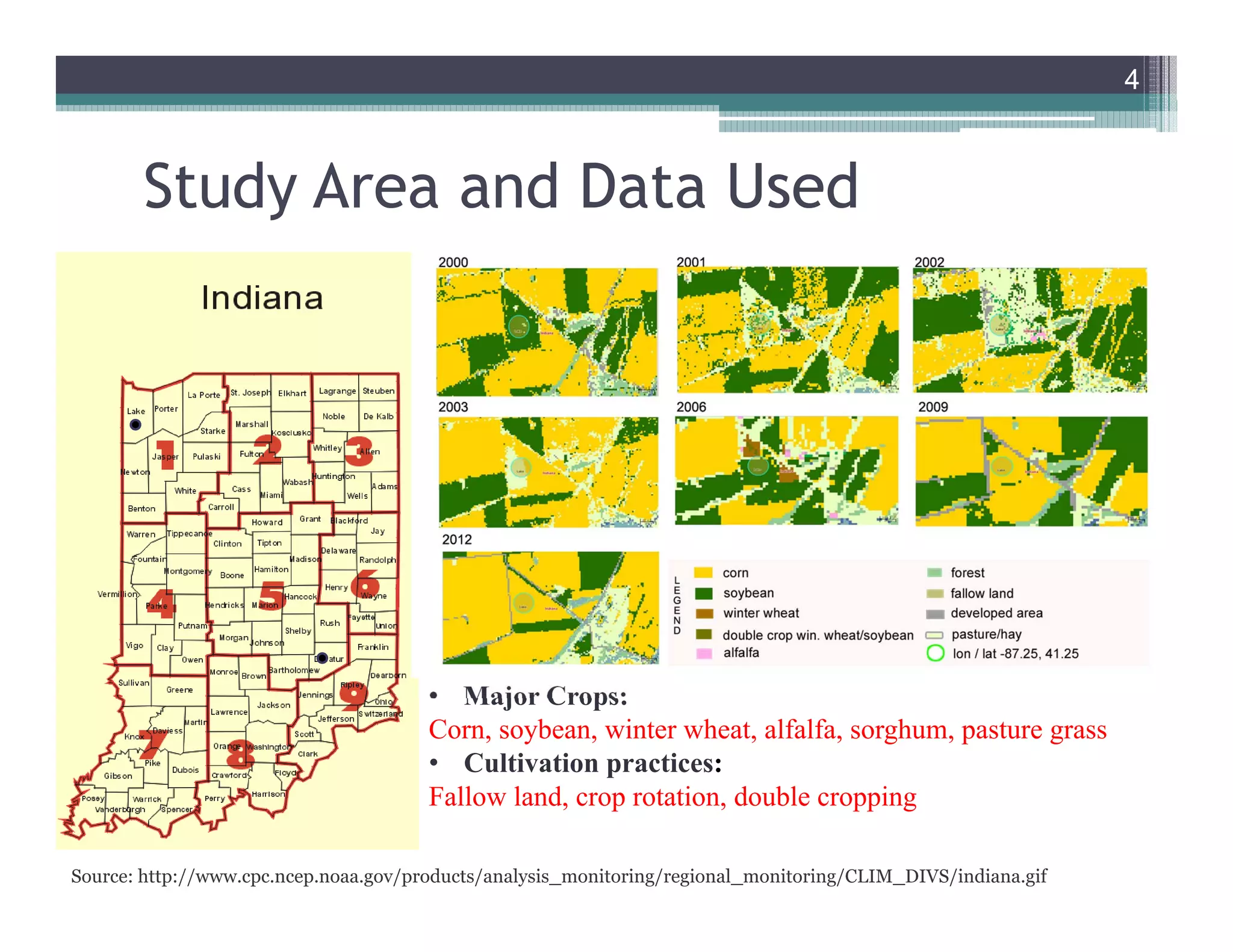
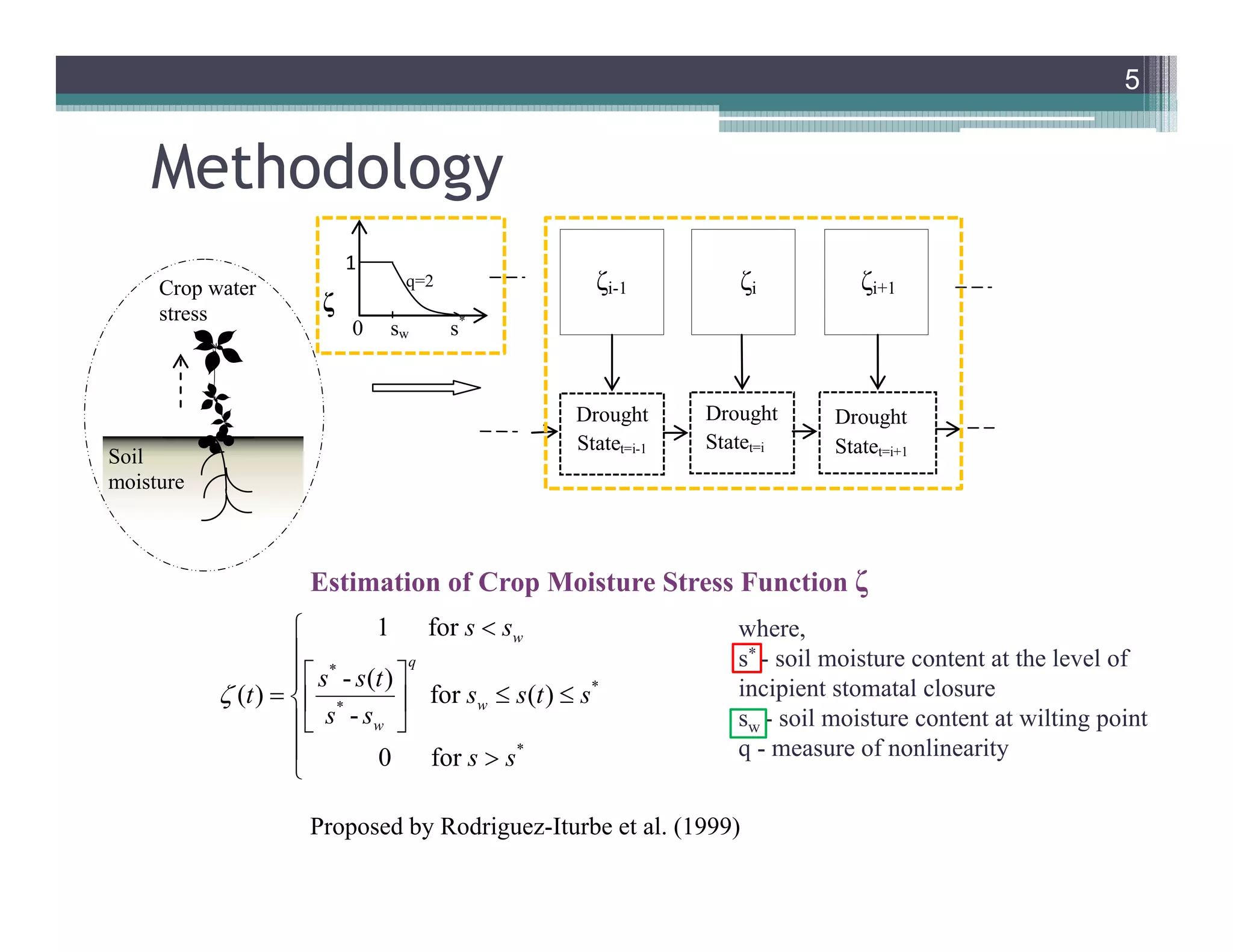
This document summarizes a study that developed a probabilistic model for assessing agricultural droughts using graphical models. The study used hidden Markov models (HMMs) to relate unobserved drought states to observed crop water stress levels. HMMs were estimated using soil moisture and crop data at different spatial scales in Indiana. Results showed drought classifications varied by location and resolution. The probabilistic approach provided uncertainty estimates not available from other drought indices and identified additional drought events. Weekly analyses revealed complex temporal dependencies requiring advanced HMM frameworks.

1. Probabilistic Assessment of
Agricultural Droughts using
Graphical Models
69th SWCS International Annual Conference
Lombard, IL | July 29, 2014
Presented by
Meenu Ramadas
PhD Student
Lyles School of Civil Engineering
Purdue University
Co-authors
Dr. Rao S Govindaraju
Dr. Indrajeet Chaubey
Dr. Dev Niyogi
Dr. C X Song

2. Introduction
• Agricultural drought conditions are, by and large, determined by soil
moisture rather than by precipitation.
• Since water needs vary with crops, agricultural droughts in a region can
be assessed better, if crop responses to soil water deficits are also
accounted for in the drought index.
• A probabilistic assessment would convey the uncertainty in agricultural
drought classification that popular indices (Standardized Precipitation
Index, SPI; Palmer Drought Severity Index, PDSI; Standardized
Precipitation Evapotranspiration Index, SPEI) do not provide.
2
2

3. Objectives of the Study
To investigate agricultural drought events in Indiana in a probabilistic
framework using graphical models (hidden Markov models), and compare
the modeling results at different spatial and temporal resolutions.
3
3

4. Study Area and Data Used
4
Data Used:
• Cropland Data Layer (CDL) for 2000-2010 hosted on
CropScape (Han et al., 2012) developed by the National
Agricultural Statistics Service (NASS) of the United States
Department of Agriculture (USDA).
• Soil moisture data, the Climate Prediction Center’s (CPC)
0.5° resolution global monthly datasets (Fan and van den
Dool, 2004)- data from 1948-2010.
• Soil moisture data, daily values at 4 km spatial resolution
from NASA-LIS model from 1981-2010.
• Major Crops:
Corn, soybean, winter wheat, alfalfa, sorghum, pasture grass
• Cultivation practices:
Fallow land, crop rotation, double cropping
Source: http://www.cpc.ncep.noaa.gov/products/analysis_monitoring/regional_monitoring/CLIM_DIVS/indiana.gif
4

5. Methodology
Estimation of Crop Moisture Stress Function ζ
Proposed by Rodriguez-Iturbe et al. (1999)
5
*
*
*
*
1 for
- ( )
( ) for ( )
-
0 for
w
q
w
w
s s
s s t
t s s t s
s s
s s



 
   
 
 
Soil
moisture
q=2
ζ
1
0 sw s*
Crop water
stress
Drought
Statet=i-1
Drought
Statet=i
Drought
Statet=i+1
ζi-1 ζi ζi+1
where,
s* - soil moisture content at the level of
incipient stomatal closure
sw - soil moisture content at wilting point
q - measure of nonlinearity
5

6. Methodology
Graphical model
• A family of distributions that can be efficiently represented by directed or
undirected graph
Hidden Markov Models (HMMs)
• The graph structure in HMMs comprises of hidden nodes in addition to
the observed nodes, such that dependencies exist between these hidden
nodes.
• Outputs of the system are assumed to be dependent on a sequence of
hidden states.
• In this study, the hidden nodes are the latent drought states, while the
observations could be the drought indicator variable (crop water stress).
6
6

7. 7
Source: Fig.1, Sudderth et al. 2010. “Nonparametric Belief Propagation”
Methodology

8. Methodology
Basic Elements of HMM
 Transition probabilities
 Emission densities-a suitable probability distribution with
parameters
 Initial state probabilities
 Constraints:
8
1 2 1 1( | , , , ) ( | )t t t t tP q q q q P q q   
( | )t tP q 
{ , }B  
1{ },s.t. ( ), 1,2, ,i i P q i i K      
1
1
1
1, 1 i
K
i
i
K
ij
j
a K




  


{ }ijA a

9. Methodology
• Parameter estimation consists of determining of the HMM from
the crop water stress time series.
• Continuous Gaussian HMMs are easily modeled. Closed-form expressions
derived for Expectation Maximization (EM) algorithm [Rabiner, 1989].
• Crop stress values are however bounded in the range of [0,1]. Beta
emission distribution was found suitable for the emission model.
Derivation of new parameter estimation formula was performed from first
principles of EM algorithm.
• These expressions are obtained by treating parameter estimation as a
constrained optimization of Probability of Observations given the Model
parameters or P(O|model), subject to constraints, and estimation formula
are developed using Lagrange multipliers technique.
9
{ , , }A B
9

10. Results
10
10

11. Mutual Information Statistic
11
Investigating temporal dependence between crop drought states at monthly time
scale using Mutual Information (MI) statistic
• The crop stress function values are
standardized and categorized into
drought categories, similar to SPI-
based drought classification.
• The drought categories were then
combined into 2, 4 and 6 bins.
• In this example, temporal
dependence exists between January
and February values; requiring use
of hidden Markov models over
mixture models.
,
,
( , )
( , ) ( , )log
( ) ( )
x y
x y
x y x y
p x y
MI X Y p x y
p x p y 
 
11
Results

12. 12
Results
Statistical interpretation of results is possible.
Drought state classification uncertainties vary from location to location.
Loc. id 7
Loc. id 35
Emission PDFs for the monthly drought model at two locations, using HMM and data at
(a) 4 km spatial resolution, and (b) 0.5 degree resolution

13. Initial probabilities at loc. id 7
(a) (b)
State 1 2 3 4 State 1 2 3 4
π 1 0 0 0 π 1 0 0 0
Transition probability matrices for loc. id 7
(a) (b)
State 1 2 3 4 State 1 2 3 4
1 0.80 0.20 0 0 1 0.80 0.20 0 0
2 0.20 0.65 0.15 0 2 0.19 0.68 0.13 0
3 0 0.47 0.26 0.27 3 0 0.40 0.59 0.01
4 0 0 0.97 0.03 4 0 0 0.34 0.66
Initial and Transition State Probabilities using data at
(a) 4 km spatial resolution, and (b) 0.5 degree resolution
13
Results
 A tridiagonal transition probability matrix was assumed

14. 14
Results
 A tridiagonal transition probability matrix was assumed, and stable results obtained
Initial probabilities at loc. id 35
(a) (b)
State 1 2 3 4 State 1 2 3 4
π 1 0 0 0 π 1 0 0 0
Transition probability matrices for loc. id 35
(a) (b)
State 1 2 3 4 State 1 2 3 4
1 0.79 0.21 0 0 1 0.80 0.20 0 0
2 0.21 0.61 0.18 0 2 0.19 0.70 0.11 0
3 0 0.44 0.42 0.14 3 0 0.38 0.58 0.04
4 0 0 0.48 0.52 4 0 0 0.67 0.33
Initial and Transition State Probabilities using data at
(a) 4 km spatial resolution, and (b) 0.5 degree resolution

15. Drought state probabilities at monthly time scale, using HMM and soil moisture data at
(a) 4 km spatial resolution, and (b) 0.5 degree resolution, for the period 2001-2010 at loc# 7
15
Results

16. • At the two locations, HMM results were found to be different,
transition probabilities as well as the emission pdfs varied from place to
place.
• The emission pdfs for drought states evolved differently while using
data of different resolutions at the same grid point. The drought
classification ,as a result, changes with the data used, especially
between the severe and extreme categories.
• Hence, a large number of extreme drought events are captured by the
high resolution model, and not by the CPC data-based model.
16
HMMs at different locations and spatial resolutions
16
Results

17. • Comparison of drought events identified by the proposed index and
indices such as SPEI, PDSI and SPI was performed.
• Given that proper definitions of corresponding SPI, SPEI and PDSI
index values for each drought state in the proposed HMM framework—
near normal, moderate, severe and extreme droughts—are not
available, direct comparisons could not be made.
• Using the graphical model-based index, modeling of uncertainty in
crop water stress-based drought analysis is possible.
17
Comparison of Drought Indices
17
Results

18. 18Loc. id 7 :
41.25° N, 87.25°W
18
Results
Comparison of Drought Indices

19. 19
Results
Loc. id 35 :
39.25° N, 85.75° W
19
Comparison of Drought Indices

20. 20
Results
Drought state probabilities for Loc. id 7 at weekly time scale using HMM and data at 4 km
resolution at (a) loc id 7 and (b) loc id 35 respectively, for the period Jun 1987-May 1989
JUN 1987
JUN 1987
MAY 1989
MAY 1989
JAN 1988
JAN 1988
MAY 1988
MAY 1988
JAN 1989
JAN 1989
Temporal dependencies at weekly time scales exhibited by soil
moisture do not follow first order Markov property at one time step. A
more complex HMM framework is needed. However, with finer
temporal resolutions, information derived can be useful for planning
irrigation, drought monitoring and effective management of available
soil water.

21. Conclusions
• A probabilistic agricultural drought index based on crop water stress was
formulated within a graphical model framework, with hidden states
representing different drought categories
• Crop water stress was modeled using HMMs with a tridiagonal transition
matrix and beta emission densities to develop a probabilistic model based
on a bounded stress function.
• Drought severity category is defined differently for each location by the
HMM, and hence, an averaged or aggregated assessment for a region
cannot be considered accurate.
21
21

22. Conclusions
• The transition trend among drought states is not similar at all places in
Indiana. Results tend to be site-specific, suggesting the need for advanced
regionalization studies for regional agricultural drought outlook.
• Comparison of indices indicated that many of drought events during
dominant crop growing season (May-October) that were not identified by the
SPI, SPEI and SC-PDSI, were revealed by the proposed index.
• Drought analysis based on weekly time series data are more useful in
irrigation scheduling and soil water management. However, temporal
dependencies at weekly time scale require more complex HMMs.
22

23. THANK YOU
23