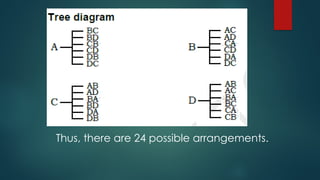
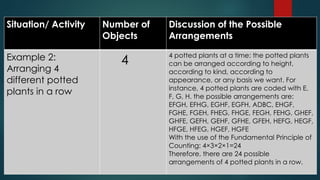
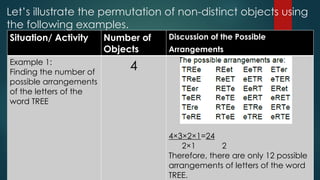
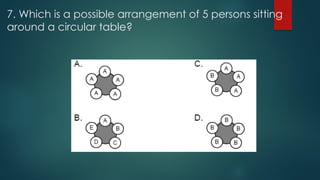
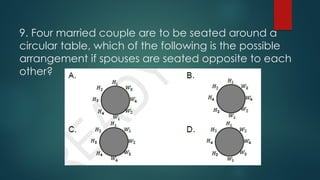
The document outlines techniques for counting permutations of objects, including making tables, tree diagrams, systematic listing, and the fundamental principle of counting. It discusses permutations of distinct and non-distinct objects, providing examples and exercises that illustrate these concepts. Additionally, it covers circular permutations and their application in arranging objects in a circular manner.

1. Illustrating
Permutation of
Objects
LESSON 1 – ILLUSTRATING THE PERMUTATION OF DISTINCT OBJECTS

2. Four Techniques in Counting Events
 Making a table is a technique where values or different
possibilities are tabulated.
 Tree diagram is another technique which uses line segments
originating from an event to an outcome. This is a picture of all
possible outcomes when an event is unfolded.
 Systematic listing is a counting technique that involves a
complete list of all possible outcomes.
 Fundamental Principle of Counting is a counting technique in
which if two events are independent and one event occurs in a
ways, and the other event occurs in b ways, then, these events
occur in ab ways.

3. Try this!
There are 4 cyclists in a race. In how many ways
will they be ranked as first, second, and third
placers?
 Making a table

4. Thus, there are 24 possible arrangements.

5.  Systematic listing
There are only four cyclists: A, B, C and D. There are four
cyclists to choose from for the first place, three cyclists
to choose from for the second place and two cyclists
to choose from for the third place.
 The actual list of all possible arrangements is ABC,
ABD, ACB, ACD, ADB, ADC, BAC, BAD, BCA, BCD,
BDA, BDC, CAB, CAD, CBA, CBD, CDA, CDB, DAB,
DAC, DBA, DBC, DCA, DCB.
 Therefore, there are 24 possible arrangements.

6. Fundamental Principle of Counting

7. Permutation
 A Permutation refers to the different arrangement of
objects in a definitive manner, in which the order of
the objects is important. There are two types of
permutations, permutations of objects in a line and
permutations of objects in a circle. Permutation of
distinct objects and permutation of non-distinct
objects are the two kinds of permutations of objects in
a line.

8. What is a permutation of distinct objects?
 A Permutation of distinct objects refers to the different
arrangements of distinct objects in a line. It is the different
arrangements when no objects are identical or the same.
Here are some examples:
1. Arranging 4 different potted plants in a row
- What makes this a permutation of distinct objects is that, 4 different
potted plants are distinct objects and are arranged in a line.
2. Getting the possible arrangements of letters of READ
- The four letters in READ are all distinct letters and are arranged in a
line.
3. Choosing a president, a vice president, a secretary and a
treasurer from the 12 members in a club

9. Let’s illustrate the permutation of distinct objects
using a different set of examples.
Situation/ Activity Number of
Objects
Discussion of the Possible
Arrangements
Example 1:
Arranging 3
different
mathematics books
in a shelf
3
3 books at a time:
Suppose the three different mathematics
books have titles, Algebra, Geometry, and
Statistics. Let us code them with letters A, G,
S respectively.
The possible arrangements are:
AGS, ASG, GSA, GAS, SAG, SGA
With the use of the Fundamental Principle of
Counting: 3×2×1=6
Thus, there are 6 possible arrangements of
mathematics books in a shelf.

10. Situation/ Activity Number of
Objects
Discussion of the Possible
Arrangements
Example 2:
Arranging 4
different potted
plants in a row
4
4 potted plants at a time: the potted plants
can be arranged according to height,
according to kind, according to
appearance, or any basis we want. For
instance, 4 potted plants are coded with E,
F, G, H. the possible arrangements are:
EFGH, EFHG, EGHF, EGFH, ADBC, EHGF,
FGHE, FGEH, FHEG, FHGE, FEGH, FEHG, GHEF,
GHFE, GEFH, GEHF, GFHE, GFEH, HEFG, HEGF,
HFGE, HFEG, HGEF, HGFE
With the use of the Fundamental Principle of
Counting: 4×3×2×1=24
Therefore, there are 24 possible
arrangements of 4 potted plants in a row.

11. Situation/ Activity Number of
Objects
Discussion of the Possible
Arrangements
Example 3:
Electing a
Mathematics club
president, vice-
president and a
secretary from 10
members
10 (Note: It’s hard making a list of
all possible arrangements when
the list is long)
The number of possible
outcomes for the different
position is given below:
President- 10 possible choices
Vice President- 9 possible
choices
Secretary- 8 possible choices

12. Situation/ Activity Number of
Objects
Discussion of the Possible
Arrangements
Example 4:
Getting the possible
arrangement of
letters that could
be the anagram of
the word BREAK
5 An Anagram is a word or
phrase created by
rearranging all the letters of
a certain word. The letters
must be used only once
and the word that is formed
has meaning.

13. Activity 1: Am I Distinct or Not?
Directions: Write Distinct if the activity/situation illustrates a permutation
of distinct objects and write Not, if it does not.
1. Shoe is the anagram for hose.
2. She arranges 6 potted plants in a row.
3. One possible arrangement of CREAM is MARCE.
4. The letters of the word MATH can be arranged into 24 ways.
5. He selected 2 leaders from the 5 members in the group.
6. 3551 is an odd four-digit PIN of Shirley’s mobile phone.
7. Marvin won the “suertres lotto” combination in the PCSO game.
8. The customer chooses 2 vegetable dishes from a menu of 6.
9. They used different digits as PIN to unlock the mobile phone.
10. The librarian arranges 8 different mathematics books in a shelf.

14. 11. The saleslady displays 5 the same rubber shoes on the display
rack.
12. The cashier opens a vault with different digits of combination
lock.
13. Mrs. Cruz can hang her 3 different photo frames in a row on
the wall in 6 ways.
14. The teacher chooses two men and 3 women to form a
committee from 10 people.
15. The 4 ladies arranged themselves in a row for picture taking.

15. Activity 2: Fill Me In
Directions: Read each statement below and fill in the blank with the correct
answer. (Note: answers may be more than one word)
1. ______________ refers to the different arrangement of objects in a definitive
manner.
2. There are two types of permutations of objects in a line. These are
_____________________ and _______________________.
3. _____________________ refers to the number of arrangements of distinct objects.
4. In permutation of distinct objects, the objects are not _______________.
5. The four _________________ helps to illustrate permutation of objects. The counting
techniques such as ________________, _________________, __________________ and
__________________ help to describe and count the number of possible
arrangement of objects.

16. Activity 3: Find Ways!
Directions: Read, understand and answer the problem below.
Problem: Vice Ganda is a well-known artist. Suppose he is
planning to have a concert tour in the following four cities –
Davao, Cagayan de Oro, Malaybalay and Valencia, list and
count the number of ways he can arrange his possible tour
schedules.

17. Lesson 2: Illustrating the Permutation of
Non-Distinct Objects
 Activity 4: Find My Anagram
Directions: Rearrange the letters of the following words and
find the possible arrangement of these letters that could be
the anagrams of the words below:
1. Free 4. Cheaper 7. Deeper
10. Importunate
2. Vases 5. Petitioner 8. Pleases
3. Peels 6. Output 9. Stressed

18. Permutation of Non-distinct Objects
 It is another type of permutation in a line in which objects are not
distinct or not unique.
Here are some examples:
1. Arranging the letters of the word MATHEMATICS.
- This permutation is non-distinct because there is duplication of
letters. There are 2 M’s, 2 A’s and 2 T’s.
2. 5 vases of the same kind and 3 candle stands of the same kind
are arranged in a line.
- This is a permutation of non-distinct objects because there are
objects to be arranged in a line that are alike or the same.

19. Let’s illustrate the permutation of non-distinct objects using
the following examples.
Situation/ Activity Number of
Objects
Discussion of the Possible
Arrangements
Example 1:
Finding the number of
possible arrangements
of the letters of the
word TREE
4
4×3×2×1=24
2×1 2
Therefore, there are only 12 possible
arrangements of letters of the word
TREE.

20. Example 2:
Displaying 5 flags in which 3 are red and 2 are
yellow
Example 3:
Assigning the same feed to 3 pigs and
another feed to 3 pigs

21. Activity 5: True or False
Directions: Write TRUE if the statement is true and write FALSE if it is
otherwise.
1. 10589 is the 5- non-distinct digit PIN of my phone.
2. DIVIDE is the anagram for DIVISION.
3. There are 7 ways to write in order, the word “ARRANGE.”
4. One possible arrangement of ADD is DAD.
5. WHEREVER is a permutation of non-distinct objects.
6. EVERYWHERE is not a permutation of non-distinct objects.
7. It takes 100 ways to arrange the letters of the word LETTER.
8. One possible arrangement of the letters of the word
MULTIPLICATION is MULTIPLY.
9. There are 12 possible arrangements of letters of the word ROOM.
10. 5 persons lining up, does not involve permutation of non-distinct
objects.

22. 11. The objects to be arranged in permutation of non-distinct
objects are unique.
12. Getting the anagram of BUTTER is an example of permutation of
non-distinct objects.
13. Permutation of non-distinct objects is a different arrangement
where objects are not distinct.
14. You can form 180 different words with or without meaning if you
rearrange the letters of the word BETTER.
15. Putting 3 plates of the same design and 3 glasses of the same
size in a row on the table involves permutation of non-distinct
objects.

23. Activity 6: What Am I?
Directions: Read each statement below and fill in the
blank with the correct answer. (Note: answers may be
more than one word)
1. Permutation of non-distinct objects is another type of
____________________.
2. It is a permutation when objects are _________________.
3. Rearranging the letters of the word CELLPHONE is an
example of permutation of ________________.
4. The digits 1-3-3-1-2 can be arranged into ___ ways.
5. The possible arrangement of the letters of the word
LETTERS with meaning is _____________.

24. Activity 7: Line it up!
Directions: Read, understand and answer the problem
below.
Problem: The covered court of Kitaotao National High
School is to be lined up with flags. In how many ways that
the 10 flags can be arranged if there are 5 blue, 3 red
and 2 white flags?

25. Lesson 3: Illustrating the Circular
Permutation of Objects
Activity 8: Possible Arrangement
Directions: Read, understand and answer the
problem below.
Problem: Joelle has 3 guests, A, B and C. She needs
to arrange them around a circular table. What are
the possible arrangements?

26. A Circular permutation is a type of
permutation where the different objects are
arranged in a circular manner.
Here are some examples:
1. 3 people are seated around a circular table.
2. 5 different keys are arranged in a key ring.
3. 6 different beads on a bracelet

27. Let’s find out how to illustrate the circular permutation of
objects given another set of examples.
Situation/ Activity Number of
Objects
Discussion of the Possible
Arrangements
Example 1:
3 people are
seated sitting
around a circular
table
3
Suppose the 3 people are A, B and C.
Observe the following illustrations.

28. Situation/ Activity Number of
Objects
Discussion of the Possible
Arrangements
Example 2:
4 campers
sitting around a
campfire
4 Suppose the campers are A, B, C and D.
The possible arrangements of 4 campers
are:

29. Directions: Read each question carefully and choose the letter
that corresponds to the correct answer.
1. What do you call a permutation when the arrangement of
objects is in circular pattern?
A. Circle permutation C. Permutation of distinct
objects
B. Circular permutation D. Permutation of non-distinct
objects
2. Which situation illustrates a circular permutation?
A. 5 persons stood in a line
B. 5 persons are seated in a row
C. 5 different plates are arranged at a round table
D. None of the above

30. 3. The following do not illustrate circular permutation EXCEPT
A. 8 different keys arranged in a key ring
B. Arranging the letters, A, B and C in a row
C. 7 women arranged themselves for a picture taking
D. None of the above
4. Which of the following is an example of a circular
permutation?
A. 10 children stood in a circle to play a game
B. 5 plates in a circular shape are placed on the table
C. 5 different circular picture frames are hanged on the wall
D. All of the above

31. 5. Below are situations involving circular permutation EXCEPT
A. 10 charms are arranged on a bracelet
B. 6 campers are arranged around a campfire
C. 4 different circular cakes are displayed on the table
D. 3 different ash trays are arranged around a circular side
table
6. What is a circular permutation? A. It is a type of
permutation.
B. The arrangement of objects is in circular manner.
C. There is no first place in the arrangement of objects in
circular permutation.
D. All of the above

32. 7. Which is a possible arrangement of 5 persons sitting
around a circular table?

33. 8. Three boys and three girls are to be seated around a dining
table. John is among the boys and does not like any girl to be
beside him. Just like John, Lovely does not like any boy beside
her. Which of the following could be a possible arrangement?

34. 9. Four married couple are to be seated around a
circular table, which of the following is the possible
arrangement if spouses are seated opposite to each
other?

35. 10. Below are the possible arrangements
of six campers around a campfire EXCEPT