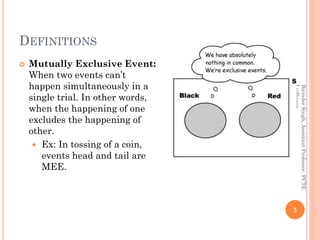
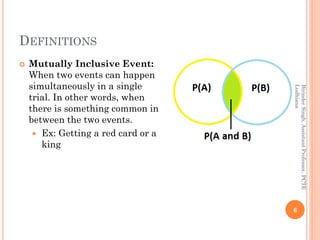
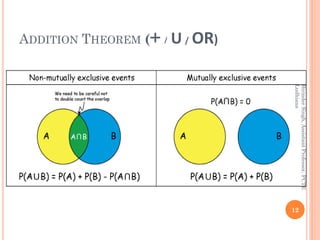
The document provides definitions and concepts related to probability, including experiments, events, complementary and mutually exclusive events, sample spaces, and the basic principles of calculating probabilities. It outlines various theorems such as the addition and multiplication theorems, along with practical problems for applying these concepts in real-world scenarios. Additionally, it addresses the use of Bayes' theorem and includes practice problems to reinforce the understanding of probability.

1. PROBABILITY

2. DEFINITIONS
 Experiment: When a trial is conducted to obtain some
statistical information.
 Ex: Tossing of a fair coin
 Ex: Rolling of a die
 Event: The possible outcomes of a trial, denoted by capital
letters A,B,C etc.
 Ex: In tossing of a coin, the outcomes – head or tail are
events.
 Equally Likely Events: The events are said to be equally
likely if the chance of happening of each event is equal or
same.
 Ex: In tossing of a coin, the events H or T are equally likely. 2
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

3. DEFINITIONS
 Favorable Events: The event which we are considering
for study.
 Ex: Getting a head in case of tossing a coin
 Ex: Getting a 6 in case of rolling a die
 Sample Space: The total number of possible outcomes
taken together. These are also called exhaustive events.
 Ex: The set of H,T in tossing a coin
 Ex: The set of 1,2,3,4,5,6 in rolling a die
3
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

4. DEFINITIONS
 Complementary Events are two outcomes of an
event that are the only two possible outcomes.
 Ex: flipping a coin and getting heads or tails. Head is
complement to tail.
 In rolling of a die, getting 1 or 2 are not
complementary events.
4
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

5. DEFINITIONS
 Mutually Exclusive Event:
When two events can’t
happen simultaneously in a
single trial. In other words,
when the happening of one
excludes the happening of
other.
 Ex: In tossing of a coin,
events head and tail are
MEE.
5
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

6. DEFINITIONS
 Mutually Inclusive Event:
When two events can happen
simultaneously in a single
trial. In other words, when
there is something common in
between the two events.
 Ex: Getting a red card or a
king
6
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

7. PROBABILITY
 It is the likeliness of any event i.e. what is the
chance that particular event will happen?
 Eg:
 What is the probability that CSK will win IPL 2018?
 What is the probability that it will rain today?
 What is the probability that after going through
these slides you understand Probability?
Probability = Favorable outcomes / Total outcomes
7
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

8. PRACTICE PROBLEMS
Q1: In case of rolling a die, what is the probability
of getting:
a) an even number
b) prime number
c) not even number
d) Number greater than 4
Q2: In a lottery, there are 10 prizes and 90 blanks.
If a person holds one ticket
a) an even number
b) prime number
c) not even number
8
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

9. PRACTICE PROBLEMS
Q3: In case of drawing a card, what is the
probability of getting:
a) an ace
b) Red card
c) Face card
d) Black king
Q4: What is the probability that a non leap year
selected at random will contain 53 Sundays?
Q5: What is the probability that a leap year
selected at random will contain 53 Sundays? 9
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

10. PRACTICE PROBLEMS
Q6: Two dice are thrown, what is the probability of
getting:
a) Sum of 11
b) Sum of 10
10
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

11. THEOREMS OF PROBABILITY
 Addition Theorem (For Mutually Exclusive & not
Mutually Exclusive)
 Multiplication Theorem (For Independent Events
& Dependent Events)
11
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

12. ADDITION THEOREM (+ / U / OR)
12
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

13. PRACTICE PROBLEMS
Q1: A card is drawn. What is the probability of getting
either a king or queen?
Q2: A bag contains 30 balls numbered 1 to 30. One ball
is drawn at random. Find the probability that the
number of the ball is
i. a multiple of 5 or 8
ii. a multiple of 3 or 4
Q3: An urn contains 4 red, 5 black, 3 yellow and 11
green balls. A ball is drawn at random. Find the
probability that:
i. It is either red, black or yellow ball
ii. It is either red, black, green or yellow ball 13
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

14. PRACTICE PROBLEMS
Q4: A card is drawn at random. What is the
probability that:
i. It is either a king or black card
ii. It is either an ace or club
14
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

15. DEFINITIONS

15
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

16. MULTIPLICATION THEOREM (X / ∩/ AND)
 If A and B are two independent events, then the
probability of the simultaneous occurrence of A and B is
equal to the product of their individual probabilities. i.e.
 P (A∩B) = P(A) . P(B)
 If A and B are two dependent events, then the probability
of the simultaneous occurrence of A and B is equal to the
probability of one event multiplied by the conditional
probability of the other event. i.e.
 P(A∩B) = P(A) . P(B/A)
16
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

17. PRACTICE PROBLEMS
Q1: A coin is tossed three times. What is the probability of
getting all the three heads? (1/8)
Q2: From a pack of 52 cards, two cards are drawn at random.
What is the probability that both cards are kings if :
i. Drawn with replacement (1/169)
ii. Drawn without replacement (1/221)
Q3: A bag contains 4 red balls, 3 white balls and 5 black balls.
Two balls are drawn one after the other. Find the probability
that the first is red and the second is black if:
i. Drawn with replacement (5/36)
ii. Drawn without replacement (5/33) 17
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

18. PRACTICE PROBLEMS
Q4: An electronic device is made of three components A, B and C.
The probability of failure of the component A, B & C is 0.01, 0.02
and 0.05 respectively. Find the probability that the device will
work satisfactorily. (0.92)
Q5: A person is known to hit the target in 3 out of 4 shots
whereas another person is known to hit the target in 2 out of 3
shots. Find the probability of the target being hit at all when
both of them try. (11/12)
Q6: A problem is given to three students A, B and C whose
chance of solving it are 1/2, 1/3 and ¼ respectively. What is the
probability that the problem will be solved? (3/4)
18
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

19. PRACTICE PROBLEMS
Q7: Four cards are drawn without replacement. What is the
probability that they are all aces? (1/270725)
Q8: A bag contains 5 white balls and 3 red balls, four balls are
successively drawn out and not replaced. What is the chance that
balls appear alternatively in color? (1/7)
Q9: Four cards are drawn without replacement. What is the
probability that:
i. They are of the same suit (44/4165)
ii. They are of different suits (2197/20825)
19
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

20. PRACTICE PROBLEMS
Q10: A can hit a target 4 times in 5 shots, B 3 times in 4 shots
and C twice in 3 shots. What is the probability that at least two
shots hit? (5/6)
Q11: Three coins are tossed simultaneously. What is the
probability that they will fall two heads and one tail? (3/8)
Q9: Four cards are drawn without replacement. What is the
probability that:
i. They are of the same suit (44/4165)
ii. They are of different suits (2197/20825)
20
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

21. PRACTICE PROBLEMS – BAYES’ THEOREM
 An insurance company insured 2000 scooter drivers, 4000 car
drivers and 6000 truck drivers. The probability of an accident
involving a scooter, a car and a truck are 0.01, 0.03 and 0.15
respectively. One of the insured persons meets with an accident.
What is the probability that he is a scooter driver? (1/52)
 A factory has two machines A and B. Past record shows that
machine A produced 60% of the items of output and machine B
produced 40% of the items. Further, 2% of the items produced by
machine A and 1% produced by machine B were defective. All
the items are put into one stockpile and then one item is chosen
at random from this and is found to be defective. What is the
probability that it was produced by machine B? (1/4)
21
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

22.  A coin is tossed three times, consider the following
events. A: ‘No head appears’, B: ‘Exactly one head
appears’ and C: ‘Atleast two heads appear’. Find their
probabilities.
 One card is drawn from a well shuffled deck of 52
cards. If each outcome is equally likely, calculate the
probability that the card will be
(i) a diamond (ii) not an ace (iii) a black card (iv) not a
diamond (v) not a black card.
 A bag contains 9 discs of which 4 are red, 3 are blue
and 2 are yellow. The discs are similar in shape and
size. A disc is drawn at random from the bag.
Calculate the probability that it will be (i) red, (ii)
yellow, (iii) blue, (iv) not blue, (v) either red or yellow.
22
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

23.  Two students Anil and Ashima appeared in an
examination. The probability that Anil will
qualify the examination is 0.05 and that Ashima
will qualify the examination is 0.10. The
probability that both will qualify the examination
is 0.02. Find the probability that
(a) Both Anil and Ashima will not qualify the
examination.
(b) Atleast one of them will not qualify the
examination and
(c) Only one of them will qualify the
examination. 23
BirinderSingh,AssistantProfessor,PCTE
Ludhiana

24.  A letter is chosen at random from the word
‘ASSASSINATION’. Find the probability that
letter is (i) a vowel (ii) a consonant
 Find the probability that when a hand of 7 cards
is drawn from a well shuffled deck of 52 cards, it
contains (i) all Kings (ii) 3 Kings (iii) atleast 3
Kings.
24
BirinderSingh,AssistantProfessor,PCTE
Ludhiana