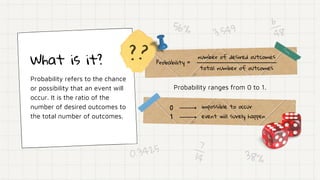
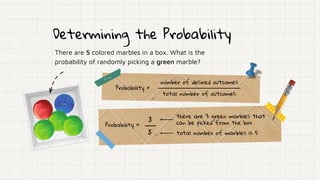
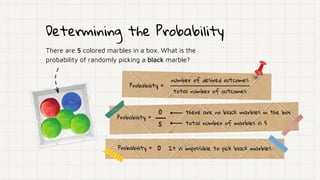
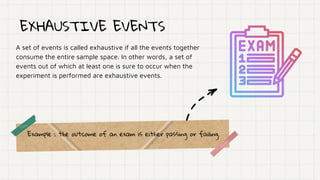
The document discusses different types of probability events: - Sure events have a probability of 1 and will always occur. Impossible events have a probability of 0. - Complementary events cover all possible outcomes such that one event must occur. - Mutually exclusive events cannot occur together, while mutually inclusive events can occur simultaneously. - Exhaustive events together cover all possible outcomes such that one is sure to occur. Equally likely events have outcomes that are equally possible. 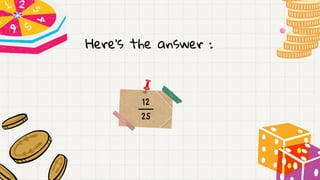- An example calculates the probability of randomly selecting a number greater than 13 from numbers 1 to 25. The probability is 12/25.

1. Probability - Type of
events
??
4
12
4
12
5.76
53%
53%
0.3425
53%
7.802

2. Lesson Outline
Here's an overview of today's
lesson.
Probability
Determining the probability
Types of events
3
15
0.645
74%
26%
0.3425

3. What is it?
Probability refers to the chance
or possibility that an event will
occur. It is the ratio of the
number of desired outcomes to
the total number of outcomes.
Probability =
number of desired outcomes
total number of outcomes
Probability ranges from 0 to 1.
0 impossible to occur
event will surely happen
1
??
7
14
3.549
38%
56%
0.3425
6
48

4. Probability =
number of desired outcomes
total number of outcomes
??
Probability =
1 only 1 marble is blue
total number of marbles is 5
5
There are 5 colored marbles in a box. What is the
probability of randomly picking a blue marble?
Determining the Probability

5. Determining the Probability
There are 5 colored marbles in a box. What is the
probability of randomly picking a green marble?
Probability =
number of desired outcomes
total number of outcomes
Probability =
there are 3 green marbles that
can be picked from the box
total number of marbles is 5
3
5

6. Determining the Probability
There are 5 colored marbles in a box. What is the
probability of randomly picking a black marble?
Probability =
number of desired outcomes
total number of outcomes
Probability =
there are no black marbles in the box
total number of marbles is 5
0
5
Probability = 0 It is impossible to pick black marbles.

7. 4
24
Sure event
Impossible event
Complementary event
Mutually exclusive event
Mutually inclusive event
Exhaustive event
Equally likely event
TYPES OF
EVENTS
0.6281
37%
32%
6.392

8. SURE EVENT
A sure event is one that will
always happen. The probability
of occurrence of a sure event
will always be 1. Example:the earth revolving around
the sun is a sure event.

9. IMPOSSIBLE EVENT
If the probability of occurrence of an event is zero,
then it is an impossible event.
Example: The event of getting 7 when a die
is thrown is impossible. This is because the
outcomes of the throwing a die include {1, 2,
3, 4, 5, 6}.

10. COMPLEMENTARY EVENT
For every event A, there corresponds another
event A is called the complementary event to
A. It is also called the event ‘not A’.
For example, on tossing a coin let E be defined as getting a head.
Then the complement of E is E' which will be the event of getting
a tail. Thus, E and E' together make up complementary events.

11. MUTUALLY EXCLUSIVE EVENTS
Events that cannot occur at the same time are
known as mutually exclusive events. Thus,
mutually exclusive events in probability do not
have any common outcomes.
Example :When we roll a die, the sample space S = {1,2,3,4,5,6}.
(i) Since{1, 3} {2, 4, 5, 6}= , ∩ ∅ t he events {1,3}and{2, 4,5,6}are
mutually exclusive events.

12. MUTUALLY INCLUSIVE EVENTS
Two events are mutually inclusive when they
can both occur simultaneously.
Example :When we roll a die, the sample space S = {1,2,3,4,5,6}.
(i) The events {2,3,5},{5,6} are mutually inclusive, since {2, 3, 5} {5,
6}= 5 ∩ ≠∅

13. EXHAUSTIVE EVENTS
A set of events is called exhaustive if all the events together
consume the entire sample space. In other words, a set of
events out of which at least one is sure to occur when the
experiment is performed are exhaustive events.
Example : the outcome of an exam is either passing or failing.

14. EQUALLY LIKELY EVENTS
Equally likely events in probability are those
events in which the outcomes are equally
possible.
For example, on tossing a coin, getting a head or getting a
tail, are equally likely events.

15. ??
3
10
5
15
Let's try:
A number from 1 to 25 is drawn at random.
What is the probability of getting a number
greater than 13?
0.645
64%
32%
0.3425
0.9785

16. 12
25
Here's the answer :

17. 2
27
4
12
0.3425
4
12
4.7219
53%
12%
39%
7.802
Thank you!