読書会で使ったスライド

1. PRML読書会@KMC
12章 連続潜在変数
@taki0313
2011/05/22
PRMl読書会@KMC-12章:連続潜在変数

2. お品書き
♣ 12.1 主成分分析(PCA)
♣ 12.2 確率的主成分分析(PPCA)
♣ 12.3 カーネル主成分分析(kPCA)
♣ 12.4 非線形潜在変数モデル
どうみても主成分分析の章です，ありがt(ry
PRMl読書会@KMC-12章:連続潜在変数

3. 背景とか，そういう感じのこと
- 主成分分析自体の背景
– データは完全に自由なわけではない
低次元の多様体の周辺に存在する
- この章は8章から始まってる潜在変数関係の話の最後です
- 線形ガウスモデル(8.1.4)を利用する
– 主成分分析(PCA)などの定式化が導かれる
PRMl読書会@KMC-12章:連続潜在変数 3/21

4. §12.1 主成分分析
- 主成分分析(PCA; Principal Component Analysis) / KL変換
– 機械学習系の研究テーマの柱の1つ
– 第4回IBISML研究会では...
確率的主成分分析における自動次元選択について
複数情報源に対する主成分分析
PRMl読書会@KMC-12章:連続潜在変数 4/21

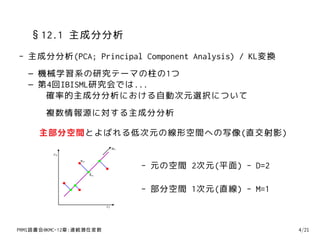
5. §12.1 主成分分析
- 主成分分析(PCA; Principal Component Analysis) / KL変換
– 機械学習系の研究テーマの柱の1つ
– 第4回IBISML研究会では...
確率的主成分分析における自動次元選択について
複数情報源に対する主成分分析
主部分空間とよばれる低次元の線形空間への写像(直交射影)
u1
x2
xn
- 元の空間 2次元(平面) - D=2
xn
- 部分空間 1次元(直線) - M=1
x1
PRMl読書会@KMC-12章:連続潜在変数 4/21

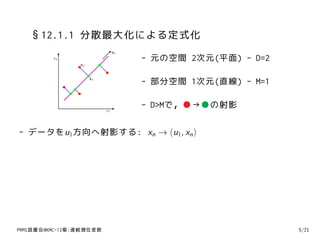
6. §12.1.1 分散最大化による定式化
u1
x2 - 元の空間 2次元(平面) - D=2
xn
xn
- 部分空間 1次元(直線) - M=1
x1
- D>Mで，●→●の射影
- データをu1方向へ射影する: xn → (u1, xn )
PRMl読書会@KMC-12章:連続潜在変数 5/21

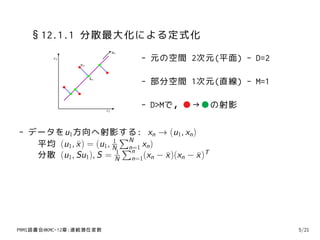
7. §12.1.1 分散最大化による定式化
u1
x2 - 元の空間 2次元(平面) - D=2
xn
xn
- 部分空間 1次元(直線) - M=1
x1
- D>Mで，●→●の射影
- データをu1方向へ射影する: xn → (u1, xn )
1
∑N
平均 (u1, x ) = (u1, N ∑ xn )
¯ n=1
n
分散 (u1, Su1), S = N n=1(xn − x )(xn − x )T
1
¯ ¯
PRMl読書会@KMC-12章:連続潜在変数 5/21

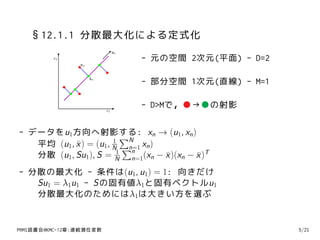
8. §12.1.1 分散最大化による定式化
u1
x2 - 元の空間 2次元(平面) - D=2
xn
xn
- 部分空間 1次元(直線) - M=1
x1
- D>Mで，●→●の射影
- データをu1方向へ射影する: xn → (u1, xn )
1
∑N
平均 (u1, x ) = (u1, N ∑ xn )
¯ n=1
n
分散 (u1, Su1), S = N n=1(xn − x )(xn − x )T
1
¯ ¯
- 分散の最大化 - 条件は(u1, u1) = 1: 向きだけ
Su1 = λ1u1 - Sの固有値λ1と固有ベクトルu1
分散最大化のためにはλ1は大きい方を選ぶ
PRMl読書会@KMC-12章:連続潜在変数 5/21

9. §12.1.2 誤差最小化による定式化
∑D
- 正規直交基底 {ui }, i = 1, 2, ... D より， xn = i=1 αni ui
∑D
(xn , uj ) = αnj → xn = i=1(xn , ui )ui
PRMl読書会@KMC-12章:連続潜在変数 6/21

10. §12.1.2 誤差最小化による定式化
∑D
- 正規直交基底 {ui }, i = 1, 2, ... D より， xn = i=1 αni ui
∑D
(xn , uj ) = αnj → xn = i=1(xn , ui )ui
- 次元を削減するためにD次元のうち，M < D次元だけを使う
∑M ∑D
xn → xn = i=1 zni ui + i=M+1 bi ui
˜
∑
歪み度 J = N 1
||xn − x ||2 → minimize
¯
zni = (xn , ui ) i = 1, ... , M, bi = (¯ , ui ) i = 1, ... , M
x
PRMl読書会@KMC-12章:連続潜在変数 6/21

11. §12.1.2 誤差最小化による定式化
∑D
- 正規直交基底 {ui }, i = 1, 2, ... D より， xn = i=1 αni ui
∑D
(xn , uj ) = αnj → xn = i=1(xn , ui )ui
- 次元を削減するためにD次元のうち，M < D次元だけを使う
∑M ∑D
xn → xn = i=1 zni ui + i=M+1 bi ui
˜
∑
歪み度 J = N 1
||xn − x ||2 → minimize
¯
zni = (xn , ui ) i = 1, ... , M, bi = (¯ , ui ) i = 1, ... , M
x
∑D
- xn − xn = i=M+1(xn − x , ui )ui なので
˜ ¯
∑N ∑D
J = N n=1 i=M+1{(xn , ui ) − (¯ , ui )}2 を最小化する
1
x
∑D
J = i=M+1(ui , Sui ) 変形した
§12.1.1の逆を行う → 小さい固有値の方からD-M個
- 小さい固有値の部分は近似しちゃってもいいよ!
PRMl読書会@KMC-12章:連続潜在変数 6/21

12. §12.1.1-2 は似たようなことを言ってる
- 上手く近似するために，大きい方から選ぼう
- 近似しても影響ないように，小さい方を切ろう
Mean λ1 = 3.4 · 105 λ2 = 2.8 · 105 λ3 = 2.4 · 105 λ4 = 1.6 · 105
Original M =1 M = 10 M = 50 M = 250
PRMl読書会@KMC-12章:連続潜在変数 6/21

13. §12.1.3 主成分分析の応用
- 誤差最小化の時の式をこねこね
∑M ∑D
xn = x + i=1((xn , ui ) − (¯ , ui ))ui ← x = i=1(¯ , ui )ui
˜ ¯ x ¯ x
データの圧縮法を表現している (D→M)
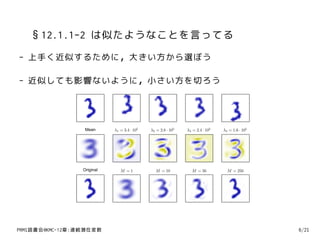
PRMl読書会@KMC-12章:連続潜在変数 7/21

14. §12.1.3 主成分分析の応用
- 誤差最小化の時の式をこねこね
∑M ∑D
xn = x + i=1((xn , ui ) − (¯ , ui ))ui ← x = i=1(¯ , ui )ui
˜ ¯ x ¯ x
データの圧縮法を表現している (D→M)
- 簡単な標準化(正規化?) - 平均0，分散1にする
- PCAはより完全な(本格的な)正規化が可能 - 平均0,共分散Iにする
白色化(whitening) / 球状化(sphereing)
1
−2 T
yn = L U (xn − x )
¯
PRMl読書会@KMC-12章:連続潜在変数 7/21

15. §12.1.4 高次元データに対する主成分分析
- データ数NのD次元データをM次元に射影する (M < D)
- (?)N点は高々N − 1次元の線形の部分空間を定義するから...
N − 1 < Mはダメ(意味がないらしい)
対応する固有値が0になることに対応するらしい(足りない分)
固有ベクトルとか求めてO(D 3)
PRMl読書会@KMC-12章:連続潜在変数 8/21

16. §12.1.4 高次元データに対する主成分分析
- データ数NのD次元データをM次元に射影する (M < D)
- (?)N点は高々N − 1次元の線形の部分空間を定義するから...
N − 1 < Mはダメ(意味がないらしい)
対応する固有値が0になることに対応するらしい(足りない分)
固有ベクトルとか求めてO(D 3)
( )
- X = (x1 − x ) (x2 − x ) ... (xN − x ) : NxD行列
T ¯ ¯ ¯
1
S = NXTX
1
→ N X T Xui = λi ui , i = 1, 2, ...
1
→ N XX T (Xui ) = λ(Xui ), vi = Xui とする
1
→ N XX T vi = λi vi
- 元の共分散行列と同じ固有値λi を持ち，D → N， O(N 3)
PRMl読書会@KMC-12章:連続潜在変数 8/21

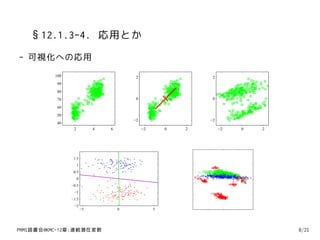
17. §12.1.3-4. 応用とか
- 可視化への応用
100 2 2
90
80
70 0 0
60
50
−2 −2
40
2 4 6 −2 0 2 −2 0 2
1.5
1
0.5
0
−0.5
−1
−1.5
−2
−5 0 5
PRMl読書会@KMC-12章:連続潜在変数 8/21

18. §12.2 確率的主成分分析(1)
- 主成分分析 x ベイズ = 確率的主成分分析(PPCA)
制約付きのガウス分布に基づく
確率的取り扱いをするので，ベイズの定理/EM法が使える
生成モデルとして利用できる
その他にもいいこといっぱい(?)
- データ→主成分を探す ⇀ 裏に隠れ変数がある→データ
↽
p(z) = N (z | 0, I )
p(x|z) = N (x | Wz + µ, σ 2I )
§8.1.4: 線形ガウスモデルの例(全部ガウス!)
∫
周辺確率 p(x) = p(x|z)p(z)dz
PRMl読書会@KMC-12章:連続潜在変数 9/21

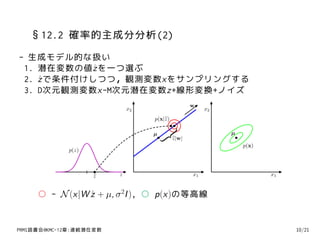
19. §12.2 確率的主成分分析(2)
- 生成モデル的な扱い
1. 潜在変数の値ˆ を一つ選ぶ
z
2. z で条件付けしつつ，観測変数xをサンプリングする
ˆ
3. D次元観測変数x-M次元潜在変数z+線形変換+ノイズ
w
x2 x2
p(x|z)
µ µ
z|w|
}
p(x)
p(z)
z z x1 x1
○ - N (x|W z + µ, σ 2I ), ○ p(x)の等高線
ˆ
PRMl読書会@KMC-12章:連続潜在変数 10/21

20. §12.2 確率的主成分分析(2)
- 生成モデル的な扱い
1. 潜在変数の値ˆ を一つ選ぶ
z
2. z で条件付けしつつ，観測変数xをサンプリングする
ˆ
3. D次元観測変数x-M次元潜在変数z+線形変換+ノイズ
- 設定: 裏に主成分(に対応する隠れ変数があるんじゃね?)
p(z) = N (z | 0, I ), p(x|z) = N (x | Wz + µ, σ 2I )
∫
p(x) = p(x|z)p(z)dz, これらをごにょごにょして処理する
- ガウス分布同士の積なので - E[x] = µ, Cov[x] = WW T + σ 2I
- 生成モデルから考えて x = Wz + µ + ϵ → 計算でも同じ
- p291. 直感的には... → 意味不明
PRMl読書会@KMC-12章:連続潜在変数 10/21

21. §12.2 確率的主成分分析(2)
- 設定: 裏に主成分(に対応する隠れ変数があるんじゃね?)
p(z) = N (z | 0, I )
p(x|z) = N (x | Wz + µ, σ 2I )
∫
p(x) = p(x|z)p(z)dz = N (x | µ, C )
E[x] = µ
Cov[x] = WW T + σ 2I
˜
- W は直交行列Rに関して回転不変(冗長) - W = WR
˜ ˜
W W T = WW T ,
- 逆行列 C −1 = σ −2I − σ −2WM −1W T , M = W T W + σ 2I
- 事後分布p(z | x) = N (z | M −1W T (x − µ), σ 2M −1)
PRMl読書会@KMC-12章:連続潜在変数 10/21

22. §12.2.1 最尤法による主成分分析
- 例によってデータの集合X = {x1, ... , xN } + 最尤法
∑
N
ln p(X | µ, W , σ 2) = ln p(xn | W , µ, σ 2)
i=1
1∑
D
ND N
= − ln(2π) − ln |C | − (xn − µ)C −1(xn − µ)T
2 2 2 n=1
- µでの微分=0より，µ = x になる - 今までのガウス分布の推定と同じ
¯
N
ln p(X | µ, W , σ 2) = − {D ln(2π) + ln |C | + Tr (C −1S)}
2
- σ, W についてはもっと複雑
PRMl読書会@KMC-12章:連続潜在変数 11/21

23. §12.2.1 最尤法による主成分分析
- WML = UM (LM − σ 2I )1/2R
Rは直交行列，UM はDxM行列-列ベクトルがSの固有ベクトル
LM 対応する固有値の対角行列
M個の固有ベクトルを上位M個取ってくると(尤度)最大化される
このときW が通常の主成分分析の主部分空間を成す
(√ )
λ1 − σ 1
2u
(√ ) (√ )
( ) λ1 − σ 2 λ1 − σ 1 √ 0
2u
u1 u2 √ 0 =
0 λ2 − σ 2 0 λ 2 − σ 2 u2
PRMl読書会@KMC-12章:連続潜在変数 11/21

24. §12.2.1 最尤法による主成分分析
1
∑D
- 2
σML= i=M+1 λi
D −M
下位の切り捨てられた分の分散を表す
- 主成分分析は固有ベクトルの方向に分散λi を与える
λi − σ 2: 潜在変数空間の分布→Wの空間へ射影する
σ 2: ノイズ
- お話略
PRMl読書会@KMC-12章:連続潜在変数 11/21

25. §12.2.1 最尤法による主成分分析
- 共分散行列: C = WW T + σ 2I
- (v , v ) = 1の向きを考える
(v , v ) = 1の向きには,分散λi = (v , Cv )を与える
v は主部分空間以外の固有ベクトルの一次結合とする
(v , U) = 0 → (v , Cv ) = σ 2
主部分空間に直交する方向でのノイズ
- v = ui を考える - (v , Cv ) = λi − σ 2 + σ 2 = λi
PRMl読書会@KMC-12章:連続潜在変数 11/21

26. §12.2.1 最尤法による主成分分析
- 最尤法によるモデルの構築の手法
共分散行列の固有値と固有ベクトルを利用する→W , σ 2を求める
- 仮にM = Dのとき(圧縮しないとき)
UM = U, LM = L, C = S
- PCAの定式化とPPCAの定式化は結局同じようなもん
p(z|x)の方向で圧縮操作を考える
E[z|x] = M −1WML(x − x ), M = W T W + σ 2I
T
¯
σ 2 → 0のとき(WMLWML)−1WML(x − x )
T T
¯
主部分空間への射影になるらしい(演習12.11)
- パラメータ数について
PRMl読書会@KMC-12章:連続潜在変数 11/21

27. §12.2.2 EMアルゴリズムによる主成分分析
- EM法の扱い(完全データと不完全データ...)
∑N
ln p(X , Z |µ, W , σ ) = n=1{ln p(xn |zn ) + ln p(zn )}
2
p(xn |zn )とp(zn )を実際に代入してガリガリ...
式ぇ...
- Eステップ - 古いパラメータで期待値を計算
E[zn ] = M −1W T (xn − x )
¯
E[zn zn ] = σ 2M −1 + E[zn ]E[zn ]T
T
- Mステップ - 最大化する(C.24 とかいろいろ使うらしい)
∑ ∑
Wnew = [ (xn − x )E[zn ] ][ E[zn zn ]]−1
¯ T T
σML ぇ...
2
PRMl読書会@KMC-12章:連続潜在変数 12/21

28. §12.2.2 EMアルゴリズムによる主成分分析
- EM法の利点がそのまま適応される - 反復処理
- 実は計算効率が良く，σ 2 → 0のとき，処理が簡単化
( )
E[zn zn ]の計算が不要, データ行列X
T ˜ ，Ω = ... E[zn ] ...
Eステップ: Ω = (Wold Wold )−1Wold X T
T T ˜
Mステップ: Wnew = X T ΩT (ΩΩT )−1
˜
PRMl読書会@KMC-12章:連続潜在変数 13/21

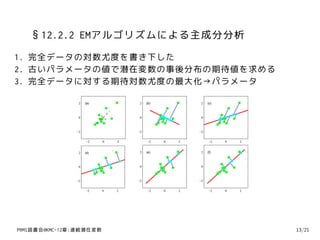
29. §12.2.2 EMアルゴリズムによる主成分分析
1. 完全データの対数尤度を書き下した
2. 古いパラメータの値で潜在変数の事後分布の期待値を求める
3. 完全データに対する期待対数尤度の最大化→パラメータ
2 (a) 2 (b) 2 (c)
0 0 0
−2 −2 −2
−2 0 2 −2 0 2 −2 0 2
2 (d) 2 (e) 2 (f)
0 0 0
−2 −2 −2
−2 0 2 −2 0 2 −2 0 2
PRMl読書会@KMC-12章:連続潜在変数 13/21

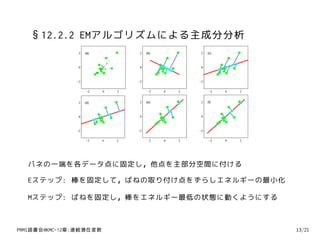
30. §12.2.2 EMアルゴリズムによる主成分分析
2 (a) 2 (b) 2 (c)
0 0 0
−2 −2 −2
−2 0 2 −2 0 2 −2 0 2
2 (d) 2 (e) 2 (f)
0 0 0
−2 −2 −2
−2 0 2 −2 0 2 −2 0 2
バネの一端を各データ点に固定し，他点を主部分空間に付ける
Eステップ: 棒を固定して，ばねの取り付け点をずらしエネルギーの最小化
Mステップ: ばねを固定し，棒をエネルギー最低の状態に動くようにする
PRMl読書会@KMC-12章:連続潜在変数 13/21

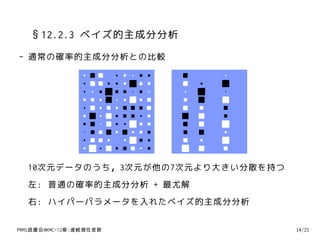
31. §12.2.3 ベイズ的主成分分析
- 今まではMを決めてた
可視化ならM=2だし，固有値がはっきり分かれるならそのあたり
- ベイズ的取り扱いをしたのでMが決まるはずだ
例えば交差確認法
ベイズ的取り扱いでモデル選択する
- モデルのパラメータµ, W , σ 2を消す → 難しい
- エビデンス近似に基づく手法
W の列ベクトルにパラメータαi を入れる
αi の値を周辺尤度関数の最大化で見い出す
有限のαi の数が有効な主部分空間の次元
PRMl読書会@KMC-12章:連続潜在変数 14/21

32. §12.2.3 ベイズ的主成分分析
- 通常の確率的主成分分析との比較
10次元データのうち，3次元が他の7次元より大きい分散を持つ
左: 普通の確率的主成分分析 + 最尤解
右: ハイパーパラメータを入れたベイズ的主成分分析
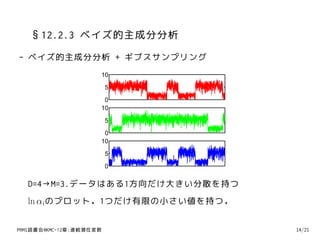
PRMl読書会@KMC-12章:連続潜在変数 14/21

33. §12.2.3 ベイズ的主成分分析
- ベイズ的主成分分析 + ギブスサンプリング
10
5
0
10
5
0
10
5
0
D=4→M=3.データはある1方向だけ大きい分散を持つ
ln αi のプロット．1つだけ有限の小さい値を持つ．
PRMl読書会@KMC-12章:連続潜在変数 14/21

34. §12.2.4 因子分析
- 観測変数xの条件付き分布の共分散が非等方的で対角的Ψ
- p(x|z) = N (x | Wz + µ, Ψ)
Ψ: 観測変数の座標毎に独立な分散を表現
W の列ベクトルに変数間の共分散が入っている
- このときp(x) = N (x|µ, C ), C = WW T + Ψ
- 閉じた解にならないので反復的に解く...
Eステップ & Mステップ(略)
個人的に思うこと→EM法をPPCAに導入しておくと
似た枠組みで因子分析と一緒に扱える(形も似てるし)
いろんな所にベイズの取り扱いを入れるのは
それらの分野の道具で無理矢理解くためだということか
PRMl読書会@KMC-12章:連続潜在変数 15/21

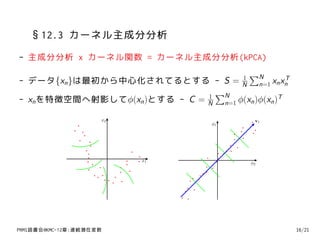
35. §12.3 カーネル主成分分析
- 主成分分析 x カーネル関数 = カーネル主成分分析(kPCA)
∑N
- データ{xn }は最初から中心化されてるとする - S = N n=1 xn xn
1 T
1
∑N
- xn を特徴空間へ射影してϕ(xn )とする - C = N n=1 ϕ(xn )ϕ(xn )T
x2 v1
ϕ1
x1
ϕ2
PRMl読書会@KMC-12章:連続潜在変数 16/21

36. §12.3 カーネル主成分分析
- C の固有値...を，Sと同じように行っていく
1
∑N
Cvi = λi vi より N n=1 ϕ(xn )(ϕ(xn ), vi ) = λi vi
∑N
よってλi > 0を仮定して vi = n=1 ain ϕ(xn )
- vi の展開を固有ベクトルの方程式に戻す
1
∑N T
∑N ∑N
N n=1 ϕ(xn )ϕ(xn ) n=1 ain ϕ(xn ) = λi n=1 ain ϕ(xn )
1
∑N ∑N ∑N
- N n=1 ϕ(xn )ϕ(xn )
T
n=1 ain ϕ(xn ) = λi n=1 ain ϕ(xn )
- 両辺にϕ(xl )T を掛け，カーネル関数k(xn , xm ) = (ϕ(xn ), ϕ(xm ))を使う
1
∑K ∑N ∑N
N n=1 k(xl , xn ) m=1 aim k(xn , xm ) = λi n=1 ain k(xl , xn )
- 行列表記らしい: K 2ai = λi NKai
PRMl読書会@KMC-12章:連続潜在変数 16/21

37. §12.3 カーネル主成分分析
- 行列表記らしい: K 2ai = λi NKai
ai は次元列ベクトル, 各要素ain .
Kai = λi Nai の固有方程式を解く ∑ ∑N N
規格化条件: 1 = (vi , vi ) = n=1 m=1 ain aim (ϕ(xn ), ϕ(xm ))
= (ai , Kai ) = λi N(ai , ai )
- 点xの固有ベクトルiの上への射影 - カーネル関数で求まる
∑N
yi (x) = (ϕ(x), vi ) = n=1 ain k(x, xn )
カーネル主成分分析 NxN行列K の固有値分解
カーネル法のアイデア (xi , xj ) → (ϕ(xi ), ϕ(xj ))
PRMl読書会@KMC-12章:連続潜在変数 16/21

38. §12.3 カーネル主成分分析
- 補足: 写像されたデータ集合ϕ(xn )の平均が0ではない
平均を引く(中心化?)の操作もϕ, kを使って定式化したい
˜ n ) = ϕ(xn ) − 1 ∑N ϕ(xl )
- ϕ(x N l=1
- K˜ = (ϕ(xn ), ϕ(xm ))...
nm
˜ ˜
˜
- K = K − 1N K − K 1N + 1N K 1N
1
1N はすべての要素が N である行列
- 通常の主成分分析(PCA)はk(xn , xm ) = (xn , xm )で再現
PRMl読書会@KMC-12章:連続潜在変数 16/21

39. §12.3 カーネル主成分分析
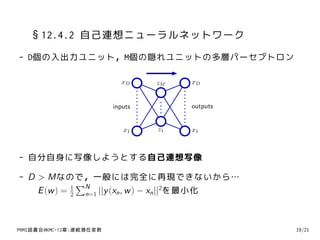
PRMl読書会@KMC-12章:連続潜在変数 16/21

40. §12.4 非線形潜在変数モデル
- §12.1-12.3 線形ガウス分布に基づくモデル
- §12.4 非ガウス的 or 非線形 or その両方に拡張する
- 非ガウス と 非線形の関係
ガウス分布 + 非線形の変数変換 → 一般的な分布 らしい
- ここからお話だけだよ
PRMl読書会@KMC-12章:連続潜在変数 17/21

41. §12.4.1 独立成分分析
- 独立成分分析(ICA; Independent Component Analysis)
∏M
潜在変数の分布がp(z) = j=1 p(zj )に分解されてる
e.g. 未知音源分離
- (線形の)主成分分析,因子分析では回転不変性がある
˜
W = WRと回転させても同じ結果になる
分離とかできないし…
PRMl読書会@KMC-12章:連続潜在変数 18/21

42. §12.4.2 自己連想ニューラルネットワーク
- D個の入出力ユニット，M個の隠れユニットの多層パーセプトロン
xD zM xD
inputs outputs
x1 z1 x1
- 自分自身に写像しようとする自己連想写像
- D > Mなので，一般には完全に再現できないから…
∑N
E (w ) = 2 n=1 ||y (xn , w ) − xn ||2を最小化
1
PRMl読書会@KMC-12章:連続潜在変数 19/21

43. §12.4.2 自己連想ニューラルネットワーク
- 隠れユニットが線形の活性化関数を持つとき
大局的な最適化を持ち，主成分分析と一致する
- 非線形の隠れユニットを使っても一緒
- 追加の隠れ層が使える場合
F1 F2
xD xD
inputs outputs
x1 x1
non-linear
PRMl読書会@KMC-12章:連続潜在変数 19/21

44. §12.4.2 自己連想ニューラルネットワーク
- 追加の隠れ層が使える場合: 2つの写像F1, F2の適用と見る
- D次元→M次元部分空間への写像 & M次元部分空間→D次元
x3 z2 x3
F1
F2
S
x1 z1 x1
x2 x2
- 非線形の主成分分析を行える
- 誤差関数の最小化問題に変わる
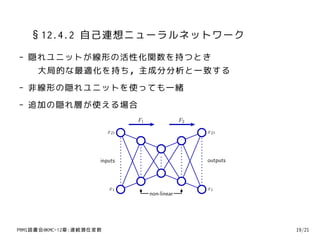
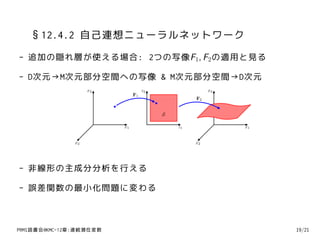
PRMl読書会@KMC-12章:連続潜在変数 19/21

45. §12.4.3 非線形多様体のモデル化
- 高次元データはより低次の非線形多様体に対応する
要するにたくさんの次元の数ほど自由度がない
1. 区分線形近似を組合せた多様体の表現
各部分で共通のコスト関数の最適化しつつ処理
2. 確率的主成分分析を混合する + EM
3. ベイズ的主成分分析 + 変分推論
4. 線形モデル→非線形モデル
通常のPCA(線形部分空間)→非線形の曲面上に射影
主成分曲線，主成分曲面，主成分超曲面… → むずい
PRMl読書会@KMC-12章:連続潜在変数 20/21

46. §12.4.3 非線形多様体のモデル化
- 可視化手法としてのPCA
多次元尺度構成法(MDS)
-- 2個のデータ点間の距離をなるべく保存するように
距離行列の固有ベクトルを求めることで低次元射影を見出す
非計量多次元尺度構成法(nonmetric MDS)
-- 距離行列→類似度行列
- ノンパラメトリックな次元削減と可視化
局所線形埋め込み(LLE)
等長特徴写像(isomap)
PRMl読書会@KMC-12章:連続潜在変数 20/21

47. §12.4.3 非線形多様体のモデル化
- 潜在特性モデル
潜在変数が連続，観測変数が離散の場合
上手く周辺化できなくなって，対策が必要らしい
- 密度ネットワーク
ガウス分布+非線形変換で任意の分布を構成できる性質
非線形性 ∼ 多層ニューラルネットワーク
潜在変数の周辺化ができない ∼ サンプリング
- 非線形関数の制限+潜在変数の分布を適切に選択
学習効率と非線形性を両立する
GTM 格子状に配置された有限個のデルタ関数で
定義される潜在変数の分布を用いる．
非線形写像は線形回帰モデル．
PRMl読書会@KMC-12章:連続潜在変数 20/21

48. §12.4.3 非線形多様体のモデル化
- PCAによる可視化(左) / GTMによる可視化(右)
- GTMは自己組織化マップ(SOM)の確率化版
PRMl読書会@KMC-12章:連続潜在変数 20/21

49. まとめ
- §12.1 PCAは主部分空間への写像: データ→部分空間
- §12.2 PPCAによる確率的な扱い
潜在変数→データ
尤度，EM法などが応用できる
- §12.3 kPCA - (x, y ) → (ϕ(x), ϕ(y ))
- §12.4 いろいろ話題がありますね(棒
まだまだ最新の研究がされてます(おわり)
PRMl読書会@KMC-12章:連続潜在変数 21/21