More Related Content
What's hot
PDF
PDF
PPTX
PDF
PDF
PDF
PDF
PDF
PPTX
PDF
PDF
PDF
基礎からのベイズ統計学 輪読会資料 第4章 メトロポリス・ヘイスティングス法 PDF
PDF
PDF
PDF
PDF
PPTX
PDF
PPTX
StanとRでベイズ統計モデリング読書会(Osaka.stan) 第6章 Viewers also liked
PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Bishop prml 11.5-11.6_wk77_100606-1152(発表に使った資料) PDF
Similar to PRML輪読#11
PDF
PPTX
PDF
PPTX
PPTX
PDF
PDF
PDF
Prml Reading Group 10 8.3 PDF
[DL輪読会]Deep Learning for Sampling from Arbitrary Probability Distributions PDF
[DL輪読会]Deep Learning 第17章 モンテカルロ法 PDF
Bishop prml 10.2.2-10.2.5_wk77_100412-0059 PPTX
PDF
PDF
PDF
PDF
Monte Carlo Methods (Chapter 17 in Deep learning by Ian Goodfellow) PDF
PRML Chapter 11 (11.0-11.2) PDF
Recently uploaded
PPTX
socialization in fundamentals of sociology.pptx PDF
Seminar midterm presentation by Chihana Usui PDF
Bases especialista admen rrhh minedu.pdf PDF
ПЛАН_профілактика правопорушень02.09.25.pdf PDF
ПОЛОЖЕННЯ_протидія насильству_підписане.pdf PDF
ПЛАН_навчально_профілактичні_заходи_запобігання_негативним_проявам.pdf PDF
ГРАФІК ГУРТКОВОЇ РОБОТИ 2025 kg72 grafik PRML輪読#11
- 1.
- 2.
「第11章 サンプリング法」の概要
• サンプリング法を⾏う⽬的
–ある関数𝑓(𝑧)の確率分布p(𝑧)のもとでの期待値を評価すること
• サンプリング法の発想
– 確率分布p(𝑧)から独⽴に抽出されたサンプルの集合z(')を得ることで,以下で期待値を
近似計算できる
• 対象の確率分布p(𝑧)から,サンプルの集合z(')
をどのように得るか(サンプリ
ング法)を今回整理する
2
- 3.
- 4.
- 5.
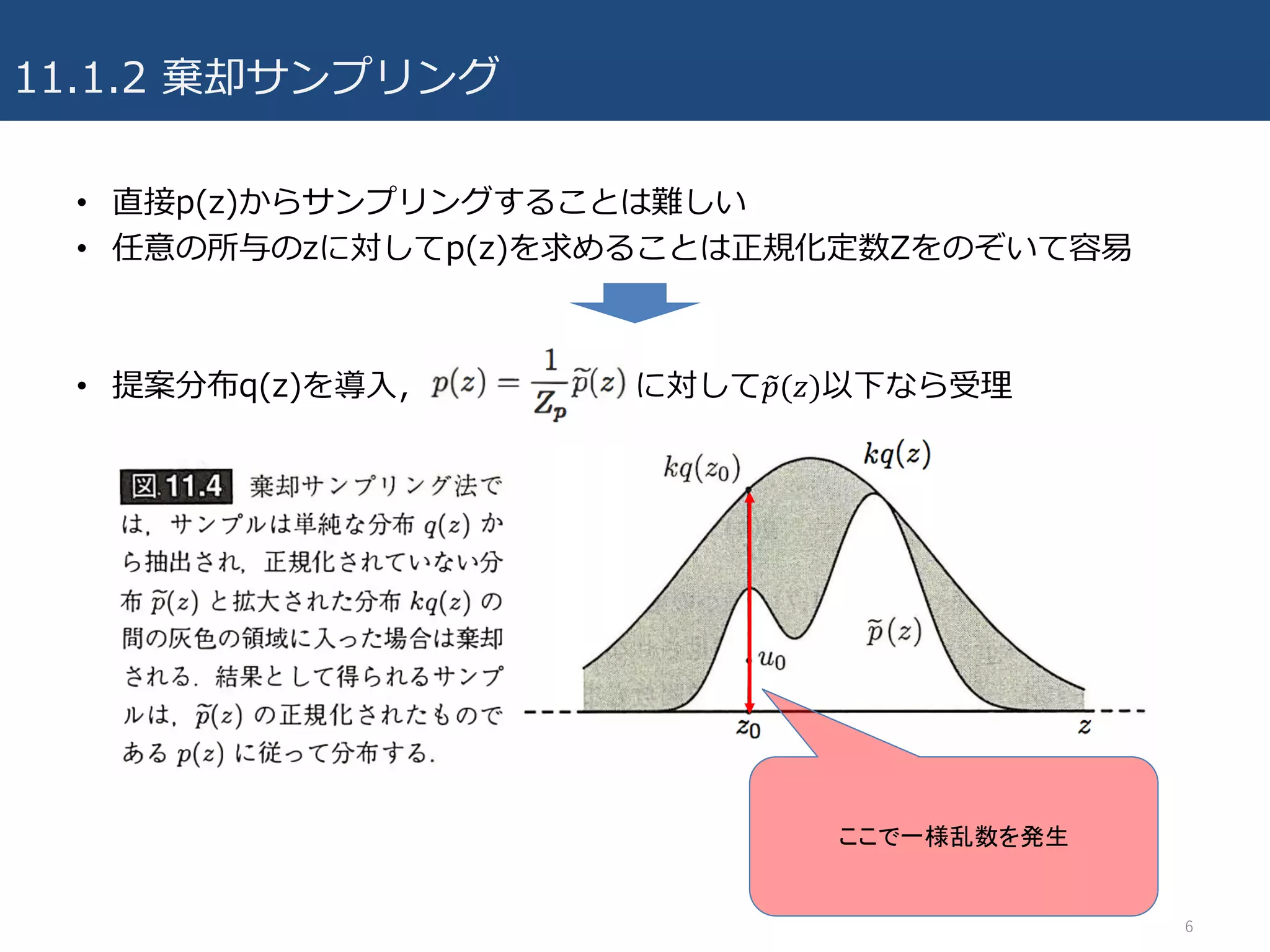
- 6.
- 7.
- 8.
11.1.4 重点サンプリング
• 重点サンプリングの概要
–サンプリングの⽬的は(11.1)の期待値を知ること->サンプリング⽅法ではなく、直接
期待値を求める⽅法
– 任意のzの値についてp(z)は容易にもとまるという前提
– 提案分布からサンプリングを抽出し,重要度で重み付けする
• 重点サンプリングの問題
– いくらでも⼤きな誤差のある結果を⽣み出す可能性があるが、それを防いだり知る指標
がない
8
重要度重み:求めたいものと異なる
分布からサンプリングされることに
よって生じるバイアスを包囲する
- 9.
- 10.
11.2 マルコフ連鎖モンテカルロ
• 「標準的なサンプリングアルゴリズム」では,⾼次元空間において重⼤な制
約があった
•マルコフ連鎖モンテカルロ(MCMC)を導⼊
• 現在の状態𝑧(/)
の記録を保持し,提案分布を現在の状況によって定義する
𝑞(𝑧|𝑧(/)
) =>サンプルの系列はマルコフ連鎖をなす
• 例:Metropolis アルゴリズム
1. 提案分布 𝑞(𝑧|𝑧∗) から𝑧∗ をサンプリングする
2. 以下の確率を計算
3. (0, 1)の⼀様分布からuを発⽣させる
4. uとAとの⽐較で,Aの⽅が⼤きければ𝑧45, = 𝑧∗と更新
- 𝑝(𝑧/)が増加するなら𝑧∗を必ず採択,そうでなくても減少率に応じて採択,更新する
10
- 11.
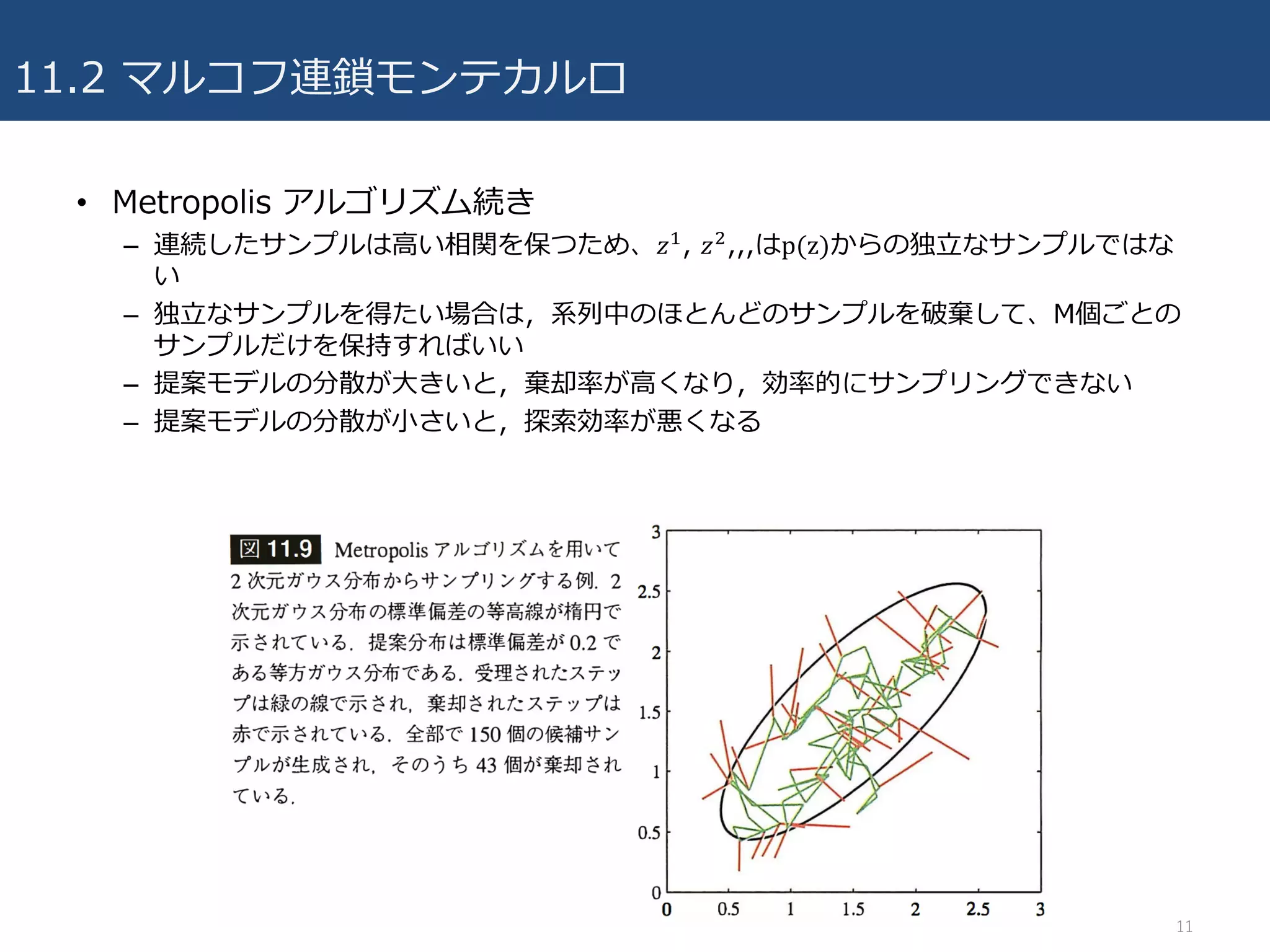
11.2 マルコフ連鎖モンテカルロ
• Metropolisアルゴリズム続き
– 連続したサンプルは⾼い相関を保つため、𝑧,, 𝑧6,,,はp(z)からの独⽴なサンプルではな
い
– 独⽴なサンプルを得たい場合は,系列中のほとんどのサンプルを破棄して、M個ごとの
サンプルだけを保持すればいい
– 提案モデルの分散が⼤きいと,棄却率が⾼くなり,効率的にサンプリングできない
– 提案モデルの分散が⼩さいと,探索効率が悪くなる
11
- 12.
11.2 マルコフ連鎖モンテカルロ
• ランダムウォーク
–初期状態がz7 = 0なら,
• 𝐸 𝑧/ = 0, 𝐸 𝑧/6
=
/
6
• 移動距離が時間の平⽅根に⽐例
– ランダムウォークは状態空間を探索するのに⾮効率
– ランダムウォーク的な振る舞いを避けることが,マルコフ連鎖モンテカルロ法の重要な
課題
12
- 13.
11.2.1 マルコフ連鎖
• マルコフ連鎖
–現在の状態は⼀つ前の過去の状態にしか依存しない
– 遷移確率を
で定義すると,以下のような場合に分布が不変(定常)である(どのステップにおいても
状態zʼからzへの遷移確率は同じ)
– 不変であるための⼗分条件(詳細釣り合い条件) =>可逆
– 初期分布の選択に関わらず,分布が求めたい不変分布𝑝∗(𝑧)に収束することも必要で,エ
ルゴード性を保つことが求められる
• どの状態から始めても,すべての状態に到達可能
13
- 14.
11.2.2 Metropolis-Hastings アルゴリズム
•Metropolis アルゴリズムを⼀般化したもの
– Metropolis アルゴリズムは対象な分布を想定していた
1. 提案分布 𝑞(𝑧|𝑧∗) から𝑧∗ をサンプリングする
2. 以下の確率を計算
3. (0, 1)の⼀様分布からuを発⽣させる
4. uとAとの⽐較で,Aの⽅が⼤きければ𝑧45, = 𝑧∗と更新
14
- 15.
- 16.
- 17.
11.3 ギブスサンプリング
• ギブスサンプリングの注意点
–エルゴード性
• 演習問題11.12
• エルゴード性が満たされない(どこからでも,どこへでも)
場合に,ギブスサンプリングは使えない
– ランダムウォーク
• ランダムウォーク的な振る舞いを低減させるために,過剰緩和を⾏う
• 𝛼が0の時は普通のギブスサンプリング-> −1 < 𝛼 < 1とすることで過剰緩和を⾏う
• 変数が⾼い相関を保つ場合に状態空間内での⽅向付けられた移動を促進する
17
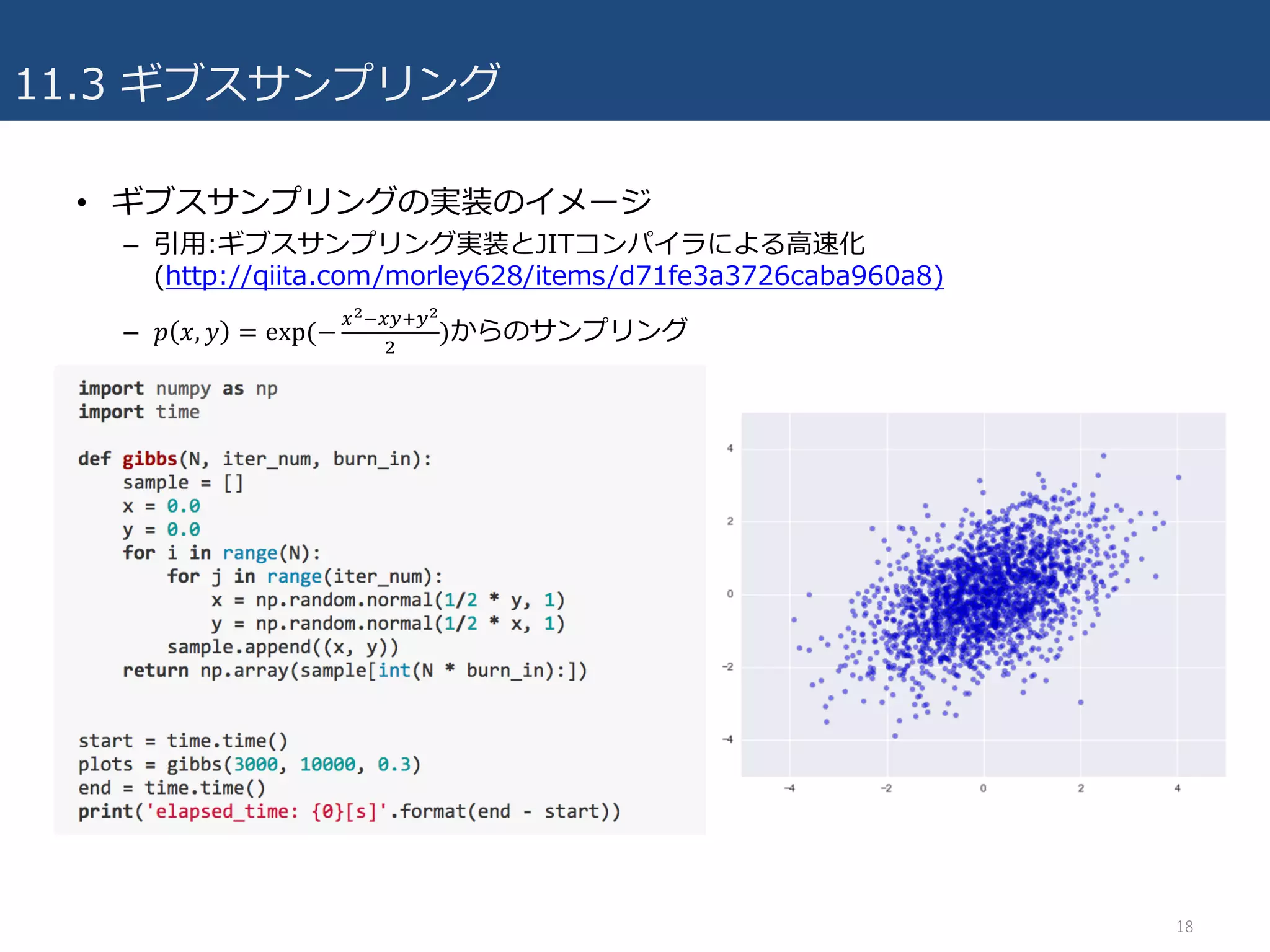
- 18.
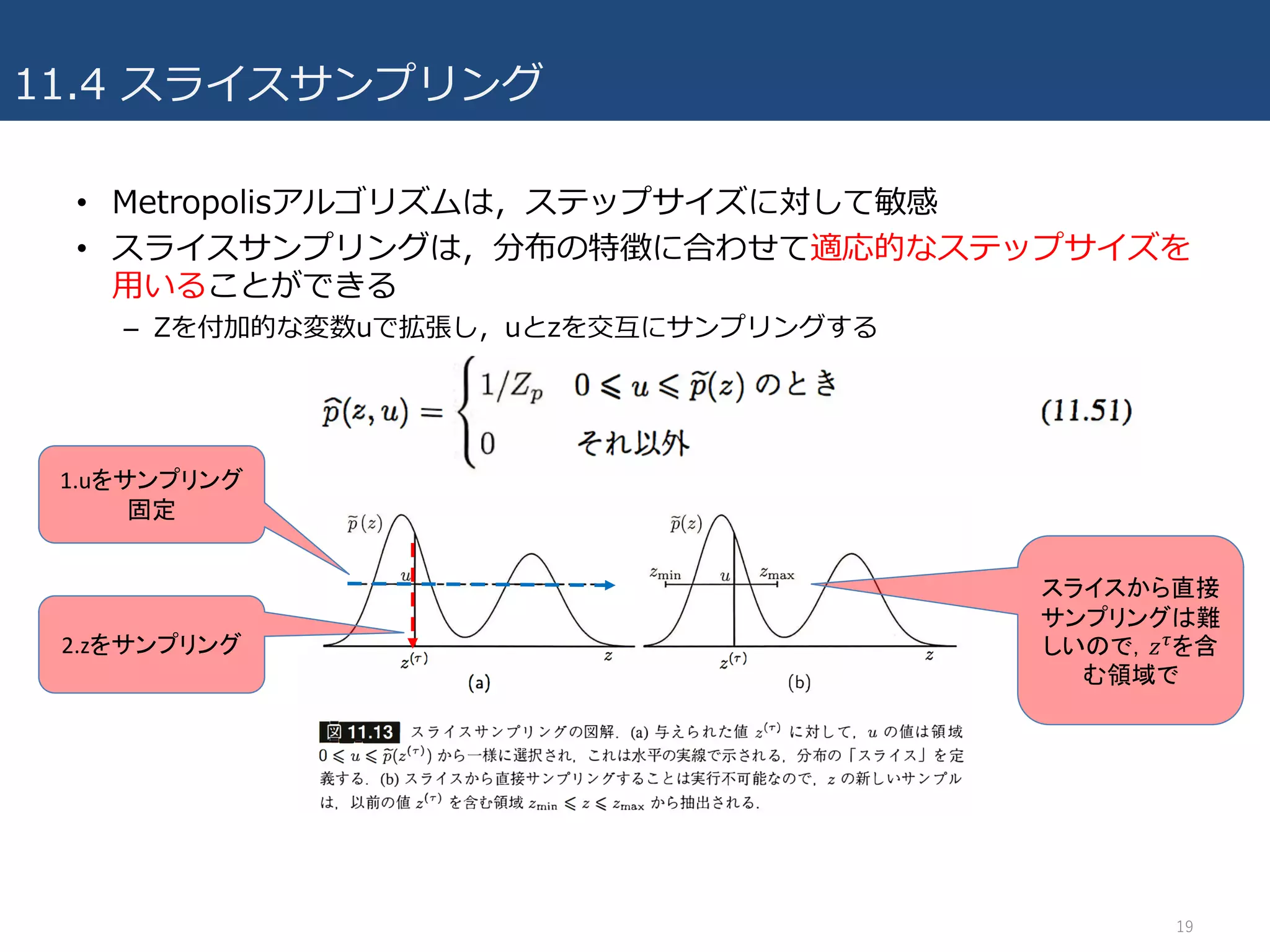
- 19.
- 20.
- 21.
- 22.
11.5.1 ⼒学系
• 全エネルギーがハミルトン関数である位相空間の上での同時分布を考える
1.ハミルトン関数は時間発展において⼀定
2. 位相空間の体積が保存されるリューヴィルの定理)
であることを⽤いて,
– ハミルトン⼒学がp(z, r)を不変にすることが導かれる
– z, r は値が変化するので,ハミルトン⼒学を有限の時間区間で積分すれば,ランダム
ウォーク的な振る舞いを避けて,系統的な⽅法でzに⼤きな変化を起こすことができる
– エルゴード的なサンプリングをするためには,位相空間での追加的な移動を導⼊する
(ex: rの値をzを条件とする分布から抽出したものに置き換えるなど)
– リューヴィルの定理が成り⽴つようにハミルトン⼒学を積分する必要がある
• =>リープフロッグ離散化(リープフロッグの更新と周辺分布からの運動量変数の再サンプリ
ングを交互に⾏う)
22
- 23.
- 24.
11.6 分配関数の推定
• 今までのサンプリングでは確率分布の正規化定数𝑍Hは知る必要がなかっ
た
– モデルエビデンス(モデルが与えられた時の観測データの確率)を知りたい(ベイズの枠
組みで⽐較したい)時に,𝑍Hを知りたい
– ⽐較においては,2つのモデルの分配関数の⽐がわかれば良い
– 重点サンプリングを⽤いて,分布𝑝Iが解析的に計算できれば, 𝑍Hも特定可能
– JK
JL⁄ が⼤きな変動をしない場合に有効だが,実際には解析的に求められる適した𝑝Iを⾒
つけることは困難.=>マルコフ連鎖から得られたサンプリングから𝑍Iを決める
24
- 25.
参考・引⽤資料
• パターン認識と機械学習 下
–C.M. ビショップ (著), 元⽥ 浩 (監訳), 栗⽥ 多喜夫 (監訳), 樋⼝ 知之 (監訳), 松本 裕
治 (監訳), 村⽥ 昇 (監訳)
• 研究室内PRML勉強会 11章2-4節(Koji Matsuda, SlideShare)
– https://www.slideshare.net/koji_matsuda/prml-1124
• 第11章 サンプリング法(原 祐輔, powerpoint)
– http://bin.t.u-tokyo.ac.jp/prml2009/
• ギブスサンプリング実装とJITコンパイラによる⾼速化(Qiita, morley628)
– http://qiita.com/morley628/items/d71fe3a3726caba960a8
25