This document discusses the relationship between control as inference, reinforcement learning, and active inference. It provides an overview of key concepts such as Markov decision processes (MDPs), partially observable MDPs (POMDPs), optimality variables, the evidence lower bound (ELBO), variational inference, and the free energy principle as applied to active inference. Control as inference frames reinforcement learning as probabilistic inference by defining a generative process and performing variational inference to find an optimal policy. Active inference uses the free energy principle and minimizes expected free energy to select actions that resolve uncertainty.

1. 2020/11/02
1

2. !
! control as inference active inference
!
!
!
! Christopher L Buckley
!
!
!
2
! On the Relationship Between Active Inference and Control as Inference [Millidge+ 20] Control as inference active inference
! Active inference: demystified and compared [Sajid+ 20] Active inference
! Reinforcement Learning and Control as Probabilistic Inference: Tutorial and Review [Levine 18] Control as inference
! Reinforcement Learning as Iterative and Amortised Inference [Millidge+ 20] Control as Inference amortized
! What does the free energy principle tell us about the brain? [Gershman 19] Active inference
! Hindsight Expectation Maximization for Goal-conditioned Reinforcement Learning [Tang+ 20] Control as inference Variational RL

3. MDP
! MDP
! state action
state transition probability
! MDP
t st ∈ 𝒮 at ∈ 𝒜 t + 1
st+1 p (st+1 |st, at)
3
st−1 st st+1
at−1 at at+1

4. POMDP
! MDP observation
!
! POMDP
s o
o s p(o|s)
4
st−1 st st+1
at−1 at at+1
ot−1 ot ot+1

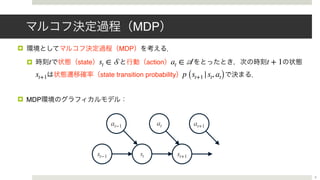
5. ! MDP policy
! trajectory
!
! reward
!
p (a|s)
T τ = (s1, a1, . . . , sT, aT)
r (st, at)
𝔼p(τ)
[
T
∑
t=1
r (st, at)
]
popt (a|s)
5
p(τ) = p(s1:T, a1:T) =
T
∏
t=1
p(at |st)p(st |st−1, at−1)

6. ! plan
!
! Active inference
!
!
!
π = [a1, . . . , aT]
T τ = (s1:T, π)
π
6
p(τ) = p(π)p(s1:T |π) = p(π)
T
∏
t=1
p(st |st−1, π)

7. ! preference
?
1.
! Control as inference RL as inference Planning as inference
! Variational RL
2.
!
! active inference
7

8. Control as Inference Variational RL
8

9. ! optimality variable
!
!
=>
𝒪t ∈ {0,1}
t st at 𝒪t = 1 t
r
9
p(𝒪t = 1|st, at) := exp (r (st, at))
st
𝒪t
at
st+1
𝒪t+1
at+1
st−1
𝒪t−1
at−1

10. !
! optimal trajectory distribution
! p ( 𝒪1:t |τ)
10
p ( 𝒪1:T |τ) =
T
∏
t=1
p ( 𝒪t |st, at) =
T
∏
t=1
exp (r (st, at))
p (τ| 𝒪1:T) =
p ( 𝒪1:T |τ) p (τ)
p ( 𝒪1:T)
popt(τ) = p (τ| 𝒪1:T)
※ p ( 𝒪1:T = 1) = p ( 𝒪1:T)

11. !
!
!
!
p (τ| 𝒪1:T) ∝ p ( 𝒪1:T |τ) p (τ)
𝒪1:T
τ
q(τ)
q(τ)
11
̂q = arg min
q
DKL [q(τ)∥p (τ| 𝒪1:T)]
τ
𝒪1:t
p (τ| 𝒪1:T) ≈ q(τ)
p (τ)
p ( 𝒪1:T |τ)

12. ELBO
! ELBO
! ELBO
! ELBO
!
q(τ) p(τ)
12
log p ( 𝒪1:T) = log
∫
p ( 𝒪1:T, τ) dτ
= log 𝔼q(τ)
[
p ( 𝒪1:T, τ)
q (τ) ]
≥ 𝔼q(τ) [log p ( 𝒪1:T |τ) + log p (τ) − log q (τ)]
= 𝔼q(τ)
[
T
∑
t=1
r (st, at)
]
− DKL [q(τ)∥p(τ)] =: L(q)
τ
𝒪1:t
p (τ| 𝒪1:T) ≈ q(τ)
p (τ)
p ( 𝒪1:T |τ)

13. 1.
!
!
!
!
!
control as inference; CAI
p (at ∣ st) =
1
| 𝒜|
qϕ (at ∣ st) ϕ
13
qϕ(τ) :=
T
∏
t=1
qϕ (at ∣ st) q (st ∣ st−1, at−1) =
T
∏
t=1
qϕ (at ∣ st) p (st ∣ st−1, at−1)
p(τ) :=
T
∏
t=1
p (at ∣ st) p (st ∣ st−1, at−1) =
1
| 𝒜|
T
∏
t=1
p (st ∣ st−1, at−1)

14. 1.
! ELBO
!
!
14
L(ϕ) = 𝔼qϕ(τ)
[
T
∑
t=1
r (st, at)
]
− DKL [qϕ(τ)∥p(τ)]
≥ 𝔼qϕ(τ)
[
T
∑
t=1
r (st, at) − log qϕ(at |st)
]
= 𝔼qϕ(τ)
[
T
∑
t=1
r (st, at) + ℋ (qϕ(at |st))]
J(ϕ) := 𝔼qϕ(τ)
[
T
∑
t=1
r (st, at) + ℋ (qϕ(at |st))]

15. Soft Actor-Critic
! Soft Actor-Critic SAC [Haarnoja+ 17, 18]
! ELBO off-policy .
! Q
! Q critic actor
!
! Control as Inference https://deeplearning.jp/reinforcement_cource-2020s/
! Control as Inference https://www.slideshare.net/DeepLearningJP2016/dlcontrol-as-inference-201266247
Qθ (st, at) = r(st, at) + 𝔼p(st+1|st,at) [V(st+1)]
Qθ (st, at) qϕ(at |st)
15
Jq
t (ϕ) = 𝔼qϕ(at|st)p(st) [
log (qϕ (at |st)) − Qθ (st, at)]
JQ
t (θ) = 𝔼qϕ(at|st)p(st)
[(
r (st, at) + 𝔼p(st+1|st,at) [V¯θ (st+1)] − Qθ (st, at))
2
]
Vθ(st+1) = 𝔼qϕ(at+1|st+1) [Qθ(st+1, at+1) − log qϕ(at+1 |st+1)]
Q

16. POMDP
! Control as inference POMDP
! VAE
16
! SLAC[Lee+ 19]
! RNN
!
! [Han+ 19]
! RNN VRNN[Chung+ 16]
! variational recurrent model VRMat

17. CAI
! CAI
! Mirror descent [Bubeck, 14]
=> Variational Inference Model Predictive Control VI-MPC [Okada+ 19]
!
π
𝒲(π) = 𝔼q(τ)[p(𝒪1:T |τ)]
p(𝒪1:T |τ) := f(r(τ))
17
q(i+1)
(π) ←
q(i)
(π) ⋅ 𝒲 (π) ⋅ q(i)
(π)
𝔼q(i)(π) [ 𝒲 (π) ⋅ q(i) (π)]
[Okada+ 19]

18. Control as inference
! CAI
! SAC VI-MPC
! amortized [Kingma+ 13]
! [Millidge+ 20]
! amortized
18

19. 2.
! CAI
! ELBO
! ELBO
!
=> Variational RL
p (at ∣ st)
q θ
19
pθ(τ) :=
T
∏
t=1
pθ (at ∣ st) p (st ∣ st−1, at−1)
L(θ, q) = 𝔼q(τ)
[
T
∑
t=1
r (st, at)
]
− DKL [q(τ)∥pθ(τ)]

20. EM
! E
!
! M
! E ELBO
!
! MPO[Abdolmaleki+ 18] V-MPO[Song+ 19]
! M E
θ θ = θold
θ
θ
20
̂θ = max
θ
𝔼q(τ)[log pθ(τ)] = max
θ
𝔼q(τ)
[
T
∑
t=1
log pθ (at ∣ st)
]
q(τ) = pθold (τ| 𝒪1:T) =
p ( 𝒪1:T ∣ τ) pθold
(τ)
∑τ
p ( 𝒪1:T ∣ τ) pθold
(τ)

21. MPO E
! Maximum a posteriori Policy Optimization MPO [Abdolmaleki+ 18]
!
! E Q
! Q off-policy
! MPO DL
! https://www.slideshare.net/DeepLearningJP2016/dlhyper-parameter-agnostic-methods-in-reinforcement-learning
θold pθold
(at ∣ st) ̂Qθold
(st, at)
21
q(τ) =
T
∏
t=1
q (at ∣ st) p (st ∣ st−1, at−1)
q(at |st) ∝ pθold
(at ∣ st)exp
̂Qθold
(st, at)
η
η > 0

22. Control as inference Variational RL
! Control as inference
! Variational RL
!
22
τ
𝒪1:T
p (τ| 𝒪1:T) ≈ q(τ)
p (τ)
p ( 𝒪1:T |τ)
τ
𝒪1:T
pθ (τ| 𝒪1:T) ≈ q(τ)
pθ (τ)
p ( 𝒪1:T |τ)
θ
Control as inference Variational RL

23. active inference
23

24. !
! Friston
!
!
24
※ ver.3
https://www.slideshare.net/masatoshiyoshida/ss-238982118

25. !
!
!
!
! unconscious inference
!
!
!
!
25
?
要因結果
推論（知覚）

26. !
!
!
o s
o s
26
p(o, s) = p(o|s)p(s)
p(s|o) =
p(s)p(o|s)
∑s
p(s)p(o|s)
推論
状態
⽣成
観測
内部モデル
（世界モデル）環境
!
"
o s

27. !
!
! Bayesian surprise
! active learning
!
!
a o a
u(o) = DKL[p(s ∣ o, a)||p(s ∣ a)] I(a)
a
I(a) a s o
I(a)
27
I(a) :=
∑
o
p(o ∣ a)DKL[p(s ∣ o, a)||p(s ∣ a)] = 𝔼p(o∣a)[u(o)]

28. !
.
!
!
o1:T π = [a1, . . . , aT]
U(o1:T) =
T
∑
t=1
u (ot)
28
I(π) = 𝔼p(o1:T∣π) [U(o1:T)] =
∑
o1:T
p(o1:T ∣ π)U(o1:T)

29. !
! ELBO
! ELBO variational free energy
! free energy principle
!
!
q(s)
−log p(o)
29
log p(o) ≥ 𝔼q(s) [
log
p(o, s)
q(s) ]
F(o, q) := − 𝔼q(s) [
log
p(o, s)
q(s) ]

30. !
!
!
! 1
!
!
! 2
o
−log p(o)
q
q(s)
30
F(o, q) = − log p(o) + DKL[q(s)||p(s|o)]

31. ! POMDP
!
!
!
!
π = [a1, . . . , aT]
31
p(o1:T, s1:T |π) =
T
∏
t=1
p(ot |st)p(st |st−1, π)
q(s1:T |π) =
T
∏
t=1
q(st |π)
F(o1:T, π) = − 𝔼q(s1:T|π)
[
log
p(o1:T, s1:T |π)
q(s1:T |π) ]
st−1 st st+1
at−1 at at+1
ot−1 ot ot+1
π

32. !
! expected free energy
32
G(π):= 𝔼p(o1:T ∣ s1:T, π) [F (o1:T, π)]
= − 𝔼p(o1:T ∣ s1:T, π)
𝔼q(s1:T |π)
[
log
p (o1:T, s1:T |π)
q (s1:T |π) ]
= − 𝔼q(o1:T, s1:T |π)
[
log
p (o1:T, s1:T |π)
q (s1:T |π) ]

33. Active inference
!
! active inference AIF
t Gt
q(st |ot, π) ≈ p(st |ot, π)
33
Gt(π) = − 𝔼q(ot, st ∣ π)
[
log
p (ot, st ∣ π)
q (st ∣ π) ]
≈ − 𝔼q(ot, st ∣ π)
[
log
p (ot |π) q (st ∣ ot, π)
q (st ∣ π) ]
= − 𝔼q(ot, st ∣ π) [log p (ot ∣ π)] − 𝔼q(ot ∣ π) [
DKL [q (st ∣ ot, π)||q (st ∣ π)]]

34. Active inference
!
! 1
!
! active inference
!
! 1 0
q = p
34
Gt(π) = − 𝔼q(ot, st ∣ π) [log p (ot ∣ π)] − 𝔼q(ot ∣ π) [
DKL [q (st ∣ ot, π)||q (st ∣ π)]]
= − 𝔼p(ot, st ∣ π) [log p (ot ∣ π)] − 𝔼p(ot ∣ π) [
DKL [p (st ∣ ot, π)||p (st ∣ π)]]
= 𝔼p(st ∣ π) [
ℋ (p (ot ∣ π))]
− I(π) ※ p(st |st−1, π) p(st |π)

35. Active inference
!
! 1
!
! extrinsic value
! 2
! bayesian surprise
! intrinsic value
=>
35
−Gt(π) = 𝔼q(ot,st|π) [log p(ot |π)] + 𝔼q(ot|π) [DKL[q(st |ot, π)||q(st |π)]]

36. Active inference
!
!
!
!
!
[Gershman+ 19]
!
36
˜p(o1:T) = exp(r(o1:T))
※ ˜p

37. Control as inference active inference
37

38. active inference
! Active inference AIF [Millidge+ 20]
!
!
! t −Gt(ϕ)
38
˜p (st, ot, at) = p(st |ot, at)p(at |st)˜p(ot |at) ≈ q(st |ot, at)p(at |st)˜p(ot |at)
qϕ(st, at) = qϕ (at ∣ st) q(st)
−Gt(ϕ) = 𝔼qϕ(ot, st, at)
[
log
˜p (st, ot, at)
qϕ (st, at) ]
≈ 𝔼qϕ(ot, st, at) [log ˜p (ot |at) + log p (at |st) + log q(st |ot, at) − log qϕ (at |st) − log q(st)]
= 𝔼qϕ(ot, st, at) [log ˜p (ot |at)] − 𝔼qϕ(ot, st, at)
[log qϕ (at |st) − log p(at |st)] + 𝔼qϕ(ot, st, at) [log q(st |ot, at) − log q(st)]
≈ 𝔼q(ot ∣ at) [log ˜p (ot ∣ at)] − 𝔼q(st) [
DKL (qϕ (at ∣ st) ∥p (at ∣ st))]
+ 𝔼q(ot, at ∣ st) [
DKL (q (st ∣ ot, at) ∥q (st ∣ at))]
= 𝔼q(ot ∣ at) [log ˜p (ot ∣ at)] + 𝔼q(st) [
ℋ (qϕ (at ∣ st))]
+ 𝔼q(ot, at ∣ st) [
DKL (q (st ∣ ot, at) ∥q (st ∣ at))]
p (at ∣ st) =
1
| 𝒜|

39. AIF CAI
! CAI
! AIF
! 1
! 2
! AIF
! AIF 3
! CAI AIF
!
39
𝔼q(st,at) [log p ( 𝒪t |st, at)] + 𝔼q(st) [
ℋ (qϕ(at |st))]
𝔼q(ot ∣ at) [log ˜p (ot ∣ at)] + 𝔼q(st) [
ℋ (qϕ (at ∣ st))]
+ 𝔼q(ot, at ∣ st) [
DKL (q (st ∣ ot, at) ∥q (st ∣ at))]

40. Likelihood-AIF
! AIF CAI Likelihood-AIF
!
! CAI
˜p(ot) ˜p(ot |st)
−Gt
q(st) = p(st) p (at ∣ st) =
1
| 𝒜|
40
−Gt(ϕ) = 𝔼qϕ(ot, st, at)
[
log
˜p (st, ot, at)
qϕ (st, at) ]
= 𝔼qϕ(ot, st, at) [log ˜p (ot ∣ st) + log p (st) + log p (at ∣ st) − log qϕ (at ∣ st) − log q (st)]
= 𝔼qϕ(st, at) [log ˜p (ot ∣ st)] − DKL (q (st)||p (st)) − 𝔼q(st) [
DKL (qϕ (at ∣ st)||p (at ∣ st))]
−Gt(ϕ) = 𝔼qϕ(st, at) [log ˜p (ot |st)] + 𝔼q(st) [
ℋ (qϕ (at ∣ st))]

41. Likelihood-AIF CAI
! CAI
! Likelihood-AIF
! 2
! AIF POMDP MDP CAI 1
! CAI
! 2
log ˜p (ot ∣ st) = log p ( 𝒪t |st, at)
41
𝔼qϕ(st,at) [log p ( 𝒪t |st, at)] + 𝔼q(st) [
ℋ (qϕ(at |st))]
𝔼qϕ(st, at) [log ˜p (ot |st)] + 𝔼q(st) [
ℋ (qϕ (at ∣ st))]

42. CAI AIF
! CAI
!
!
!
!
! AIF
!
!
!
42

43. !
1.
! Control as inference
! Amortized
! Variational RL
2.
! active inference
!
!
!
43