PRML, sec6 slide.

1. PRML §6 — kernel method
@taki0313
10/10/22
@taki0313

2. 1/50
ToC
Introduction
6.1 双対表現
6.2 カーネル関数の構成
6.3 RBFネットワーク
6.4 ガウス過程
@taki0313

3. 2/50
Introduction
@§3 回帰 / @§4 分類 — linear, parametric
kernel function k(x, x′
) = φ(x)T
φ(x′
)
– ある特徴空間上での内積, 対称k(x, x′
) = k(x′
, x)
– 恒等カーネル k(x, x′
) = xT
x′
– 不変カーネル k(x, x′
) = k(x − x′
)
– 均一カーネル k(x, x′
) = k(||x − x′
||)
kernel trick
– kernelを用いて特徴空間上でごにょごにょする技法
@taki0313

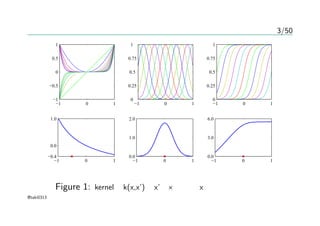
4. 3/50
−1 0 1
−1
−0.5
0
0.5
1
−1 0 1
0
0.25
0.5
0.75
1
−1 0 1
0
0.25
0.5
0.75
1
−1 0 1
−0.4
0.0
1.0
−1 0 1
0.0
1.0
2.0
−1 0 1
0.0
3.0
6.0
Figure 1: kernelとk(x,x’)をx’を×としてxの関数にしたもの
@taki0313

5. 4/50
ToC
Introduction
6.1 双対表現
6.2 カーネル関数の構成
6.3 RBFネットワーク
6.4 ガウス過程
@taki0313

6. 5/50
双対表現 — dual representation
正則化項付き線形回帰の評価式
– J(w) = 1
2
∑
{wT
φ(xn) − tn}2
+ λ
2 wT
w
– wについての勾配=0
w = −1
λ
∑
{wT
φ(xn)}φ(xn) =
∑
anφ(xn) = ΦT
a
– ΦT
= (φ(x1) · · · φ(xN))
パラメータの変換 w a — w = ΦT
a → J(w)
– J(a) = 1
2aT
ΦΦT
ΦΦT
a − aT
ΦΦT
t + 1
2tT
t + λ
2 aT
ΦΦT
a
グラム行列 — Knm ≡ φ(xn)T
φ(xm) = k(xn, xm)
@taki0313

7. 6/50
双対表現 — dual representation
Kを用いて
– K = ΦΦT
– J(a) = 1
2aT
KKa − aT
Kt + 1
2tT
t + λ
2 aT
Ka
w = ΦT
a を an の式に代入して
– λan + aT
Φφ(xn) = tn → (λIN + K)a = t
予測の式
– y(x) = aT
Φφ(x)
– y(x) = k(x)
T
(K + λIN)−1
t — k(x) = k(xn, x)
@taki0313

8. 7/50
双対表現 — dual representation
kernel method — グラム行列K(NxN)の逆行列を求める
基底関数 — 計画行列Φ(MxM)の逆行列を求める
一般に…
– N >> M
– グラム行列の逆行列を求めるコストは大きい 全てをカーネ
ルk の上で行なえるのが嬉しいことらしい。
@taki0313

9. 8/50
ToC
Introduction
6.1 双対表現
6.2 カーネル関数の構成
6.3 RBFネットワーク
6.4 ガウス過程
@taki0313

10. 9/50
カーネル関数の構成
カーネル関数 — 特徴空間上への写像 φ(x)
カーネルkが有効か? ある空間上での内積になること
– (xT
z)2
= (x1z1 + x2z2)2
= x2
1 z2
1 + 2x1z1x2z2 + x2
2 z2
2
– = (x2
1 ,
√
2x1x2, x2
2 )(z2
1 ,
√
2z1z2, z2
2 )T
= φ (x)
T
φ (z)
カーネルkが有効か? グラム行列K が半正定値行列
カーネルの構成法 — (6.13) ∼ (6.22)
@taki0313

11. 10/50
カーネルの作り方
k(x, x′
) = ck1(x, x′
)
k(x, x′
) = f (x)k1(x, x′
)f (x′
)
k(x, x′
) = q(k1(x, x′
))
k(x, x′
) = exp(k1(x, x′
))
k(x, x′
) = k1(x, x′
) + k2(x, x′
)
k(x, x′
) = k1(x, x′
)k2(x, x′
)
k(x, x′
) = k3(φ(x), φ(x′
))
k(x, x′
) = xT
Ax
k(x, x′
) = ka(xa, x′
a) + kb(xb, x′
b)
k(x, x′
) = ka(xa, x′
a)kb(xb, x′
b)
– cは定数、fは任意の
関数
– qは非負の係数をも
つ多項式
– Φ : x → RM
– k3はRM
上のkernel
– Aは対称, 半正定値
– x = (xa, xb)
– ka, kb はそれぞれで
有効なkernel
@taki0313

12. 11/50
有名なカーネル
ガウスカーネル k(x, x′
) = exp(−1
2||x − x′
||2
)
– ||x − x′
||2
= xT
x + (x′
)T
x′
− 2xT
x′
– カーネルトリック — → κ(x, x) + κ(x′
, x′
) − 2κ(x, x′
)
シグモイドカーネル k(x, x′
) = tanh(axT
x′
+ b)
@taki0313

13. 12/50
確率的生成モデル → カーネル
生成モデル p(x) → k(x, x′
) = p(x)p(x′
)
一般化
– 離散 — k(x, x′
) =
∑
i p(x|i)p(x′
|i)p(i)
– 連続 — k(x, x′
) =
∫
p(x|z)p(x′
|z)p(z)dz
HMM → §13
– よく知らないので…
– k(X, X′
) =
∑
Z p(X|Z)p(X′
|Z)p(Z)
@taki0313

14. 13/50
生成モデル → カーネル
parametric な生成モデル — p(x|θ)
フィッシャーカーネル
– フィッシャースコア — g(θ, x) = ∇θ ln p(x|θ)
– フィッシャー情報量行列 — F = Eθ[g(θ, x)g(θ, x)T
]
近似 — F ∼ 1
N
∑
g(θ, xn)g(θ, xn)T
– フィッシャーカーネル
∗ k(x, x′
) = g(θ, x)T
F−1
g(θ, x′
)
∗ k(x, x′
) = g(θ, x)T
g(θ, x′
)
@taki0313

15. 14/50
ToC
Introduction
6.1 双対表現
6.2 カーネル関数の構成
6.3 RBFネットワーク
6.4 ガウス過程
@taki0313

16. 15/50
RBF network — Radial Basis Function
関数補間
– 入力集合 {x1, x2, · · · , xN, }{t1, t2, · · · , tN}
– 1 ≤ n ≤ N について f (xn) = tn になる関数fを求める
– f (x) =
∑
wnh(||x − xn||) として{wn} を最小二乗法で求める。
— 過学習
ノイズが入る場合の補間
– ノイズの分布 ν(ξ) — 確率変数ξ
– 二乗誤差 E = 1
2
∑N
n=1
∫
{y(xn + ξ) − tn}2
ν(ξ)dξ
@taki0313

17. 16/50
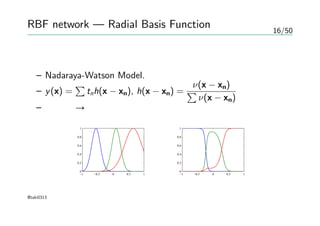
RBF network — Radial Basis Function
変分法による最適化
– Nadaraya-Watson Model.
– y(x) =
∑
tnh(x − xn), h(x − xn) =
ν(x − xn)
∑
ν(x − xn)
– 正則化 → 全ての関数が小さい値にならにように
−1 −0.5 0 0.5 1
0
0.2
0.4
0.6
0.8
1
−1 −0.5 0 0.5 1
0
0.2
0.4
0.6
0.8
1
@taki0313

18. 17/50
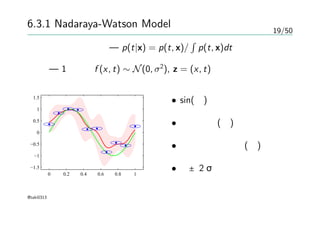
6.3.1 Nadaraya-Watson Model
§3.3.3 — 新しい入力xに対する予測を線形結合の式で行う
– y(x, mN) =
∑
k(x, xn)tn — 等価カーネル
– 和の制約を満たしている
回帰 密度推定
– 訓練集合 {xn, tn} → p(x, t)の推定 — Parzen推定法(§2.5.1)
– p(x, t) = 1
N
∑
f (x − xn, t − tn) — 各要素を中心に持つ
– 条件付き期待値 が良い — y(x) = E[t|x] =
∫ ∞
−∞
tp(t|x)dt
– E[t|x] =
∫
tpdt
∫
pdt
=
∑
n
∫
tf (x − xn, t − tn)dt
∑
m
∫
f (x − xm, t − tm)dt
@taki0313

19. 18/50
6.3.1 Nadaraya-Watson Model
y(x) = E[t|x] =
∫
tpdt
∫
pdt
=
∑
n
∫
tf (x − xn, t − tn)dt
∑
m
∫
f (x − xm, t − tm)dt
簡単化 — 各要素の平均は0 —
∫
tf (x, t)dt = 0
変数置換 → Nadaraya-Watson Model
– y(x) =
∑
n g(x − xn)tn/
∑
m g(x − xm) =
∑
n k(x, xn)tn
– g(x) =
∫ ∞
−∞
f (x, t)dt
– k(x, xn) = g(x − xn)/
∑
m g(x − xm)
@taki0313

20. 19/50
6.3.1 Nadaraya-Watson Model
条件付き確率分布— p(t|x) = p(t, x)/
∫
p(t, x)dt
例 — 1次元、f (x, t) ∼ N(0, σ2
), z = (x, t) の場合
0 0.2 0.4 0.6 0.8 1
−1.5
−1
−0.5
0
0.5
1
1.5
• sin(緑)
• データ点(青)
• 条件付き期待値(赤)
• 赤±2σ
@taki0313

21. 20/50
ToC
Introduction
6.1 双対表現
6.2 カーネル関数の構成
6.3 RBFネットワーク
6.4 ガウス過程
@taki0313

22. 21/50
ガウス過程
確率過程
– 任意の有限な値集合 {y1, y2, · · · , yn}に対して矛盾のない同時
分布を与えるもの
– その同時分布がガウス分布 — ガウス過程
§6.1 回帰、双対性→カーネル — 非確率的モデル
確率的識別モデル + カーネル法 — ガウス過程
@taki0313

23. 22/50
6.4.1 線形回帰の復習
線形回帰モデルy(x) = wT
φ(x)
パラメータの事前分布 p(w) = N(w|0, α−1
I)
入力 {x1, x2, · · · , xN}による評価
{y(x1), y(x2), · · · , y(xN)}による評価
→ {yn}, y = (y1, y2, · · · , yN)T
を評価する
– E[y] = ΦE[w] = 0
– Cov[y] = ΦCov[wwT
]ΦT
= 1
αΦΦT
= K
– Knm = k(xn, xm) = 1
α φ(xn)T
φ(xm)
線形回帰はガウス過程の特殊な場合
@taki0313

24. 23/50
ガウス過程
同時分布の性質が平均、共分散で完全に記述される
– 平均(1次モーメント) =0とする = p(w|α)の平均を0
– ガウス過程 ← カーネル関数 — E[y(xn), y(xm)] = k(xn, xm)
−1 −0.5 0 0.5 1
−3
−1.5
0
1.5
3
−1 −0.5 0 0.5 1
−3
−1.5
0
1.5
3
カーネル&ガウス過程から取り出した関数
@taki0313

25. 24/50
カーネル関数の直接定義
図(左) — ガウスカーネル k(x, x′
) = exp(−||x−x′
||2
2σ2 )
図(右) — 指数カーネル k(x, x) = exp(−θ|x − x′
|)
— オルンシュタイン-ウーレンベック過程
@taki0313

26. 25/50
6.4.2 ガウス過程による回帰
ガウス分布のノイズを考える — tn = yn + εn
p(tn|yn) = N(tn|yn, β−1
)
データ y = (y1, · · · , yN)T
と t = (t1, · · · , tN)が与えられる
その同時分布が等方的ガウス分布になるとする(ガウス過程)
– p(t|y) = N(t|y, β−1
IN)
– p(y) = N(y|0, K)
– K は xn, xm が似ていれば大きい値になる
実際の予測のための分布 p(t)
@taki0313

27. 26/50
6.4.2 ガウス過程による回帰
実際の予測のための分布 p(t)を考える
– p(t) =
∫
p(t|y)p(y)dy ∼ N(t|0, C)
– C(xn, xm) = k(xn, xm) + β−1
δnm
– データとノイズが独立なので共分散を加えるだけでいい
回帰に使われるようなモデル
k(xn, xm) = θ0 exp{−θ1
2 ||xn − xm||2
} + θ2 + θ3xT
n xm
— (θ0, θ1, θ2, θ3)毎のプロット : 図6.5
@taki0313

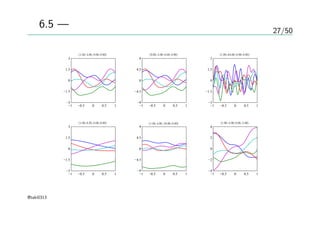
28. 27/50
図6.5 — 事前分布からのサンプル
(1.00, 4.00, 0.00, 0.00)
−1 −0.5 0 0.5 1
−3
−1.5
0
1.5
3
(9.00, 4.00, 0.00, 0.00)
−1 −0.5 0 0.5 1
−9
−4.5
0
4.5
9
(1.00, 64.00, 0.00, 0.00)
−1 −0.5 0 0.5 1
−3
−1.5
0
1.5
3
(1.00, 0.25, 0.00, 0.00)
−1 −0.5 0 0.5 1
−3
−1.5
0
1.5
3
(1.00, 4.00, 10.00, 0.00)
−1 −0.5 0 0.5 1
−9
−4.5
0
4.5
9
(1.00, 4.00, 0.00, 5.00)
−1 −0.5 0 0.5 1
−4
−2
0
2
4
@taki0313

29. 28/50
図6.6 — 同時分布からのサンプル
x
t
−1 0 1
−3
0
3
ガウス過程の事前分布から
サンプリングされた関数f
入力 {xn}
入力に対する{yn} (赤)
サンプル {tn}(緑)
– ノイズ入り
@taki0313

30. 29/50
6.4.2 ガウス過程による回帰
これまで — ガウス過程の視点からの同時分布のモデル化
新しい入力に対する予測が必要
– 訓練集合 {x1, · · · , xN}, t = (t1, · · · , tN)T
– 入力 xN+1 , その予測値 tN+1
– 予測分布 p(tN+1|tN)
– 同時分布 p(tN) を書き下す
– tN+1 = (t1, · · · , tN, tN+1)T
@taki0313

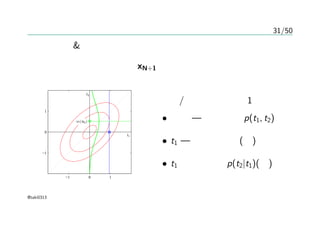
31. 30/50
予測分布
p(tN+1) = N(tN+1|0, CN+1) — (6.61)より
共分散行列の分割
— CN+1 =
(
CN k
kT
c
)
— 正定値でなければならない
— c = k(xN+1, xN+1) + β−1
, kの要素はk(xn, xN+1)
2章の結果から、条件付き分布p(tN+1|t)は
– m(xN+1) = kT
C−1
N t
– σ2
(xN+1) = c − kT
C−1
N k
@taki0313

32. 31/50
予測分布
事前分布&条件付き分布はガウス分布
予測分布の平均・分散もxN+1 に依存
t1
t2
m(x2)
−1 0 1
−1
0
1
訓練/テストデータが1つずつ
• 楕円 — 同時分布 p(t1, t2)
• t1 — 訓練データ(青)
• t1 に依存して p(t2|t1)(緑)
@taki0313

33. 32/50
予測分布
ガウス過程による回帰の例
0 0.2 0.4 0.6 0.8 1
−1
−0.5
0
0.5
1
• sin関数(緑)
• データ(右3つ以外, 青)
• ガウス過程による予測分布
の平均(赤)
• 標準分布の2倍ぐらい(薄い
赤)
@taki0313

34. 33/50
6.4.2 ガウス過程による回帰
Kの固有値λi → Cの固有値λi + β−1
– k(xn, xm)が∀xn, xm に関して半正定値であればいい
予測分布の平均
– m(xN+1) =
∑
ank(xn, xN+1)
– an はC−1
N tのn番目の要素
– kが動径に依存するならRBFが使える
計算量
– ガウス過程 NxNの逆行列 O(N3
) — 基底による回帰 O(M3
)
@taki0313

35. 34/50
6.4.3 超パラメータの学習
予測が共分散の選び方にある程度依存する → parametric
ハイパーパラメータθ → p(t|θ)
– θの点推定, 共役勾配法
ガウス分布&ガウス過程では…
– ln p(t|θ) = −1
2 ln |CN| − 1
2tT
C−1
N t − N
2 ln(2π)
– 勾配 — ∂
∂θi
ln p(t|θ) = −1
2Tr(C−1
N
∂CN
∂θi
) + 1
2tT
C−1
N
∂CN
∂θi
C−1
N t
一般には非凸関数で、近似的に解く。以下略
@taki0313

36. 35/50
6.4.4 関連度自動決定
関連度自由決定(ARD) — ニューラルネットから提案された何か
詳しくは §7.2.2
例 — 2次元の入力空間x = (x1, x2)をもつガウス過程
– カーネル k(x, x′
) = θ0 exp
{
−1
2
∑
ηi(xi − x′
i )2
}
@taki0313

37. 36/50
図6.9 — ARD事前分布からのサンプル
−1
0
1
−1
0
1
−1
0
1
−1
0
1
−1
0
1
−1
0
1
η1 = η2 = 1 (左)
η1 = 1, η2 = 0.01 (右)
ηは入力に対する敏感さ
ARDの文脈から出力の予測
にあまり寄与しない入力変
数を求められる。
@taki0313

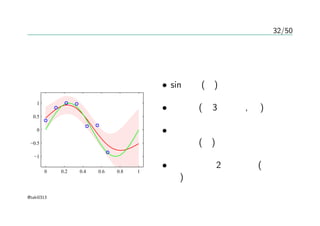
38. 37/50
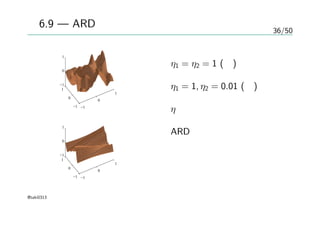
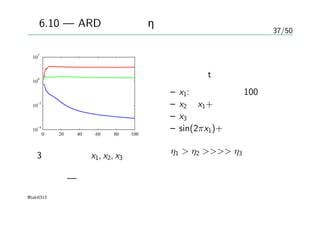
図6.10 — ARDにおけるηの変化
0 20 40 60 80 100
10
−4
10
−2
10
0
10
2
3次元の入力 x1, x2, x3
最適化 — 共役勾配法
目標変数t
– x1:ガウス分布、100個
– x2 はx1+ノイズ
– x3 はランダムなノイズ
– sin(2πx1)+ノイズ
η1 > η2 >>>> η3
@taki0313

39. 38/50
6.4.4 ARD
ARD → 指数・2次カーネル
– k(xn, xm) = θ0 exp{−1
2
∑
ηi(xni − xmi)2
} + θ2 + θ3
∑
xnixmi
種々の応用において有用らしいカーネル
@taki0313

40. 39/50
6.4.5 ガウス過程による分類
確率的な分類 → 事後確率 ∈ (0, 1)
ガウス過程 → 実数値全体 → 活性化関数 → 分類問題
2クラス分類問題 t ∈ {0, 1}
– 関数a(x)上でのガウス過程を考える
– y = σ(a)と変換する
– y ∈ {0, 1}へ落とす
– 1次元の例 — 図6.11
@taki0313

41. 40/50
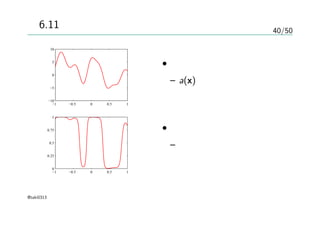
図6.11
−1 −0.5 0 0.5 1
−10
−5
0
5
10
−1 −0.5 0 0.5 1
0
0.25
0.5
0.75
1
• 上図
– a(x)に対するガウス過程
の事前分布からのサンプ
ル
• 下図
– ロジスティックシグモイ
ド関数で変換した
@taki0313

42. 41/50
6.4.5 ガウス過程による分類
目標変数tの確率分布 — ベルヌーイ分布
– p(t|a) = σ(a)t
(1 − σ(a))1−t
入力の訓練集合{x1, · · · , xN}
対応する目標変数の観測値t = (t1, t2 · · · , tN)T
テスト点xN+1 に対するtN+1 を予測
– 予測分布p(tN+1|t)を決定する
– 要素a(x1), · · · , a(xN+1)を持つベクトルaN+1
@taki0313

43. 42/50
6.4.5 ガウス過程による分類
ベクトルaN+1 い対するガウス過程による事前分布
– p(aN+1) = N(aN+1|0, CN+1)
– 正しいラベルが付いている → CN にはノイズが入ってない
– 正定値保証のためにパラメータν の項を入れる
– C(xn, xm) = k(xn, xm) + νδnm
– カーネルはパラメータθによって決まる
2クラス分類 — p(tN+1 = 1|tN)を予測する
– p(tN+1 = 1|tN) =
∫
p(tN+1 = 1|aN+1)p(aN+1|tN)daN+1
@taki0313

44. 43/50
6.4.5 ガウス過程による分類
p(tN+1 = 1|tN) =
∫
p(tN+1 = 1|aN+1)p(aN+1|tN)daN+1
解析的に解けない
– 詳細略
– 漸近的にガウス分布に近づく
– どうやってガウス分布として近似するか
∗ 10.1 変分推論法
∗ 10.7 EP法
∗ 6.4.6 ラプラス近似
@taki0313

45. 44/50
6.4.6 ラプラス近似
ベイズの定理 & p(tN|aN+1, aN) = p(tN|aN) より
p(aN+1|tN) =
∫
p(aN+1, aN|tN)daN
=
1
p(tN)
∫
p(aN+1, aN)p(tN|aN+1, aN)daN
=
1
p(tN)
∫
p(aN+1|aN)p(aN)p(tN|aN)daN
=
∫
p(aN+1|aN)p(aN|tN)daN
@taki0313

46. 45/50
6.4.6 ラプラス近似
条件付き分布 — (6.66), (6.67)
– p(aN+1|aN) = N(aN+1|kT
C−1
N aN, c − kT
C−1
N k)
積分 → ラプラス近似 & ガウス分布の畳み込み
p(aN) — 平均0, 共分散行列CN であるガウス過程による
データについての項(各々独立として…)
– p(tN|aN) =
∏N
n=1 σ(an)tn(1 − σ(an))1−tn =
∏N
n=1 eantnσ(−an)
@taki0313

47. 46/50
6.4.6 ラプラス近似
定数項を無視してラプラス近似
– Ψ(aN) = ln p(aN) + ln p(tN|aN)
= −1
2aT
NCNaN − N
2 ln(2π) − 1
2 ln |CN| + tT
NaN −
∑N
n=1 ln(1 + ean)
– ∇Ψ(aN) = tN − σN − C−1
N aN
σN の要素はσ(an)
– ∇∇Ψ(aN) = −WN − C−1
N
Wは対角要素にσ(an)(1 − σ(an))を持つ正定値行列
dσ
da = σ(1 − σ)(4.88)
正定値行列の和も正定値行列 (演習6.24)
@taki0313

48. 47/50
6.4.6 ラプラス近似
ヘッセ行列 A = −∇∇Ψ(aN)が正定値 — 事後分布p(aN|tN)の対
数が凸関数
凸関数 — 極小・極大 = 最小・最大
逐次更新で最適解を目指せる — Newton-Raphson medhot (4.92)
– anew
N = CN(I + WNCN)−1
{tN−σN + WnaN}
– a∗
N に収束するまで — モード
– このとき a∗
N = CN(tN−σN)
収束時のヘッセ行列 H = −∇∇Ψ(aN) = WN + C−1
N
@taki0313

49. 48/50
6.4.6 ラプラス近似
収束時の、事後分布p(aN|tN)のガウス分布による近似
– q(aN) = N(aN|a∗
N, H−1
)
2つのガウス分布の畳み込み積分の評価 — 2章
– E[aN+1|tN] = kT
(tN − σN)
– var[aN+1|tN] = c − kT
(W−1
N + CN)−1
k
→ガウス分布の情報が得られたので…
@taki0313

50. 49/50
6.4.6 ラプラス近似
共分散パラメータθの決定
– 尤度最大化, 最尤推定
– 尤度関数p(tN|θ) =
∫
p(tN|aN)p(aN|θ)daN
近似
– ln p(tN|θ) = Ψ(a∗
N) − 1
2 ln |WN + C−1
N | + N
2 ln(2π)
Ψ(a∗
N) = ln p(a∗
N) + ln p(tN|a∗
N)
θの微分がCN とaN の二種類の項が表れる(以下略?)
@taki0313

51. 50/50
6.4.7 ニューラルネットとの関係
ニューラルネット
– 隠れユニットの数Mを上手く調整すれば強い
– M → ∞ ガウス過程っぽい. ただし独立
– ニューラルネット — 隠れユニットの共有とが面白い
ガウス過程
– 共分散関数に性質が左右される
– 解析的に求められないところは近似
@taki0313