More Related Content
PDF
PPTX
深層学習の数理:カーネル法, スパース推定との接点 PDF
PPTX
[DL輪読会]GQNと関連研究,世界モデルとの関係について PDF
PDF
PDF
PPTX
What's hot
PDF
スパースモデリング、スパースコーディングとその数理(第11回WBA若手の会) PDF
PDF
PDF
PDF
PPTX
PDF
SSII2022 [SS2] 少ないデータやラベルを効率的に活用する機械学習技術 〜 足りない情報をどのように補うか?〜 PDF
ゼロから始める深層強化学習(NLP2018講演資料)/ Introduction of Deep Reinforcement Learning PDF
PDF
PPTX
PDF
SSII2021 [TS2] 深層強化学習 〜 強化学習の基礎から応用まで 〜 PDF
PDF
[DL輪読会]Progressive Growing of GANs for Improved Quality, Stability, and Varia... PDF
PPTX
Swin Transformer (ICCV'21 Best Paper) を完璧に理解する資料 PPTX
PDF
PPTX
ベイズ深層学習5章 ニューラルネットワークのベイズ推論 Bayesian deep learning PDF
NIPS KANSAI Reading Group #7: 逆強化学習の行動解析への応用 Viewers also liked
PDF
統計的学習理論チュートリアル: 基礎から応用まで (Ibis2012) PDF
PDF
PPT
PPTX
Oracle property and_hdm_pkg_rigorouslasso PDF
PDF
PDF
PDF
Stochastic Alternating Direction Method of Multipliers PDF
スパース性に基づく機械学習 4.1 ノイズなしL1ノルム最小化問題の問題設定 PPTX
Introduction of "the alternate features search" using R PDF
PDF
Similar to Sparse estimation tutorial 2014
PDF
PDF
行列およびテンソルデータに対する機械学習(数理助教の会 2011/11/28) PDF
PPTX
PDF
PDF
PDF
東京都市大学 データ解析入門 5 スパース性と圧縮センシング 2 PDF
2013.12.26 prml勉強会 線形回帰モデル3.2~3.4 PDF
[PRML] パターン認識と機械学習(第3章:線形回帰モデル) PDF
クラシックな機械学習の入門 4. 学習データと予測性能 PDF
PDF
PDF
2014年5月14日_水曜セミナー発表内容_FINAL PDF
PPTX
PPTX
スパース性に基づく機械学習(機械学習プロフェッショナルシリーズ) 3.3節と3.4節 PDF
ML: Sparse regression CH.13 PDF
PATTERN RECOGNITION AND MACHINE LEARNING (1.1) PDF
PDF
More from Taiji Suzuki
PPTX
PDF
PDF
PDF
PPTX
[ICLR2021 (spotlight)] Benefit of deep learning with non-convex noisy gradien... PDF
Minimax optimal alternating minimization \\ for kernel nonparametric tensor l... PDF
PAC-Bayesian Bound for Gaussian Process Regression and Multiple Kernel Additi... PDF
[NeurIPS2020 (spotlight)] Generalization bound of globally optimal non convex... PPTX
Iclr2020: Compression based bound for non-compressed network: unified general... PDF
Sparse estimation tutorial 2014
- 1.
スパース推定概観:モデル・理論・応用
y 鈴木 大慈
yTokyo Institute of Technology
Department of Mathematical and Computing Sciences
2014 年9 月15 日
統計連合大会@東京大学
1 / 56
- 2.
Outline
1 スパース推定のモデル
2 いろいろなスパース正則化
3 スパース推定の理論
n ≫ p の理論
n ≪ p の理論
4 高次元線形回帰の検定
5 スパース推定の最適化手法
2 / 56
- 3.
高次元データでの問題意識
ゲノムデータ
金融データ
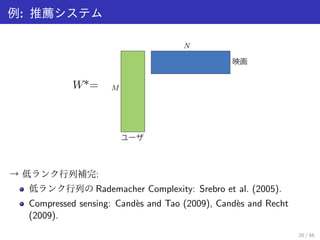
協調フィルタリング
コンピュータビジョン
音声認識
次元d = 10000 の時,サンプル数n = 1000 で推定ができるか?
どのような条件があれば推定が可能か?
何らかの低次元性(スパース性) を利用.
3 / 56
- 4.
歴史: スパース推定の手法と理論
1992Donoho and Johnstone Wavelet shrinkage
(Soft-thresholding)
1996 Tibshirani Lasso の提案
2000 Knight and Fu Lasso の漸近分布
(n ≫ p)
2006 Candes and Tao, 圧縮センシング
Donoho (制限等長性,完全復元,p ≫ n)
2009 Bickel et al., Zhang 制限固有値条件
(Lasso のリスク評価, p ≫ n)
2013 van de Geer et al., スパース推定における検定
Lockhart et al. (p ≫ n)
これ以前にも反射法地震探査や画像雑音除去,忘却付き構造学習にL1 正則化は使われて
いた.詳しくは田中利幸(2010) を参照. 4 / 56
- 5.
Outline
1 スパース推定のモデル
2 いろいろなスパース正則化
3 スパース推定の理論
n ≫ p の理論
n ≪ p の理論
4 高次元線形回帰の検定
5 スパース推定の最適化手法
5 / 56
- 6.
- 7.
- 8.
スパース推定
サンプル数≪ 次元
無駄な情報を切り落とす→スパース性
Lasso 推定量
R. Tsibshirani (1996). Regression shrinkage and selection via the lasso.
J. Royal. Statist. Soc B., Vol. 58, No. 1, pages 267{288.
引用数:10185 (2014 年5 月25 日)
7 / 56
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
j j.
→凸最適化!
L1 ノルムはL0 ノルムの[1; 1]p にお
ける凸包(下から抑える最大の凸関数)
L1 ノルムは要素数関数のLovasz 拡張
9 / 56
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
Lasso;i = argmin
b2R
1
2
(yi b)2 + Cjbj
=
{
sign(yi )(yi C) (jyi j C)
0 (jyi j C):
小さいシグナルは0 に縮小される→スパース!
10 / 56
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
j j:
Theorem(Lasso の収束レート)
ある条件のもと,定数C が存在して高い確率で次の不等式が成り立つ:
∥ ^ - 52.
∥22
C
dlog(p)
n
:
※次元が高くても,たかだかlog(p) でしか効いてこない.実質的な次元
d が支配的.
(「ある条件」については後で詳細を説明)
12 / 56
- 53.
Outline
1 スパース推定のモデル
2 いろいろなスパース正則化
3 スパース推定の理論
n ≫ p の理論
n ≪ p の理論
4 高次元線形回帰の検定
5 スパース推定の最適化手法
13 / 56
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
∥| {z }1
(yi x
正則化項
:
一般化したスパース正則化推定法:
min
w2Rp
1
n
Σn
i=1
ℓ(zi ; - 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
(t) (i =1; : : : ; n(t); t = 1; : : : ;T):
min
- 69.
- 70.
- 71.
- 72.
(T)
k )∥
| {z }
グループ正則化
:
b(1)b(2) b(T)
*URXS
*URXS
؞؞؞؞؞؞
*URXS
タスク間共通で非ゼロな変数を選択
17 / 56
- 73.
- 74.
(t) (i =1; : : : ; n(t); t = 1; : : : ;T):
min
- 75.

















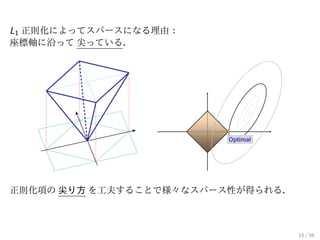








![∥0 は凸関数ではない.連続でもない.沢山の局所最適解.
→ 凸関数で近似.
Lasso [L1 正則化]
^](https://image.slidesharecdn.com/sparsetutorial2014-140916025106-phpapp01/85/Sparse-estimation-tutorial-2014-28-320.jpg)





![j j.
→ 凸最適化!
L1 ノルムはL0 ノルムの[1; 1]p にお
ける凸包(下から抑える最大の凸関数)
L1 ノルムは要素数関数のLovasz 拡張
9 / 56](https://image.slidesharecdn.com/sparsetutorial2014-140916025106-phpapp01/85/Sparse-estimation-tutorial-2014-34-320.jpg)