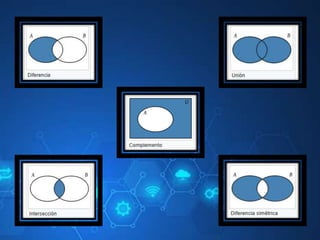
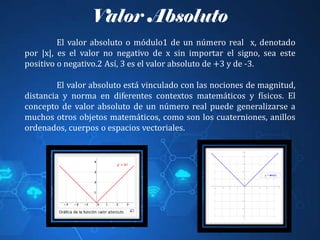
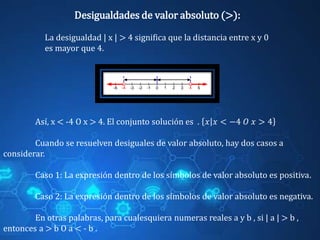
El documento trata sobre conceptos fundamentales de conjuntos y operaciones con ellos, así como de números reales y desigualdades. Se describen operaciones básicas como unión, intersección y diferencia, junto con la notación correspondiente y ejemplos. Además, se abordan desigualdades simples y de valor absoluto, explicando su resolución y representación gráfica.