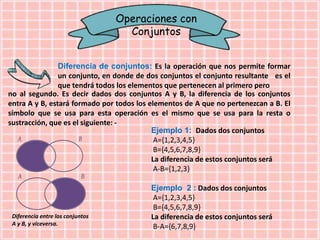
The document discusses sets and real numbers. It defines what a set is and provides examples of set operations like union, intersection, difference and symmetric difference. It then defines real numbers as numbers that have a periodic or non-periodic decimal expansion. Real numbers include rational numbers like integers and fractions as well as irrational numbers. Properties of real numbers like commutativity, associativity and distributivity are stated. Inequalities and absolute value are also explained.

1. Números Reales
María Gabriela Díaz Medina
CI: 28020149
República Bolivariana de Venezuela
Ministerio del Poder Popular para la educación
Universidad Politécnica Territorial Andrés Eloy Blanco
Barquisimeto- Edo. Lara

2. ¿Qué es un Conjunto?
En matemáticas, un conjunto lo forman unos elementos de la
misma naturaleza, es decir, elementos diferenciados entre sí
pero que poseen en común ciertas propiedades o
características, y que pueden tener entre ellos, o con los
elementos de otros conjuntos, ciertas relaciones.
Un conjunto puede tener un número finito o infinito
de elementos, en matemáticas normalmente le
utilizan letras mayúsculas A, B, C , X, Y… para denotar
conjuntos.
Y para denotar los elementos se utilizan letras
minúsculas a, b, c… o también números, símbolos y
variables.

3. Operaciones con
Conjuntos
Las operaciones con conjuntos también conocidas como álgebra de conjuntos,
nos permiten realizar operaciones sobre los conjuntos para obtener otro
conjunto. Las operaciones con conjuntos son las siguientes:
Unión o reunión de conjuntos: Es la operación que nos permite
unir dos o más conjuntos para formar otro conjunto que contendrá a
todos los elementos que queremos unir pero sin que se
repitan. Es decir dado un conjunto A y un conjunto B, la unión de los conjuntos A y
B será otro conjunto formado por todos los elementos de A, con todos los
elementos de B sin repetir ningún elemento. El símbolo que se usa para indicar la
operación de unión es el siguiente: ∪.
Ejemplo : Dados dos conjuntos
A={1,2,3,4,5,6}
B={8,9,10,11}
La unión de estos conjuntos será
A∪B={1,2,3,4,5,6,8,9,10,11}
La unión de los
conjuntos A y B es
otro conjunto A ∪ B
que contiene todos
los elementos de A
y B.

4. Operaciones con
Conjuntos
Diferencia de conjuntos: Es la operación que nos permite formar
un conjunto, en donde de dos conjuntos el conjunto resultante es el
que tendrá todos los elementos que pertenecen al primero pero
Ejemplo 1: Dados dos conjuntos
A={1,2,3,4,5}
B={4,5,6,7,8,9}
La diferencia de estos conjuntos será
A-B={1,2,3}
Ejemplo 2 : Dados dos conjuntos
A={1,2,3,4,5}
B={4,5,6,7,8,9}
La diferencia de estos conjuntos será
B-A={6,7,8,9}
no al segundo. Es decir dados dos conjuntos A y B, la diferencia de los conjuntos
entra A y B, estará formado por todos los elementos de A que no pertenezcan a B. El
símbolo que se usa para esta operación es el mismo que se usa para la resta o
sustracción, que es el siguiente: -
Diferencia entre los conjuntos
A y B, y viceversa.

5. Operaciones con
Conjuntos
Intersección de conjuntos: Es la operación que nos permite
formar un conjunto, sólo con los elementos comunes involucrados en
la operación. Es decir dados dos conjuntos A y B, la de
intersección de los conjuntos A y B, estará formado por los elementos de A y los
elementos de B que sean comunes, los elementos no comunes A y B, será excluidos.
El símbolo que se usa para indicar la operación de intersección es el siguiente: ∩.
Ejemplo 1: Dados dos conjuntos
A={1,2,3,4,5}
B={4,5,6,7,8,9}
La intersección de estos conjuntos será
A∩B={4,5}
La intersección de A y B es otro conjunto A ∩ B que contiene sólo los
elementos que pertenecen tanto a A como a B.

6. Operaciones con
Conjuntos
Diferencia simétrica de conjuntos: Es la operación que nos permite
formar un conjunto, en donde de dos conjuntos el conjunto resultante es
el que tendrá todos los elementos que no sean comunes a ambos
conjuntos. Es decir dados dos conjuntos A y B, la diferencia simétrica
estará formado por todos los elementos no comunes a los conjuntos A y
B. El símbolo que se usa para indicar la operación de diferencia simétrica
es el siguiente: △.
Ejemplo : Dados dos conjuntos
A={1,2,3,4,5}
B={4,5,6,7,8,9}
La diferencia simétrica de estos conjuntos será
A △ B={1,2,3,6,7,8,9}
La diferencia simétrica de A y B es el conjunto que contiene todos los
elementos de A y de B salvo aquellos que pertenecen a ambos.

7. Números Reales
Los números reales son aquellos
números que tienen expansión
decimal periódica o tienen expansión
decimal no periódica. Son cualquier
número que corresponda a un punto
en la recta real y pueden clasificarse
en números naturales, enteros,
racionales e irracionales.
Los números reales son los que
pueden ser expresados por un
número o entero o decimal; esto
quiere decir que abarcan a los
números racionales y los números
irracionales.
Los números reales se representan
mediante la letra:
Propiedades:
Propiedad Conmutativa: El orden al sumar
o multiplicar reales no afecta el resultado.
Por ejemplo: a+b = b+a
9+5 = 5+9
Propiedad Asociativa: Realizar diferentes
asociaciones al sumar o multiplicar reales y
no afecta el resultado.
Por ejemplo: a+(b+c)=(a+b)+c
5+(2+7)=(5+2)+7
Propiedad Distributiva: El factor se
distribuye a cada sumando.
Por ejemplo: a (b + c) = ab + ac
3(x+6) = 3(x) + 3(6)

8. Números Reales
Conjunto de los números Reales: Es a unión de dos tipos de números, a saber;
los números racionales, los números irracionales.
A su vez, los números racionales se clasifican en:
Números Naturales (N): Son
los que usamos para contar.
Ej. 1, 2, 3, 4, 5, 6…
N Números Enteros (Z): son los
números naturales, sus negativos y
el cero. Ej. -3, -2, -1, 0
Z
Números Fraccionarios: son
aquellos números que se pueden
expresar como cociente de dos
números enteros, es decir, son
números de la forma a/b con a, b
enteros y b ≠0.
Números Algebraicos: son aquellos
que provienen de la solución de alguna
ecuación algebraica y se representan por
un número finito de radicales libres o
anidados. Ej. √3
√
a/b
𝝅
Números Trascendentales: Estos provienen de las
llamadas funciones trascendentes: trigonométricas,
logarítmicas y exponenciales. El número π y e son
irracionales trascendentes, puesto que no pueden
expresarse mediante radicales.

9. Desigualdades
Una desigualdad es una relación de orden que se da entre dos valores
cuando estos son distintos. Si los valores en cuestión son elementos
de un conjunto ordenado como los enteros o los reales, entonces
pueden ser comparados.
 La notación a < b significa a es menor que b. 3 < 7
 La notación a > b significa a es mayor que b. 7 > 3
 La notación a ≤ b significa a es menor o igual que b. 3 ≤ 7
 La notación a ≥ b significa a es mayor o igual que b. 7 ≥ 3
 La notación a ≪ b significa a es mucho menor que b. 2 ≪10
 La notación a ≫ b significa a es mucho mayor que b. 10 ≫2

10. Valor absoluto
El valor absoluto de un numero real es valor numérico sin tener en cuenta su
signo, sea este positivo (+) o negativo (-). De este modo, 5 es el valor absoluto de
+5 y de -5. Cabe destacar que el valor absoluto se escribe entre dos barras
verticales paralelas; por lo tanto, la notación correcta es |5|.
Para cualquier numero real X, el valor absoluto de X denota por |X|
se define como:
x, si x ≥ 0
-x, si x < 0
|X|
El valor absoluto de X s siempre un número positivo o cero pero nunca negativo:
cuando X es un número negativo (X < 0) entonces su valor absoluto es
necesariamente positivo | x | = − x > 0

11. Desigualdades con Valor
Absoluto
Una desigualdad de valor absoluto es una desigualdad que tiene un signo de
valor absoluto con una variable dentro. Para resolver una desigualdad con
valor absoluto del lado izquierdo y una constante positiva en el otro miembro,
solo hay que identificar con alguna de las dos formas, aplicar la equivalencia,
resolver las desigualdades de la equivalencia para pasar a determinar el
conjunto solución de la desigualdad en base a la condición de la equivalencia.
Ejemplo :
| x – 7| < 3
Para resolver este ejercicio, se descomponer en una desigualdad compuesta.
x – 7 < 3 Y x – 7 > –3
–3 < x – 7 < 3
Sume 7 en cada expresión.
-3 + 7 < x - 7 + 7 < 3 + 7
4 < x <10