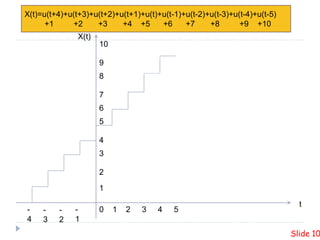
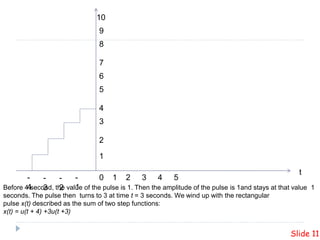
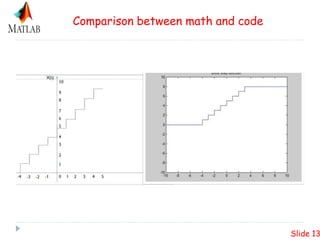
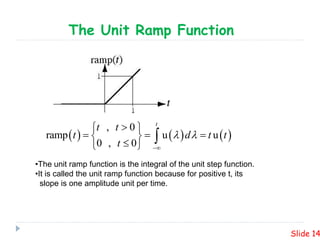
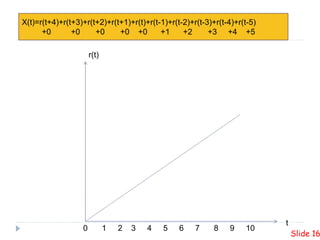
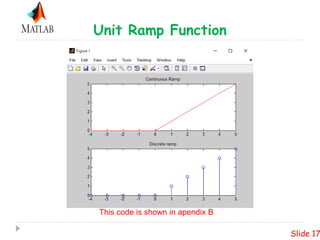
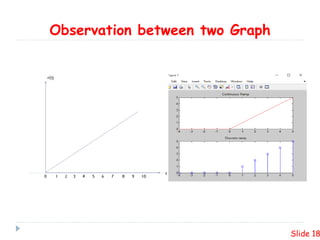
This presentation summarizes plotting unite step and ramp functions in MATLAB. It defines the unit step and ramp functions mathematically and graphically. It shows how to represent the combination of 10 step functions and the corresponding ramp function in MATLAB. Code examples are provided to plot the unit step and ramp functions in MATLAB.

1. PLOTTING UNITE STEP AND RAMP
FUNCTION IN MATLAB
Wellcome to our presentation.
Slide 1

2. Group Members
 MAHMUDULHASAN
Slide 2

3.  Introduction.
 Mathology.
 Plotting function on Matlab
 Define Mathmatically and Graphically
 Conclusion
 Reference
 Apendix
Slide 3
OVERVIEW

4. Idea of the project
 Consider a signal is given.you have to do the following:
 1.the signal is a combination of 10 step function.
 2.The Step functions are defined.
 3.Represent the function graphically.
 4.Find the complete Ramp function.
 5.express mathematically and illustrate graphically.
Slide 4

5. Project description
 We add ten step function randomly in a function.then we find step function
by mathmatically and graphically.we draw in this signal.then we again draw
this signal by using matlab.after that we find ramp fuction from this
equation by mathematically and graphically. then we plot it in mat lab.
Slide 5

6. Perpose of the project
 Know about unite step function.
 Know about ramp function.
 How to plot unite step function in graph.
 How to plot ramp function in graph.
 Matab programme.
Slide 6

7. The Unit Step Function
 Definition: The unit step function, u(t), is defined as
 That is, u is a function of time t, and u has value zero when time is negative (before
we flip the switch); and value one when time is positive (from when we flip the
switch).
Slide 7

8. The Unit Ramp Function
 The ramp function is a unary real function, easily computable as the mean of
the independent variable and its absolute value.
 This function is applied in engineering (e.g., in the theory of DSP). The name ramp
function is derived from the appearance of its graph.
     
, 0
ramp u u
0 , 0
t
t t
t d t t
t
 

 
   
 

Slide 8

9. Draw unite step function
 Draw unite step function graphically
and mathmaticaly
Slide 9

10. -
2
-
4
t
-
3
-
1
0 1 2 3 4 5
1
2
3
4
5
6
7
8
9
10
X(t)
X(t)=u(t+4)+u(t+3)+u(t+2)+u(t+1)+u(t)+u(t-1)+u(t-2)+u(t-3)+u(t-4)+u(t-5)
+1 +2 +3 +4 +5 +6 +7 +8 +9 +10
Slide 10

11. Before 4 second, the value of the pulse is 1. Then the amplitude of the pulse is 1and stays at that value 1
seconds. The pulse then turns to 3 at time t = 3 seconds. We wind up with the rectangular
pulse x(t) described as the sum of two step functions:
x(t) = u(t + 4) +3u(t +3)
-
2
-
4
t
-
3
-
1
0 1 2 3 4 5
1
2
3
4
5
6
7
8
9
10
Slide 11

12. Unit Step Graph matlab
This code is shown in apendix A
Slide 12

13. Comparison between math and code
Slide 13

14. The Unit Ramp Function
     
, 0
ramp u u
0 , 0
t
t t
t d t t
t
 

 
   
 

•The unit ramp function is the integral of the unit step function.
•It is called the unit ramp function because for positive t, its
slope is one amplitude unit per time.
Slide 14

15. Draw unite ramp function
 Draw ramp function graphically and
mathmaticaly
Slide 15

16. t
r(t)
0 1 2 3 4 5 6 7 8 9 10
X(t)=r(t+4)+r(t+3)+r(t+2)+r(t+1)+r(t)+r(t-1)+r(t-2)+r(t-3)+r(t-4)+r(t-5)
+0 +0 +0 +0 +0 +1 +2 +3 +4 +5
Slide 16

17. Unit Ramp Function
This code is shown in apendix B
Slide 17

18. Observation between two Graph
Slide 18

19. Observation:
 The derivative of the ramp function Step function
 The integration of the step function Ramp function
Slide 19

20. Inquiry
2014-2-60-035@ewu.edu.bd
Slide 20

21. Referrance
 https://www.google.com/search?q=unit+st
ep+function+definition&client=firefox-
b&source=lnms&sa=X&ved=0ahUKEwikte
H40JnTAhVMtI8KHU7JB_IQ_AUIBSgA&bi
w=1366&bih=659&dpr=1
 https://www.youtube.com/watch?v=YMve
WtrCOds
https://en.wikipedia.org/wiki/Ramp_function
Slide 21

22. Apendix
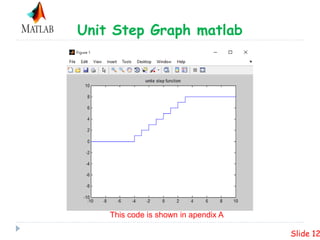
 Matlab code for unite step function
 clear all
 clc
 t=-20:0.001:20;
 y=heaviside(t+4)+heaviside(t+3)+heaviside(t+
2)+heaviside(t+1)+heaviside(t)+heaviside(t-
1)+heaviside(t-2)+heaviside(t-3)
 +heaviside(t-4)+heaviside(t-5);
 plot(t,y);
 axis([-10 10 -10 10])
Slide 22

23. Apendix
 Matlab code for unite Ramp function
 close all;
 clear all;
 clc
 n1=input('Enter lower limit');
 n2=input('Enter upper limit');
 n=n1:n2;
 x=n.*[n>=0];
 subplot(2,1,1);
 plot(n,x,'r');
 title('Continuous');
 subplot(2,1,2);
 stem(n,x,'b');
 title('Discrete');
Slide 23