The document is a practical file from Sri Sai Institute of Engineering and Technology detailing various MATLAB programs for digital signal processing, including functions for impulse, step, ramp, exponential, and real value sequences. It provides an introduction to MATLAB, highlighting its capabilities, key features, and characteristics, as well as practical applications in engineering. Additionally, the file includes code snippets for different signal processing tasks and their corresponding graphical outputs.

1.
SRI SAI INSTITUTE OF ENGG. AND TECHNOLOGY
MATLAB PRACTICAL FILE
DSP
ECE - 316
Submitted By:
Abhishek Sharma
ECE - 6th Sem.

2. TABLE OF CONTENTS
Contents
Inroduction To MATLAB _____________________________________________________________________ 1
Program For Impulse Function _____________________________________________________________ 4
Program For Unit Step Function ____________________________________________________________ 6
Program For Unit Ramp Function __________________________________________________________ 8
Program For Exponential Function ______________________________________________________ 10
Program For Real Value Function ________________________________________________________ 16
Program For Shifting Function ___________________________________________________________ 14
_
Program For Addition Function ___________________________________________________________ 16
Program For Multiplication Function ____________________________________________________ 18
Program For Convolution Function ______________________________________________________ 20
Program For Folding Function ____________________________________________________________ 23

3. WHAT IS MATLAB?
“AN INTRODUCTION”
• It stands for MATrix LAbORATORY
• It is developed by The Mathworks Inc.
• It is an interactive, integrated, environment
• For numerical computations
• For symbolic computations
• For scientific visualizations
• It is a high level programming language
• Program runs in interpreted, as opposed to compiled, mode
• MATLAB is a high level technical computing language and interactive environment for
algorithm development, data visualization, data analysis and numeric computation. Using
the MATLAB product, you can solve technical computing problems faster than the
traditional programming languages such as C, C++ and FORTRAN.
• You can use MATLAB in a wide range of applications, including signal and image processing,
communication, control design, test and measurement, financial modeling and analysis, and
computational biology. Add on toolboxes(collection of special purpose MATLAB functions,
available separately) extend the MATLAB environment to solve particular classes of
problems in these application areas.
• MATLAB provides a number of features for documenting and sharing your work. You can
integrate your MATLAB code with other languages and applications, and distribute your
MATLAB algorithms and applications.
1

4. Characterstics Of MATLAB:
• Programming Language Based(principally) On Matrices.
• Slow compared with FORTRAN or C because it is an interpreted language, i.e not pre‐
compiled. Avoid for loops, instead use vector form whenever possible.
• Automatic memory management, i.e you don’t have to declare arrays in advance.
• Intuitive, easy to use.
• Compact (array handling is Fortran 90‐like).
• Shorter program development time than traditional programming languages such as
FORTRAN and C.
• Can be converted into C code via MATLAB compiler for better efficiency.
• Many applications‐ specific toolboxes available.
• Coupled with Maple for symbolic computations.
• On shared‐memory parallel computers such as the SGI Origin2000, certain operations
processed in parallel autonomously when computation load warrants.
KEY FEATURES:-
• High level language for technical computing.
• Development environment for managing code, files, and data.
• Interactive tools for iterative exploration, design and problem solving.
• Mathematical functions for linear algebra, statistics, Fourier analysis, filtering, optimization,
and numerical integration
• 2‐D and 3‐D graphical functions for visualizing data.
• Tools for building custom graphical user interfaces.
• Functions for integrating MATLAB based algorithm with external application and languages,
such as C, C++, FORTRAN, Java, and Microsoft Excel.
2

5. EXAMPLES:-
• Matrix computation and linear algebra.
• Solving nonlinear equation.
• Numerical solution of differential equation.
• Mathematical optimization.
• Statistical and data analysis.
• Signal Processing.
• Modeling of dynamical systems.
• Solving partial differential equation.
• Simulation of Engg. Systems.
USES IN ENGG. COMPANIES:‐
• Numerical analysis
• Signal and system.
• Modeling of dynamical systems.
• Automatic control.
BASIC COURSES:‐
• Automatic control advanced course.
• Hybrid and embedded.
• Control system.
• Chemical process control.
• Control process control.
• Signal theory.
• Digital signal processing.
• Adaptive signal processing.
• Signal processing project.
• Communication theory.
• Advance communication theory.
3

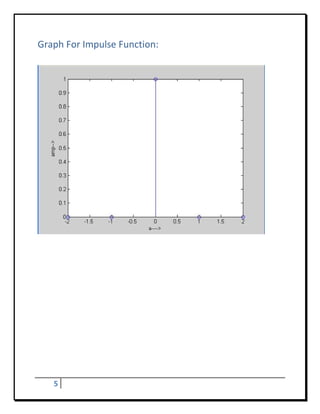
6. Program - 1
To Develop Elementary Signal For Impulse Function
Program:
a=[‐2;1;2]
b=[zeros(1,2),ones(1,1),zeros(1,2)]
stem(a,b)
xlabel(‘a‐‐‐‐>’)
ylabel(‘amp‐‐‐>’)
Result:
a= ‐2 ‐1 0 1 2
b= 0 0 1 0 0
4

7. Graph For Impulse Function:
5

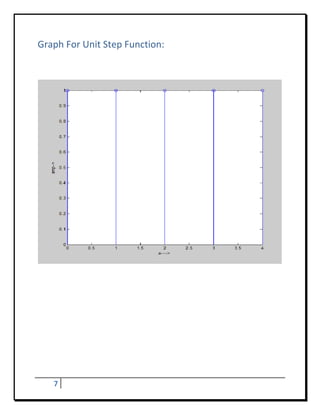
8. Program - 2
To Develop Elementary Signal For Unit Step Function
Program:
n=input(’enter the value of n’)
a=[1:1:n]
b=[ones,n]
subplotes
stem(a,b)
xlabel(‘n…..>’)
ylabel(‘amplitude’)
Result of unit step function:
Enter the value of n
n=5
a=0 1 2 3 4
b= 1 1 1 1 1
6

9. Graph For Unit Step Function:
7

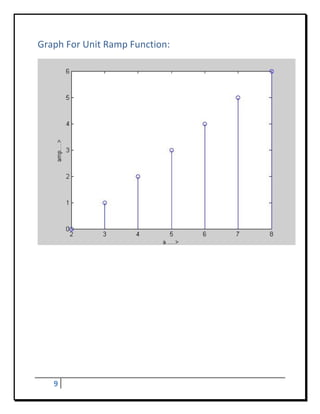
10. Program - 3
To Develop Elementary Signal For Unit Ramp Function
Program:
a=[2:1:8]
b=[0;1;6]
subplot
stem(a,b)
xlabel(‘n.’)
ylabel(‘amp….’)
Result of unit ramp function:
a=2 3 4 5 6 7 8
b= 0 1 2 3 4 5 6
8

11. Graph For Unit Ramp Function:
9

12. Program - 4
To Develop Exponential Function Of (Given) Sequence
Program:
n=input(‘enter the value of n’)
a=input(‘enter the value of a’)
t=[0:1:n]
y=exp(a*t)
subplot
stem(t,y)
xlabel(‘a’)
ylabel(‘n’)
Result of exponential:
Enter the value of n10
n= 10
enter the value of a0.5
a= 0.5000
t=0 1 2 3 4 5 6 7 8 9 10
y=columns 1 through 10
1.0000 1.6487 2.7183 4.4817 7.3891 12.1825 20.0855 33.1155 54.5982 90.0171
Column11
148.4132
10

13. Graph For Exponential Function:
11

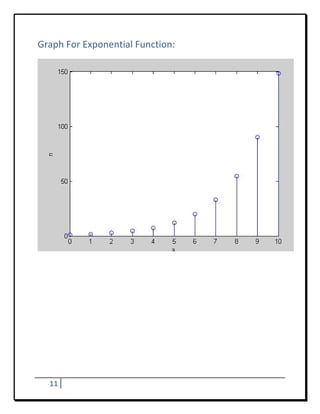
14. Program - 5
To Develop Elementary Signal For Real Value
Program:
n=[0,1,2,3,4,5]
a=[0.5]
y=a.^n
subplot
stem(n,y)
xlabel(‘n…..’)
ylabel(‘a’)
Result of Real Value No.:
n= 0 1 2 3 4 5
a= 0.5000
y = 1.0000 0.5000 0.2500 0.1250 0.0625 0.0313
12

15. Graph For Real Value Function:
13

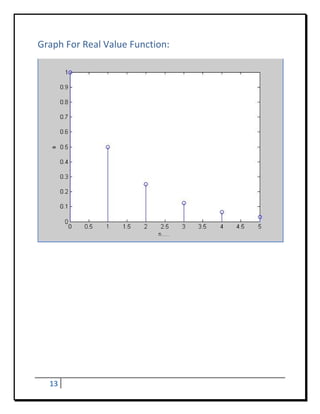
16. Program - 6
To Develop Elementary Signal For Shifting Program:
a=[‐3:1:3]
b=[1.2.3.2.1.1.2]
subplot(3,1,1)
stem(a,b)
xlabel(‘n‐‐‐‐>’)
ylabel(‘amp‐‐‐>’)
a=‐a
subplot(3,1,2)
stem(a,b)
xlabel(‘n‐‐‐‐>’)
ylabel(‘amp‐‐‐>’)
Result:
a = ‐3 ‐2 ‐1 0 1 2 3
b = 1 2 3 2 1 1 2
a = 3 2 1 0 ‐1 ‐2 ‐3
14

17.
Graph For Shifting Function:
15

18.
Program - 7
To Develop Elementary Signal For Addition Of Two
Sequences
Program:
n=[‐3:1:3]
b=[2,3,0,1,3,2,1]
subplot(5,1,1)
stem(n,b)
xlabel('n….>')
ylabel('amplitude')
title('input of signal b')
a=[3,4,5,6,7,8,9]
subplot(5,1,3)
stem(n,b)
ylabel('amplitude')
title('input of signal a')
z=b+a
subplot(5,1,5)
stem(n,a)
xlabel('n….>')
ylabel('amplitude')
title('addition of two signal is z(n)')
Result of Addition:
2 3 0 1 3 2 1
a = 3 4 5 6 7 8 9
z = 5 7 5 7 10 10 10
16

19. Graph For Addition Function:
17

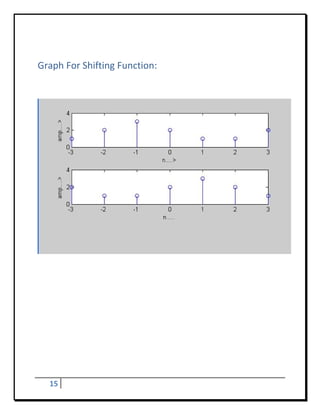
20. Program - 8
To Develop Elementary Signal For Multiplication Of Two
Sequences
Program:
n=[‐2:1:3]
x=[1,2,3,4,5,6]
subplot(3,1,1)
stem(n,x)
xlabel('n‐‐‐‐>')
ylabel('amp‐‐‐>')
y=[2]
z=(x*y)
subplot(3,1,2)
stem(n,z)
xlabel('n‐‐‐‐>')
ylabel('amp‐‐‐>')
Result:
n = ‐2 ‐1 0 1 2 3
x = 1 2 3 4 5 6
y = 2
z = 2 4 6 8 10 12
18

21. Graph For Multiplication Function:
19

22. Program - 9
To Develop The Elementary Signal For Convolution Of
Two Sequences
Program:
X=input(‘enter the value of x’)
h=input(‘enter the value of h’)
y=conv(x,h)
subplot(3,1,1)
stem(x)
xlabel(‘n….>’)
ylabel(‘amplitude….>’)
subplot(3,1,2)
stem(h)
xlabel(‘n….>’)
ylabel(‘amplitude….>’)
subplot(3,1,3)
stem(y)
xlabel(‘n….>’)
ylabel(‘amplitude….>’)
20

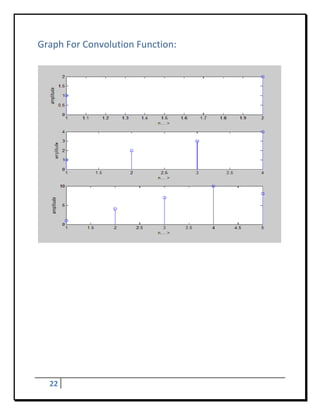
23. Result of convolution:
Enter the sequence of x[1,2]
X=1 2
Enter the sequence of h[1,2,3,4]
h = 1 2 3 4
y = 1 4 7 10 8
21

24. Graph For Convolution Function:
22

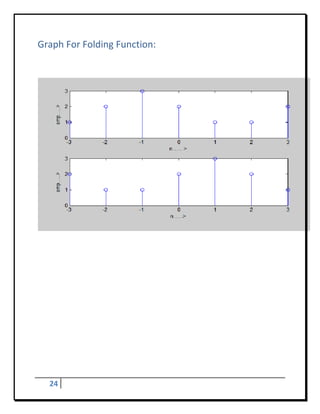
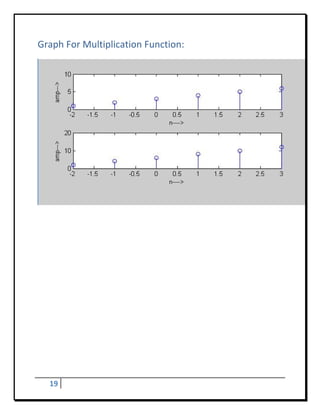
25. Program - 10
To Develop Elementary Signal For Folding
Program:
a=[‐3:1:3]
b=[1,2,3,2,1,1,2]
subplot(3,1,1)
stem(a,b)
xlabel(‘n….. >’)
ylabel(‘amp…..>’)
a= ‐a
subplot(3,1,2)
stem(a,b)
xlabel(‘n…..>’)
ylabel(‘amp…..>’)
Result of Folding:
a= ‐3 ‐2 ‐1 0 1 2 3
b= 1 2 3 2 1 1 2
a= 3 2 1 0 ‐1 ‐2 ‐3
23

26. Graph For Folding Function:
24