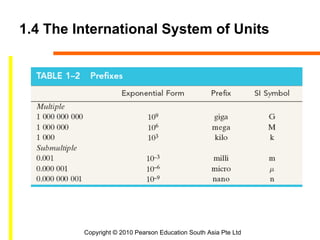
This document provides an overview of engineering mechanics and statics concepts. It discusses the three branches of mechanics, including rigid-body mechanics which deals with both statics and dynamics. The fundamentals of statics are presented, including basic quantities like length, mass and time. Newton's laws of motion and gravitational attraction are also covered. The document outlines the International System of Units and procedures for numerical calculations and general problem solving in mechanics.