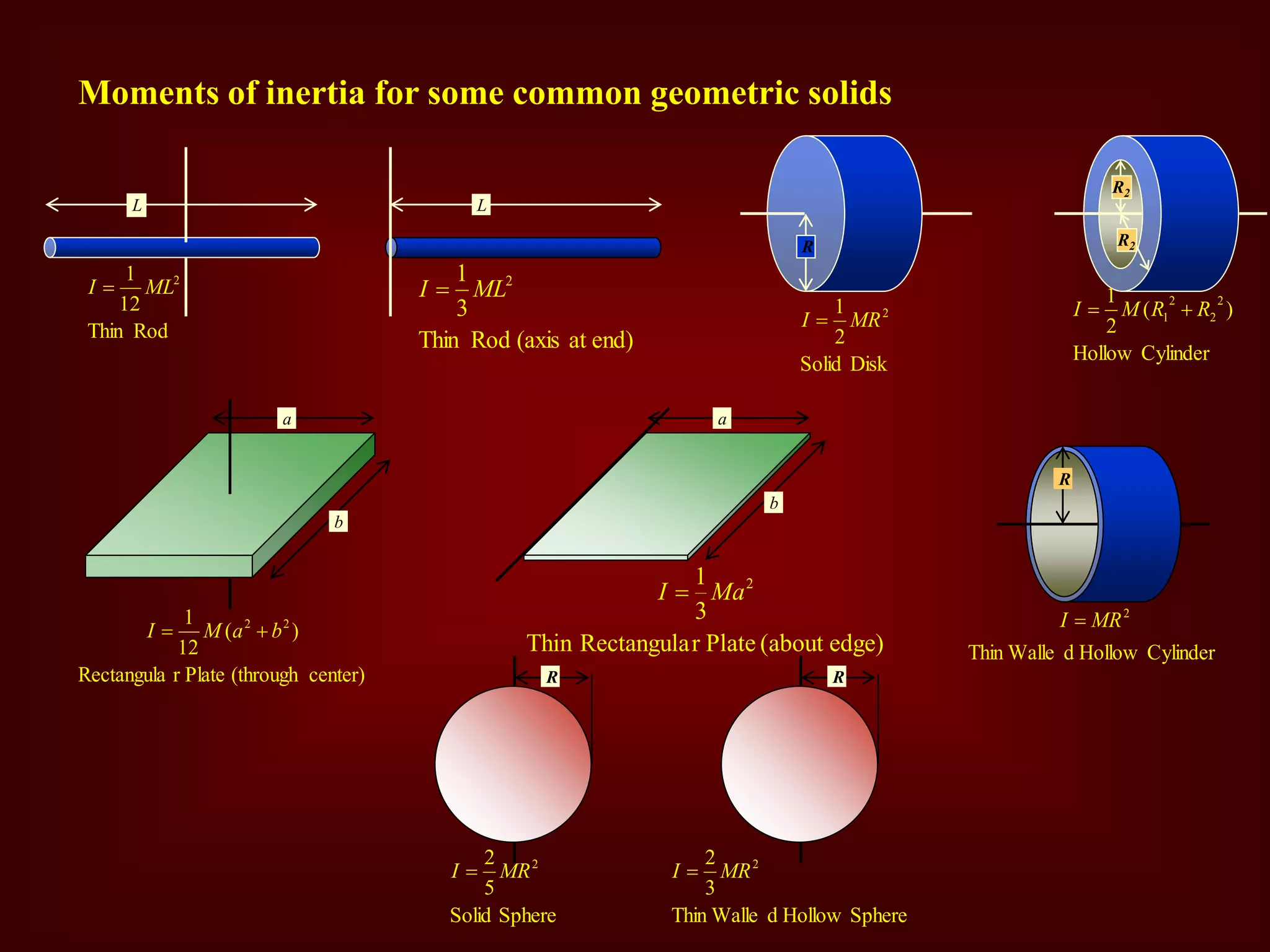
This document discusses moment of inertia, including its definition as a measure of an object's resistance to changes in angular acceleration. Key concepts covered include the parallel axis theorem, radius of gyration, calculating moments of inertia for composite bodies, and applications such as how moment of inertia affects how easily a wheel can be sped up. Formulas are provided for moments of inertia of common shapes like rods, disks, hollow cylinders, and spheres. Methods are described for finding the moment of inertia of composite objects by dividing them into simple shapes and summing the individual moments of inertia.

1. SACRED HEART DEGREE COLLEGE
MOMENT OF INERTIA
BY
SATYAM SRIVASTAVA
(M.Sc. second year math)

2. Contents
• Moment of Inertia of a body
• Parallel Axis Theorem
• Radius of Gyration
• Moment of Inertia of Composite Bodies
• Applications of moment of inertia

3. Moment and Angular Acceleration
• When M  0, rigid body experiences
angular acceleration
• Relation between M and a is analogous to
relation between F and a
a
I
ma 
 M
,
F
Moment of Inertia
Mass = Resistance

4. Moment of Inertia
• This mass analog is called the
moment of inertia, I, of the object
– r = moment arm
– SI units are kg m2


m
dm
r
I 2

 dz
dy
dx
r
I 2

dV
r
I
dV
dm



2
:
density
volume
the
is
where
,
Using




5. Shell Element
Disk Element
dy
z
y
dV )
2
( 

dz
y
dV )
( 2



6. Example
)
2
( h
dr
r
dV
dm 

 

)
(
2
1
2
2 2
2
4
0
3
2
h
R
R
h
R
dr
r
h
dm
r
I
R
m



 


 

h
R
m 2



2
2
1
R
m
Iz 

7. Example
dy
x
dV
dm )
( 2


 

2
2
1
R
m
I 
dy
x
x
dy
x
R
m
Iy
4
2
2
2
2
1
]
)
(
[
2
1
2
1


 


3
2
slug/ft
5
, 
 
y
x
2
1
0
8
1
0
4
slug.ft
873
.
0
2
)
5
(
2


 
 dy
y
dy
x
Iy



9. Rod
Thin
12
1 2
ML
I 
L
end)
at
(axis
Rod
Thin
3
1 2
ML
I 
L
Disk
Solid
2
1 2
MR
I 
R
Cylinder
Hollow
)
(
2
1 2
2
2
1 R
R
M
I 

R2
R2
Cylinder
Hollow
d
Thin Walle
2
MR
I 
R
a
b
center)
(through
Plate
r
Rectangula
)
(
12
1 2
2
b
a
M
I 

a
b
edge)
(about
Plate
r
Rectangula
Thin
3
1 2
Ma
I 
Sphere
Solid
5
2 2
MR
I 
R
Sphere
Hollow
d
Thin Walle
3
2 2
MR
I 
R
Moments of inertia for some common geometric solids

10. Parallel Axis Theorem
• The moment of inertia about any axis parallel to
and at distance d away from the axis that
passes through the centre of mass is:
• Where
– IG= moment of inertia for mass centre G
– m = mass of the body
– d = perpendicular distance between the parallel axes.
2
md
I
I G
O 


11. Radius of Gyration
Frequently tabulated data related to moments of inertia will be
presented in terms of radius of gyration.
m
I
k
or
mk
I 
 2

12. Mass Center



m
m
y
y
~
Example
ft
5
.
1
)
2
.
32
/
10
(
)
2
.
32
/
10
(
)
2
.
32
/
10
(
2
)
2
.
32
/
10
(
1
~







m
m
y
y
10 Ib

13. Moment of Inertia of Composite bodies
1. Divide the composite area into simple body.
2. Compute the moment of inertia of each simple body about its
centroidal axis from table.
3. Transfer each centroidal moment of inertia to a parallel reference axis
4. The sum of the moments of inertia for each simple body about the
parallel reference axis is the moment of inertia of the composite
body.
5. Any cutout area has must be assigned a negative moment; all others
are considered positive.

14. Applications of Moment of Inertia
1. A wheel in which most of the mass lie near the axle is easier to
speed up in comparison to the other wheel in which equal mass
is spread over a larger diameter.