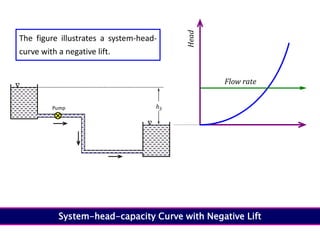
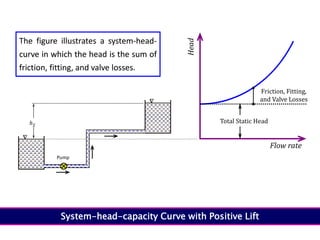
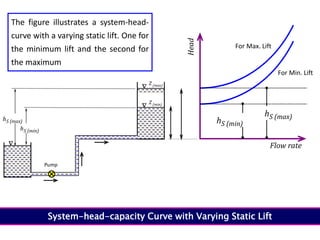
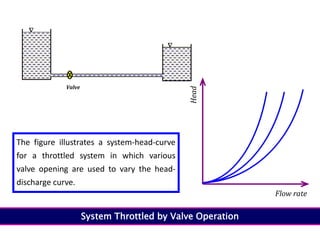
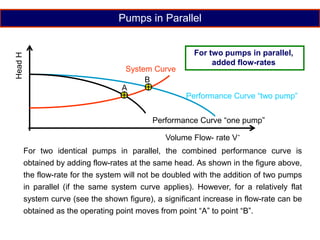
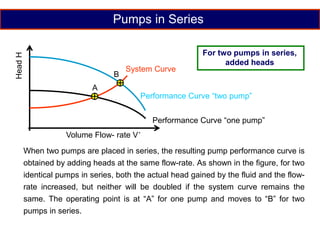
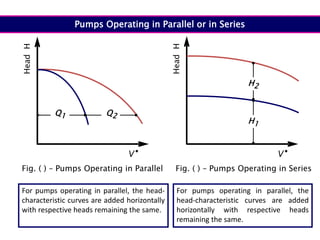
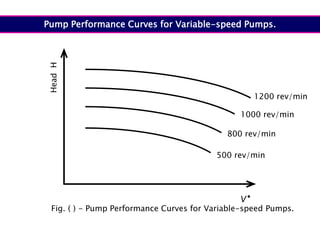
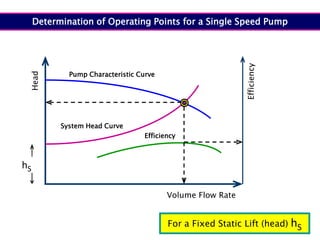
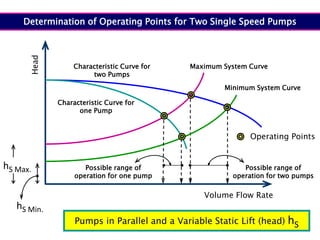
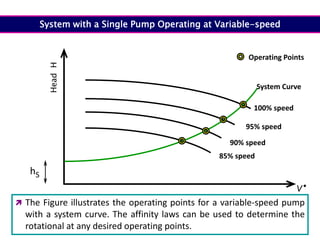
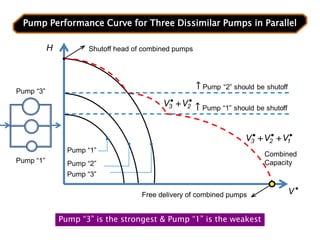
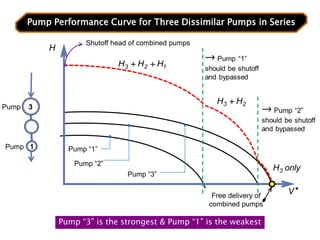
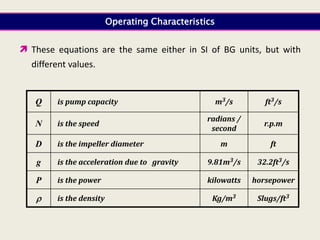
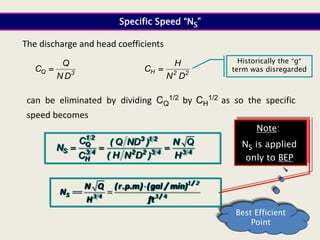
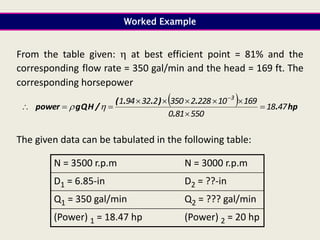
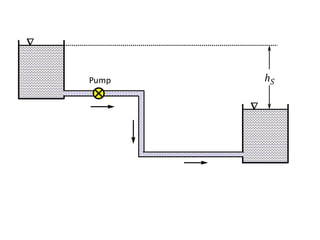
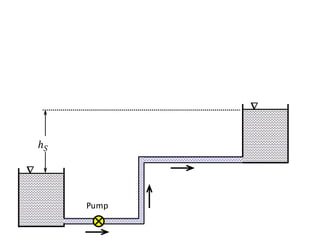
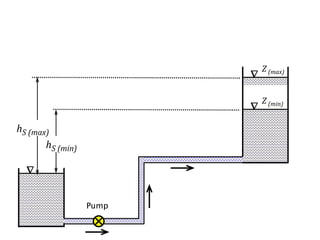
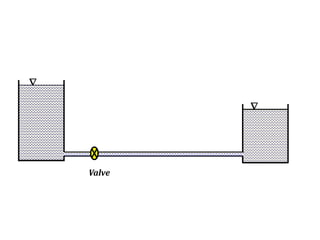
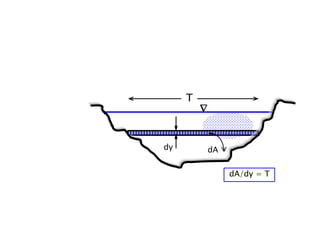
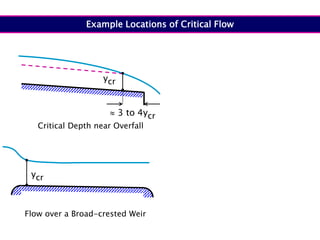
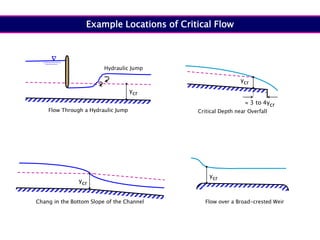
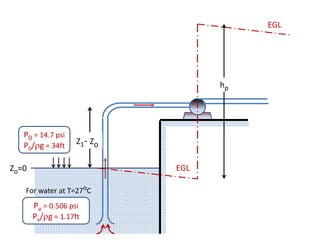
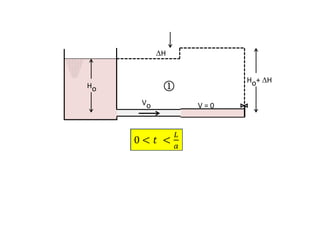
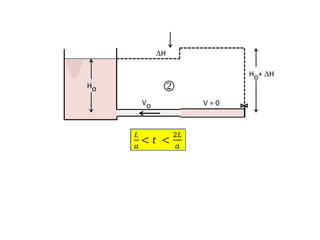
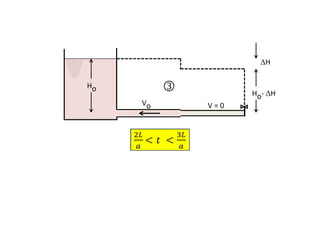
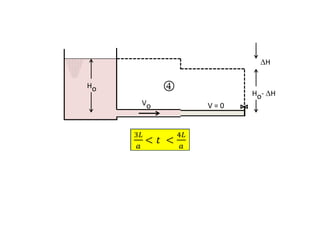
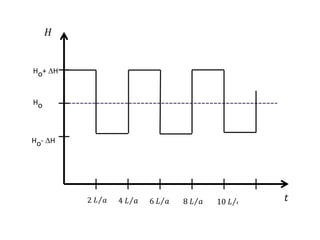
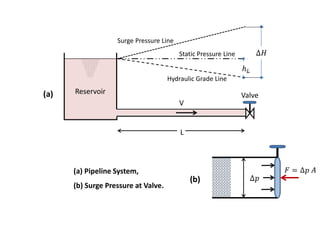
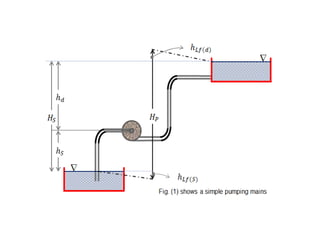
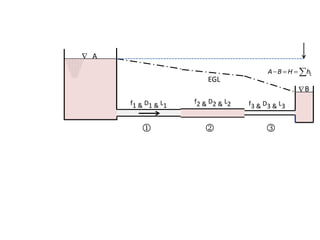
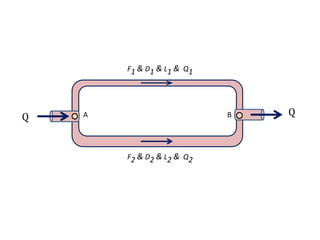
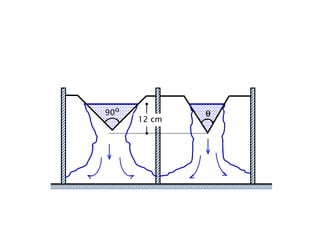
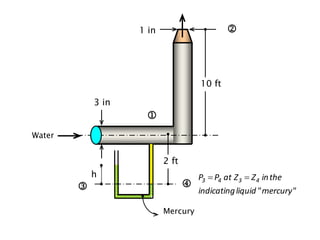
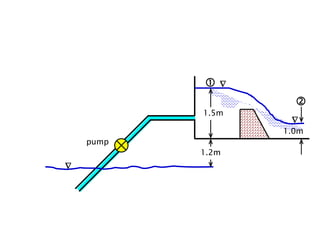
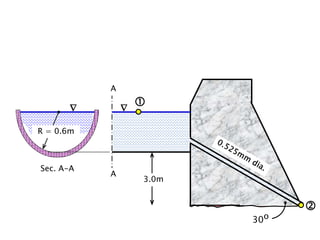
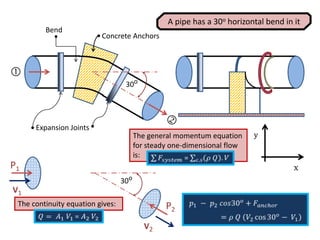
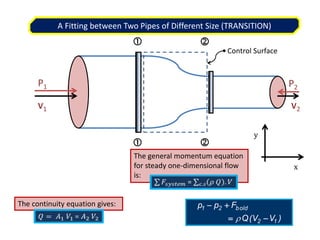
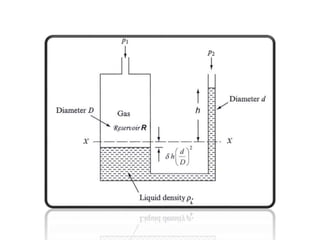
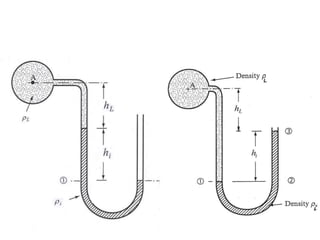
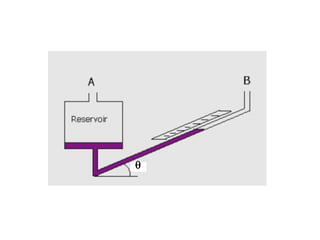
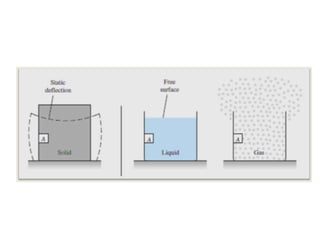
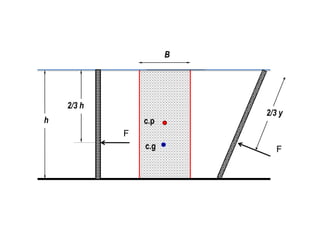
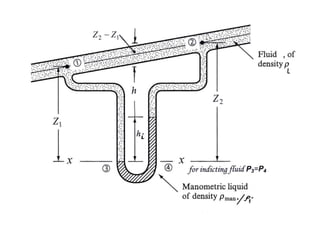
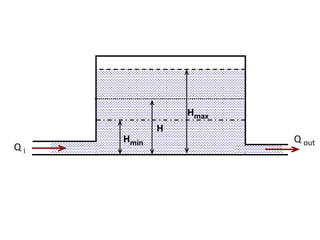
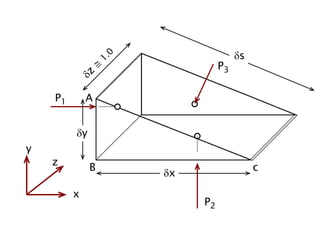
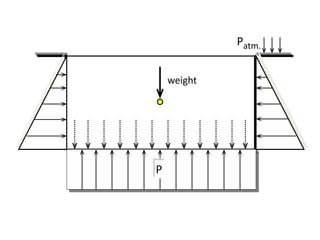
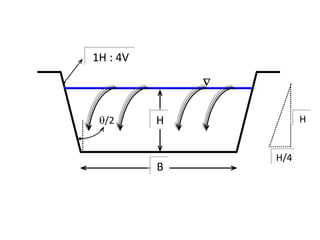
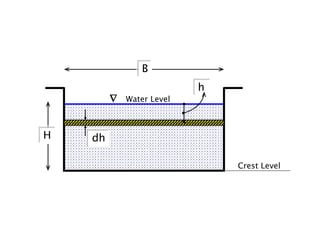
When adding additional pumps in parallel or series, care must be taken to avoid damage to individual pumps. Pumps should be shut off if their shutoff head is exceeded. If pumps are identical, they can all remain on. When combining pumps, their performance curves are added horizontally for parallel operation and vertically for series operation. This determines the combined operating point where it intersects the system curve.