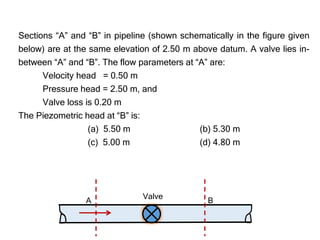
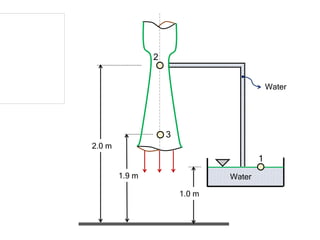
The document discusses several fluid mechanics problems involving pipes, valves, pumps, and Venturi meters. It provides the relevant equations, diagrams, and step-by-step workings to calculate pressure, velocity, discharge, and other flow parameters for each problem.
The document also contains an Arabic passage discussing philosophical concepts like thinking outside the box and challenging preconceived notions.