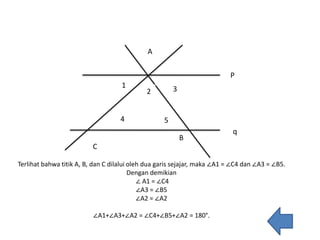
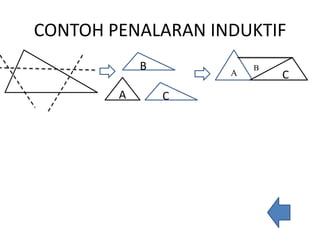
Dokumen ini membahas konsep kemampuan penalaran matematis, mencakup definisi, jenis-jenis penalaran (deduktif dan induktif), serta indikator dan keuntungan dari penalaran matematis bagi siswa. Penalaran deduktif melibatkan penarikan kesimpulan dari fakta yang dianggap benar, sementara penalaran induktif berdasarkan pengetahuan tentang hal khusus. Siswa yang menggunakan penalaran ini dapat memperbaiki kepercayaan diri dan pemahaman mereka dalam matematika.

1. Bismillahirrohmanirrohim..

2. Pertemuan ke-10
LILIS SURYATI
NIM : 0903646
INTERES MATEMATIKA

3. PENALARAN MATEMATIS
• Menurut kamus Bahasa Indonesia masing-masing
katanya, kemampuan berasal dari kata mampu yang
berarti kuasa, bisa, sanggup melakukan sesuatu.
Berarti kemampuan dapat diartikan kesanggupan.
• Penalaran yang berarti cara (perihal) menggunakan
nalar, pemikiran atau cara berpikir logis dalam
mengembangkan pikiran dari beberapa fakta.

4. PENGERTIAN PENALARAN
• Menurut Shurter dan Pierce
(Armiati, 2011) mendefinisikan
penalaran sebagai proses penarikan
kesimpulan logis berdasarkan fakta
dan sumber yang relevan.
• Keraf (Yuliana, 2011:14), menyatakan
bahwa penalaran (reasoning) adalah
proses berfikir yang berusaha
menghubung-hubungkan fakta-fakta
yang diketahui menuju kepada suatu

5. Contoh penalaran

6. Macam-macam penalaran
• Dilihat dari prosesnya, penalaran terdiri dari
atas penalaran deduktif dan penalaran
induktif
Penalaran deduktif
Penalaran induktif

7. • Penalaran deduktif menurut Jacobs
(Suhandri, 2011) suatu cara penarikan
kesimpulan dari pernyataan atau fakta-fakta
yang dianggap benar dengan menggunakan
logika.

8. Contoh penalaran deduktif
n
1 2
p
4 3
5 6
q
8 7
Pada gambar diatas, karena dua garis sejajar p dan q dipotong oleh garis n
maka sudut-sudut dalam bersebrangan sama, dengan demikian
∠ 4 = ∠ 6 dan ∠3 = ∠ 5.

9. A
P
1 3
2
4 5
q
B
C
Terlihat bahwa titik A, B, dan C dilalui oleh dua garis sejajar, maka ∠A1 = ∠C4 dan ∠A3 = ∠B5.
Dengan demikian
∠ A1 = ∠C4
∠A3 = ∠B5
∠A2 = ∠A2
∠A1+∠A3+∠A2 = ∠C4+∠B5+∠A2 = 180°.

10. Penalaran induktif
• Menurut Kusumah
(Sobariah, 2011:10)Penalaran induktif
adalah proses berpikir berupa penarikan
kesimpulan yang umum atas dasar
pengetahuan tentang hal khusus yang
dimulai dari sekumpulan fakta yang ada

11. CONTOH PENALARAN INDUKTIF
B B
A C
A C

12. Indikator penalaran
• Menurut Pors (Opik, 2011) indikator dari penalaran adalah :
• 1. Memberikan alasan mengapa sebuah jawaban atau pendekatan
terhadap suatu masalah adalah masuk akal
• 2. Membuat dan mengevaluasi kesimpulan umum berdasarkan
penyelidikan dan penelitian
• 3. Meramalkan dan menggambarkan kesimpulan atau putusan dari
informasi yang sesuai
• 4. Menganalisis pernyataan-pernyataan dan memberikan contoh
yang dapat mendukung atau bertolak belakang
• 5. Mempertimbangkan validitas dari argumen yang menggunakan
berpikir deduktif dan induktif
• 6. Menggunakan data yang mendukung untuk menjelaskan
mengapa cara yang digunakan serta jawaban benar.

13. Keuntungan penalaran matematis
• Siswa diberi kesempatan untuk menggunakan keterampilan
bernalarnya dalam melakukan pendugaan-pendugaan berdasarkan
pengalamanya sendiri, sehingga siswa akan lebih mudah
memahaminya.
• Siswa dituntut untuk menggunakan kemampuan bernalarnya, maka
akan mendorong mereka untuk melakukan guessing atau dugaan-
dugaan. Hal ini akan menimbulkan rasa percaya diri dan
menghilangkan rasa takut salah ketika siswa dimintai untuk menjawab
pertanyaan yang diajukan oleh guru.

14. • Membantu siswa untuk memahami nilai balikan yang
negatif dalam memutuskan jawaban, artinya siswa perlu
memahami tebakan yang salah dan menghilangkan
kemungkinan yang pasti dengan berbagai pertimbangan
yang lebih jauh dan dapat melihat informasi yang sangat
bernilai. Siswa juga perlu menghargai bahwa keefektifan
suatu tebakan tergantung pada banyaknya kemungkinan
yang dihilangkan.
• Secara khusus, dalam matematika siswa harus memahami
penalaran induktif (pendugaan) dan penalaran deduktif
(pembuktian logis) memainkan peranan yang sangat
penting.

15. • SEKIAN
• DAN
• TERIMAKASIH