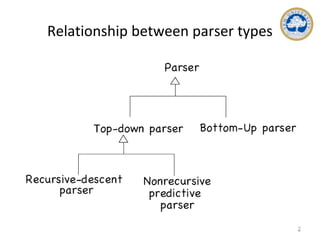
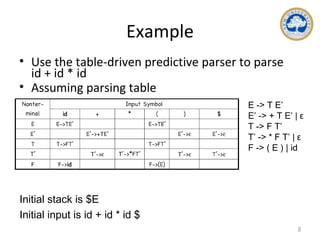
This document discusses top-down parsing and different types of top-down parsers, including recursive descent parsers, predictive parsers, and LL(1) grammars. It explains how to build predictive parsers without recursion by using a parsing table constructed from the FIRST and FOLLOW sets of grammar symbols. The key steps are: 1) computing FIRST and FOLLOW, 2) filling the predictive parsing table based on FIRST/FOLLOW, 3) using the table to parse inputs in a non-recursive manner by maintaining the parser's own stack. An example is provided to illustrate constructing the FIRST/FOLLOW sets and parsing table for a sample grammar.

1. Top-Down Parsing
1

2. Relationship between parser types
2

3. Recursive descent
• Recursive descent parsers simply try to build a
top-down parse tree.
• It would be better if we always knew the
correct action to take.
• It would be better if we could avoid recursive
procedure calls during parsing.
3

4. Predictive parsers
• A predictive parser always knows which
production to use, ( to avoid backtracking )
• Example: for the productions
•
stmt -> if ( expr ) stmt else stmt
| while ( expr ) stmt
| for ( stmt expr stmt ) stmt
• a recursive descent parser would always know
which production to use, depending on the input
token.
4

5. Transition diagrams
• Transition diagrams can describe recursive parsers,
just like they can describe lexical analyzers,
• (but the diagrams are slightly different.)
• Construction:
1. Eliminate left recursion from G
2. Left factor G
3. For each non-terminal A, do
1. Create an initial and final (return) state
2. For each production A -> X1 X2 … Xn, create a path from
the initial to the final state with edges X1 X2 … Xn.
5

6. Example transition diagrams
• An expression
grammar with left
recursion
• With ambiguity
• E -> E+T | T
• T -> T*F | F
• F -> (E) | id
6
Corresponding transition
diagrams:
Eliminating the ambiguity
E -> T E’
E’ -> + T E’ | ε
T -> F T’
T’ -> * F T’ | ε
F -> ( E ) | id

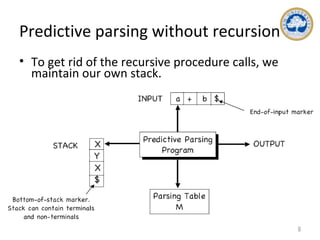
7. The parsing table and parsing program
• The table is a 2D array M[A,a] where A is a
nonterminal symbol and a is a terminal or $.
• At each step, the parser considers the top-of-
stack symbol X and input symbol a:
If both are $, accept
If they are the same (nonterminals), pop X, advance
input
If X is a nonterminal, consult M[X,a].
– If M[X,a] is “ERROR” call an error recovery routine.
Otherwise, if M[X,a] is a production of the
grammar X -> UVW, replace X on the stack with WVU
(U on top)
7

8. Predictive parsing without recursion
• To get rid of the recursive procedure calls, we
maintain our own stack.
8

9. Example
• Use the table-driven predictive parser to parse
id + id * id
• Assuming parsing table
9
Initial stack is $E
Initial input is id + id * id $
E -> T E’
E’ -> + T E’ | ε
T -> F T’
T’ -> * F T’ | ε
F -> ( E ) | id

10. Building a predictive parse table
• The construction requires two functions:
• 1. FIRST
• 2. FOLLOW
10

11. For First
• For a string of grammar symbols α, FIRST(α) is
the set of terminals that begin all possible
strings derived from α. If α =*
> ε, then ε is also
in FIRST(α).
• E -> T E’
• E’ -> + T E’ | ε
• T -> F T’
• T’ -> * F T’ | ε
• F -> ( E ) | id
11
FIRST(E) = FIRST (T) = FIRST (F) = {( , id }
FIRST(E’) = {+ , ε}
FIRST(T) = {( , id}
FIRST(T’) = { *, ε}
FIRST(F) = {( , id }

12. For Follow
• FOLLOW(A) for non terminal A is the set of terminals
that can appear immediately to the right of A in some
sentential form. If A can be the last symbol in a
sentential form, then $ is also in FOLLOW(A).
• E -> T E’
• E’ -> + T E’ | ε
• T -> F T’
• T’ -> * F T’ | ε
• F -> ( E ) | id
12
Follow (E) = { ) , $ }
Follow (E’) = Follow (E)= { ) ,$ }
Follow (T) = { +, Follow (E)}= {+ , ) , $}
Follow (T’) = {+, ) ,$}
Follow ( F) = {*, +, ), $ }

13. How to compute FIRST(α)
1. If X is a terminal, FIRST(X) = X.
2. Otherwise (X is a nonterminal),
1. 1. If X -> ε is a production, add ε to FIRST(X)
2. 2. If X -> Y1 … Yk is a production, then place a in
FIRST(X) if for some i, a is in FIRST(Yi) and Y1…Yi-1 =*
> ε.
• Given FIRST(X) for all single symbols X,
• Let FIRST(X1…Xn) = FIRST(X1)
• If ε FIRST(X∈ 1), then add FIRST(X2), and so on…
13

14. How to compute FOLLOW(A)
• Place $ in FOLLOW(S) (for S the start symbol)
• If A -> α B β, then FIRST(β)-ε is placed in
FOLLOW(B)
• If there is a production A -> α B or a
production A -> α B β where β =*
> ε, then
everything in FOLLOW(A) is in FOLLOW(B).
• Repeatedly apply these rules until no FOLLOW
set changes.
14

15. Example FIRST and FOLLOW
• For our favorite grammar:
E -> TE’
E’ -> +TE | ε
T -> FT’
T’ -> *FT’ | ε
F -> (E) | id
• What is FIRST() and FOLLOW() for all
nonterminals?
15

16. Parse table construction with
FIRST/FOLLOW
• Basic idea: if A -> α and a is in FIRST(α), then we expand A to α any time
the current input is a and the top of stack is A.
• Algorithm:
• For each production A -> α in G, do:
• For each terminal a in FIRST(α) add A -> α to M[A,a]
• If ε FIRST(α), for each terminal b in FOLLOW(A), do:∈
• add A -> α to M[A,b]
• If ε FIRST(α) and $ is in FOLLOW(A), add A -> α to M[A,$]∈
• Make each undefined entry in M[ ] an ERROR
16

17. Example predictive parse table construction
• For our favorite grammar:
E -> TE’
E’ -> +TE | ε
T -> FT’
T’ -> *FT’ | ε
F -> (E) | id
• What the predictive parsing table?
17

18. LL(1) grammars
• The predictive parser algorithm can be applied to
ANY grammar.
• But sometimes, M[ ] might have multiply defined
entries.
• Example: for if-else statements and left factoring:
stmt -> if ( expr ) stmt optelse
optelse -> else stmt | ε
• When we have “optelse” on the stack and “else”
in the input, we have a choice of how to expand
optelse (“else” is in FOLLOW(optelse) so either
rule is possible)
18

19. LL(1) grammars
• If the predictive parsing construction for G leads to a
parse table M[ ] WITHOUT multiply defined entries,
we say “G is LL(1)”
19
1 symbol of lookahead
Leftmost derivation
Left-to-right scan of the input

20. LL(1) grammars
• Necessary and sufficient conditions for G to
be LL(1):
• If A -> α | β
1. There does not exist a terminal a such that
a FIRST(α) and a FIRST(∈ ∈ β)
2. At most one of α and β derive ε
3. If β =*
> ε, then FIRST(α) does not intersect with
FOLLOW(β).
20
This is the same as saying the
predictive parser always
knows what to do!

21. Model of a non recursive predictive parser.
21
a + b $a + b $
XX
YY
ZZ
$$
Input bufferInput buffer
stackstack
Predictive parsing
program/driver
Predictive parsing
program/driver
Parsing Table MParsing Table M

22. Moves made by predictive parser on input id + id * id
STACKSTACK INPUTINPUT OUTPUTOUTPUT
$$EE
$$EE' T' T
$$EE' T' F' T' F
$$EE' T'' T' idid
$$EE' T'' T'
$$EE''
$$EE' T' T ++
$$EE' T' T
$$EE' T' F' T' F
$$EE' T'' T' idid
$$EE' T'' T'
$$EE' T' F' T' F **
$$EE' T' F' T' F
$$EE' T'' T' idid
$$EE' T'' T'
$$EE''
$$
idid ++ idid ** idid$$
idid ++ idid ** idid$$
idid ++ idid ** idid$$
idid ++ idid ** idid$$
++ idid ** idid$$
++ idid ** idid$$
++ idid ** idid$$
idid ** idid$$
idid ** idid$$
idid ** idid$$
** idid$$
** idid$$
idid$$
idid$$
$$
$$
$$
EE →→ TT EE''
TT →→ F TF T''
FF →→ idid
TT'' →→ εε
EE'' →→ ++ TT EE''
TT →→ F TF T''
FF →→ idid
TT'' →→ ** F TF T''
FF →→ idid
TT'' →→ εε
EE'' →→ εε
22

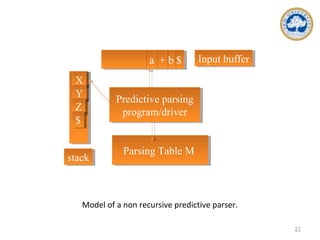
23. Nonrecursive Predictive Parsing
• 1. If X = a = $, the parser halts and announces successful completion of parsing.
• 2. If X = a ≠ $, the parser pops X off the stack and advances the input pointer to the next
input symbol.
• 3. If X is a nonterminal, the program consults entry M[X, a] of the parsing table M. This
entry will be either an X-production of the grammar or an error entry. If, for example, M[X, a]
= {X → UVW}, the parser replaces X on top of the stack by WVU (with U on top). As output,
we shall assume that the parser just prints the production used; any other code could be
executed here. If M[X, a] = error, the parser calls an error recovery routine.
23

24. Parsing table M for grammar
NONTER-NONTER-
MINALMINAL
INPUT SYMBOLINPUT SYMBOL
IdId ++ ** (( )) $$
EE
EE''
TT
TT''
FF
EE →→ TE'TE'
TT →→ FT'FT'
FF →→ idid
E'E' →→ ++TE'TE'
T'T' →→ εε T'T' →→ **FT'FT'
EE →→ TE'TE'
TT →→ FT'FT'
FF →→ ((EE))
E'E' →→ εε
T'T' →→ εε
E'E' →→ εε
T'T' →→ εε
24

25. Top-down parsing recap
• RECURSIVE DESCENT parsers are easy to build, but inefficient,
and might require backtracking.
• TRANSITION DIAGRAMS help us build recursive descent
parsers.
• For LL(1) grammars, it is possible to build PREDICTIVE
PARSERS with no recursion automatically.
 Compute FIRST() and FOLLOW() for all nonterminals
 Fill in the predictive parsing table
 Use the table-driven predictive parsing algorithm
25