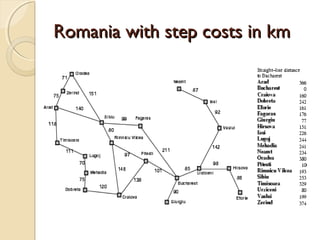
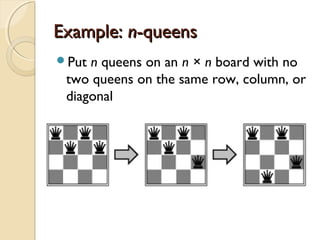
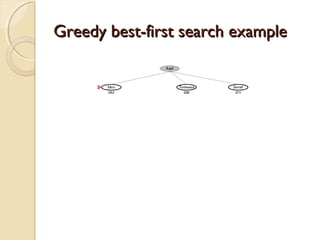
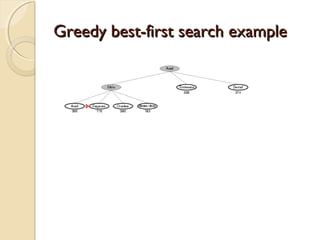
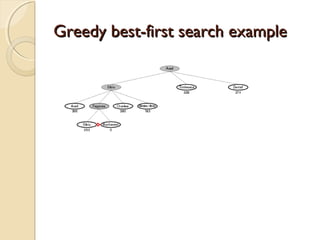
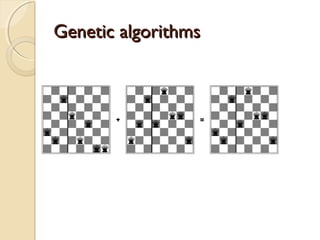
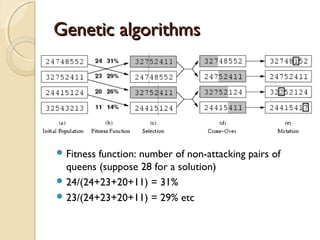
1) The document discusses various search algorithms including uninformed searches like breadth-first search as well as informed searches using heuristics. 2) It describes greedy best-first search which uses a heuristic function to select the node closest to the goal at each step, and A* search which uses both path cost and heuristic cost to guide the search. 3) Genetic algorithms are introduced as a search technique that generates successors by combining two parent states through crossover and mutation rather than expanding single nodes.

1. Chapter 4Chapter 4
Informed search & ExplorationInformed search & Exploration
CSE 4701

2. Review: Tree searchReview: Tree search
A search strategy is defined by picking the
order of node expansion
Uninformed search strategies use only the
information available in the problem definition
◦ Breadth-first search
◦ Uniform-cost search
◦ Depth-first search
◦ Depth-limited search
◦ Iterative deepening search

3. HeuristicsHeuristics

4. Heuristics examplesHeuristics examples
A heuristic function at a node n is an estimate
of the optimum cost from the current node to
a goal. Denoted by h(n)
h(n)= estimated cost of the cheapest path from
node n to a goal node.
Example: want path from Dhaka to Chittagong
Heuristics for Chittagong may be straight line
distance between Dhaka and Chittagong

5. Heuristic examplesHeuristic examples

6. Best-first searchBest-first search
 Idea: use an evaluation function f(n) for each node
◦ estimate of "desirability“
1. Greedy Best-First Search
2. A*
search

7. Romania with step costs in kmRomania with step costs in km

8. Greedy best-first searchGreedy best-first search
Evaluation function f(n) = h(n) (heuristic)
= estimate of cost from n to goal
e.g., hSLD(n) = straight-line distance from n
to Bucharest
Greedy best-first search expands the
node that appears to be closest to goal

9. Greedy best-first search exampleGreedy best-first search example

10. Greedy best-first search exampleGreedy best-first search example

11. Greedy best-first search exampleGreedy best-first search example

12. Greedy best-first search exampleGreedy best-first search example

13. But is this solution optimal?
No, because instead of using the via Sibiu and
fagaras to Bucharest, if we follow the path
through Rimmicu Vilcea and Pitesti, then we
have to go 32 km less than the first path.
This shows why the algorithm is called
“greedy”- at every step it tries to get as close
to the goal as it can.

14. Drawbacks of greedy searchDrawbacks of greedy search
Minimizing h(n) is susceptible to false
starts. Consider the problem of getting
from Iasi to Fagaras. The heuristic
suggests that Neamt be expanded first,
because it is closest to Fagaras, but this is
a dead end. The solution is to go first to
vaslui- a step that is actually farther from
the goal according to the heuristis

15. Properties of greedy best-firstProperties of greedy best-first
searchsearch
 Greedy Best first search resembles depth first search in
the way it prefers to follow a single path all the way to
the goal, but will back up when it hits a dead end.
 Complete? No – can get stuck in loops, e.g., Iasi 
Neamt  Iasi  Neamt 
 Time? O(bm
), but a good heuristic can give dramatic
improvement
 Space? O(bm
) -- keeps all nodes in memory
 Optimal? No

16. AA**
searchsearch
Idea: avoid expanding paths that are
already expensive
Evaluation function f(n) = g(n) + h(n)
g(n) = cost so far to reach n
h(n) = estimated cost from n to goal
f(n) = estimated total cost of path
through n to goal

17. AA**
search examplesearch example

18. AA**
search examplesearch example

19. AA**
search examplesearch example

20. AA**
search examplesearch example

21. AA**
search examplesearch example

22. AA**
search examplesearch example

23. Admissible heuristicsAdmissible heuristics
 A heuristic h(n) is admissible if for every node n,
h(n) ≤ h*
(n), where h*
(n) is the true cost to reach the
goal state from n.
 An admissible heuristic never overestimates the cost to
reach the goal, i.e., it is optimistic
 Example: hSLD(n) (never overestimates the actual road
distance)
 Theorem: If h(n) is admissible, A*
using TREE-SEARCH
is optimal




24. Properties of A*Properties of A*
Complete? Yes (unless there are infinitely
many nodes with f ≤ f(G) )
Time? Exponential
Space? Keeps all nodes in memory
Optimal? Yes

25. Example:Example: nn-queens-queens
Put n queens on an n × n board with no
two queens on the same row, column, or
diagonal

26. Hill-climbing searchHill-climbing search
Problem: depending on initial state, can
get stuck in local maxima


27. Genetic algorithmsGenetic algorithms
 A successor state is generated by combining two parent
states
 Start with k randomly generated states (population)
 A state is represented as a string over a finite alphabet
(often a string of 0s and 1s)
 Evaluation function (fitness function). Higher values for
better states.
 Produce the next generation of states by selection,
crossover, and mutation

28. ExampleExample
 Example: 8 queens problem.
A state could be represented as 8 digits each in the range from 1 to
8
Each state is rated by the evaluation function or fitness function. A
Fitness function returns higher values for better states.
Suppose for 8 queens problem fitness function will be based on the
number of non attacking pairs of queens. Suppose fitness value 28
provides a solution.
In the example, the values of 4 states are 24,23, 20 and 11 and for
this variant of genetic algorithm the probability of being chosen a
state for reproducing is directly proportional to be fitness score.
The next steps are selection of parents for reproducing, crossover
and mutation.

29. Crossover point is randomly selected
from the positions in the string.
Lastly, each location is subject to random
mutation with a small independent
probability

30. Genetic algorithmsGenetic algorithms

31. Genetic algorithmsGenetic algorithms
 Fitness function: number of non-attacking pairs of
queens (suppose 28 for a solution)
 24/(24+23+20+11) = 31%
 23/(24+23+20+11) = 29% etc