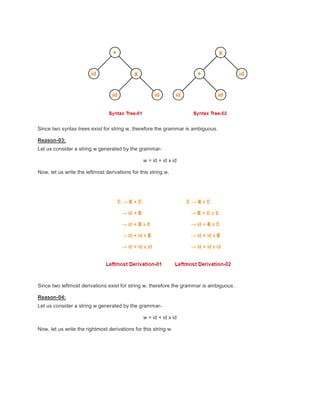
1. A parse tree shows how the start symbol of a grammar derives a string in the language by using interior nodes labeled with nonterminals and children labeled with terminals or nonterminals according to the grammar's productions. 2. An ambiguous grammar is one where a single string can have more than one parse tree, leftmost derivation, rightmost derivation, or other derivation according to the grammar. 3. Operator precedence and associativity determine the order of operations when multiple operators are present in an expression. For example, multiplication generally has higher precedence than addition, and most operators associate left-to-right.

1. Parse Trees
A parse tree pictorially shows how the start symbol of a grammar derives a string in the language. If
nonterminal A has a production A → XYZ, then a parse tree may have an interior node labeled A with three
children labeled X, Y, and Z, from left to right:
Formally, given a context-free grammar, a parse tree according to the grammar is a tree with the following
properties:
1. The root is labeled by the start symbol.
2. Each leaf is labeled by a terminal or by ∊.
3. Each interior node is labeled by a nonterminal.
4. If A is the nonterminal labeling some interior node and X1, X2, . . . , Xn are the labels of the children of
that node from left to right, then there must be a production A → X1 X2 . . Xn. Here, X1, X2, . . . , Xn each
stand for a symbol that is either a terminal or a nonterminal. As a special case, if A → ∊ is a production,
then a node labeled A may have a single child labeled ∊.
Construct parse tree for E --> E + E I E * E I id
Construct parse tree for s --> SS* I ss+ I a

2. Ambiguity
A grammar is said to ambiguous if for any string generated by it, it produces more than one-
 Parse tree
 Or derivation tree
 Or syntax tree
 Or leftmost derivation
 Or rightmost derivation
Consider the following grammar-
E → E + E / E x E / id
This grammar is an example of ambiguous grammar.
Any of the following reasons can be stated to prove the grammar ambiguous-
Reason-01:
Let us consider a string w generated by the grammar-
w = id + id x id
Now, let us draw the parse trees for this string w.
Since two parse trees exist for string w, therefore the grammar is ambiguous.
Reason-02:
Let us consider a string w generated by the grammar-
w = id + id x id
Now, let us draw the syntax trees for this string w.

3. Since two syntax trees exist for string w, therefore the grammar is ambiguous.
Reason-03:
Let us consider a string w generated by the grammar-
w = id + id x id
Now, let us write the leftmost derivations for this string w.
Since two leftmost derivations exist for string w, therefore the grammar is ambiguous.
Reason-04:
Let us consider a string w generated by the grammar-
w = id + id x id
Now, let us write the rightmost derivations for this string w.

4. Syntax Tree Vs Parse Tree

5. Associativity of Operators
When an operand has operators to its left and right, conventions are needed for deciding which operator
applies to that operand. We say that the operator + associates to the left, because an operand with plus
signs on both sides of it belongs to the operator to its left. In most programming languages the four
arithmetic operators, addition, subtraction, multiplication, and division are left-associative. By convention,
9+5+2 is equivalent to (9+5)+2 and 9-5-2 is equivalent to (9-5)-2.
Some common operators such as exponentiation are right-associative. As another example, the
assignment operator = in C and its descendants is right associative; that is, the expression a=b=c is treated
in the same way as the expression a= (b=c).
Operator precedence determines which operator is performed first in an expression with more than one
operators with different precedence. Consider the expression 9+5*2. There are two possible interpretations
of this expression: (9+5) *2 or 9+ (5*2).
The expressions are equivalent to 9+ (5*2) and (9*5) +2, respectively.
Postfix Notation
The examples in this section deal with translation into postfix notation. The postfix notation for an expression
E can be defined inductively as follows:
1. If E is a variable or constant, then the postfix notation for E is E itself.
2. If E is an expression of the form E1
” op E2
”, where op is any binary operator, then the postfix notation for
E is E1
” E2
” op, where E1
” and E2
” are the postfix notations for E1 and E2, respectively.
3. If E is a parenthesized expression of the form (E1), then the postfix notation for E is the same as the
postfix notation for E1.
Example: The postfix notation for (9-5)+2 is 95-2+. That is, the translations of 9, 5, and 2 are the constants
themselves, by rule (1). Then, the translation of 9-5 is 95- by rule (2). The translation of (9-5) is the same
by rule (3). Having translated the parenthesized subexpression, we may apply rule (2) to the entire
expression, with (9-5) in the role of E1 and 2 in the role of E2, to get the result 95-2+. As another example,
the postfix notation for 9- (5+2) is 952+-. That is, 5+2 is first translated into 52+, and this expression
becomes the second argument of the minus sign.