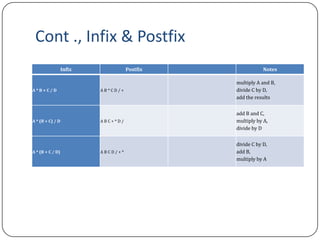
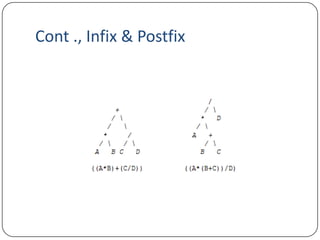
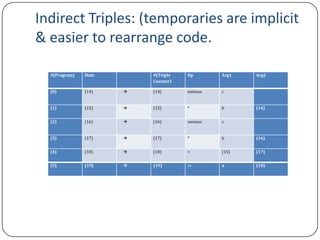
The document discusses various topics related to compiler design including ambiguous grammar, leftmost and rightmost derivations, infix and postfix notation, and implementations of three-address code. It provides examples of ambiguous grammar in C and describes leftmost and rightmost derivations in parsing. It also compares infix, postfix and prefix notation for mathematical expressions and describes converting between the notations. Finally, it discusses different implementations of three-address code including using quadruples, triples and indirect triples.

1. Ambiguous grammar, LMD & RMD, Infix &
Postfix, Implementation Of 3 address Code
Compiler Design

2. Team Members
Group-I Assignment Topic : BRESENHARAM'S ALGORITHM (ELIPSE Drawing)
Group's representative: TANGUTURU SAI KRISHNA
S.No. BITS ID NAME Official Email ID Personal Email ID
1 2011HW69898
TANGUTURU SAI KRISHNA saikrishna.tanguturu@wipro.com sai.tsk2008@gmail.com
2 2011HW69900
RAYAPU MOSES rayapu.moses@wipro.com stalinkvd001@gmail.com
3 2011HW69932 SHENBAGAMOORTHY A
shenbagamoorthy.a83@wipro.com moorthy2626@gmail.com
4 2011HW69913
ANURUPA K C anurupa.c85@wipro.com anu.rupa30@gmail.com
5 2011HW69909
ARUNJUNAISELVAM P arunjunaiselvam.p95@wipro.com arunjunai.carrer@gmail.com
6 2011HW69569
PRANOB JYOTI KALITA pranob.kalita@wipro.com pranob.kalita90@gmail.com
7 2011HW69893
TINNALURI V N PRASANTH prasanth.tinnaluri@wipro.com naga.prasanth985@gmail.com
8 2011HW69904
KONDALA SUMATHI sumathi.kondala@wipro.com sumathi.kondala@gmail.com
9 2011HW69896
DASIKA KRISHNA dasika.krishna@wipro.com dasikakrishnas@gmail.com
10 2011HW69907
SHEIK SANAVULLA sheik.sanavulla@wipro.com sanavulla.sms@gmail.com

3. What is an ambiguous grammar? Give
an example.
 In computer science, a context-free grammar is said to be an ambiguous grammar if
there exists a string which can be generated by the grammar in more than one way
(i.e., the string admits more than one parse tree or, equivalently, more than one
leftmost derivation). A context-free language is inherently ambiguous if all context-
free grammars generating that language are ambiguous.
Some programming languages have ambiguous grammars; in this case, semantic
information is needed to select the intended parse tree of an ambiguous construct.
For example, in C the following:
x * y ;
can be interpreted as either:
* the declaration of an identifier named y of type pointer-to-x, or
* an expression in which x is multiplied by y and then the result is discarded.
To correctly choose between the two possible interpretations, a compiler must
consult its symbol table to find out whether x has been declared as a typedef name
that is visible at this point.

4. Leftmost and Rightmost Derivations
 At any stage during a parse, when we have derived some sentential form
(that is not yet a sentence) we will potentially have two choices to make:
 which non-terminal in the sentential form to apply a production rule to
 which production rule for that non-terminal to apply
 Eg. in the above example, when we derived , we could then have applied a
production rule to any of these three non-terminals, and would then have
had to choose among all the production rules for either or .
 The first decision here is relatively easy to solve: we will be reading the
input string from left to right, so it is our own interest to derive the
leftmost terminal of the resulting sentence as soon as possible. Thus, in a
top-down parse we always choose the leftmost non-terminal in a sentential
form to apply a production rule to - this is called a leftmost derivation.
 If we were doing a bottom-up parse then the situation would be reversed,
and we would want to do apply the production rules in reverse to the
leftmost symbols; thus we are performing a rightmost derivation in
reverse.

5. Cont., Leftmost Derivations

6. Cont., Rightmost Derivations

7. Infix & Postfix
 Infix, Postfix and Prefix notations are three different but equivalent ways of writing expressions. It is
easiest to demonstrate the differences by looking at examples of operators that take two operands.
 Infix notation: X + Y
 Operators are written in-between their operands. This is the usual way we write expressions. An
expression such as A * ( B + C ) / D is usually taken to mean something like: "First add B and C
together, then multiply the result by A, then divide by D to give the final answer."
 Infix notation needs extra information to make the order of evaluation of the operators clear: rules built
into the language about operator precedence and associativity, and brackets ( ) to allow users to
override these rules. For example, the usual rules for associativity say that we perform operations from
left to right, so the multiplication by A is assumed to come before the division by D. Similarly, the usual
rules for precedence say that we perform multiplication and division before we perform addition and
subtraction
 Postfix notation (also known as "Reverse Polish notation"): X Y +
 Operators are written after their operands. The infix expression given above is equivalent to
A B C + * D /
The order of evaluation of operators is always left-to-right, and brackets cannot be used to change this
order. Because the "+" is to the left of the "*" in the example above, the addition must be performed
before the multiplication.
Operators act on values immediately to the left of them. For example, the "+" above uses the "B" and "C".
We can add (totally unnecessary) brackets to make this explicit:
( (A (B C +) *) D /)
Thus, the "*" uses the two values immediately preceding: "A", and the result of the addition. Similarly, the
"/" uses the result of the multiplication and the "D".

8. Cont ., Infix & Postfix
Infix Postfix Notes
A * B + C / D A B * C D / +
multiply A and B,
divide C by D,
add the results
A * (B + C) / D A B C + * D /
add B and C,
multiply by A,
divide by D
A * (B + C / D) A B C D / + *
divide C by D,
add B,
multiply by A

9. Cont ., Infix & Postfix
 Converting between these notations
 The most straightforward method is to start by
inserting all the implicit brackets that show the
order of evaluation e.g.:
 Infix Postfix
( (A * B) + (C / D) ) ( (A B *) (C D /) +)
((A * (B + C) ) / D) ( (A (B C +) *) D /)
(A * (B + (C / D) ) ) (A (B (C D /) +) *)

10. Cont ., Infix & Postfix
 You can convert directly between these bracketed
forms simply by moving the operator within the
brackets e.g. (X + Y) or (X Y +) or (+ X Y). Repeat this
for all the operators in an expression, and finally
remove any superfluous brackets.
 You can use a similar trick to convert to and from
parse trees - each bracketed triplet of an operator
and its two operands (or sub-expressions)
corresponds to a node of the tree. The
corresponding parse trees are:

11. Cont ., Infix & Postfix

12. Implementation Of 3 address Code:
 A three-address statement is an abstract form of
intermediate code. In a compiler, these statements
can be implemented as records with fields for the
operator and the operands. Three such
representations are quadruples, triples, and
indirect triples.
 There are 3 methods in which 3 address code.
1. Quadrupules,
2. Triples,
3. Indirect Triples

13. Quadrupules,Triples & Indirect Triples
 Quadruples
 A quadruple is a record structure with four fields, which we
call op, arg l, arg 2, and result. The op field contains an
internal code for the operator. The three-address statement
x:= y op z is represented by placing y in arg 1. z in arg 2. and x
in result. Statements with unary operators like x: = – y or x: =
y do not use arg 2. Operators like param use neither arg2 nor
result. Conditional and unconditional jumps put the target
label in result. The quadruples in Fig. H.S(a) are for the
assignment a: = b+ – c + b i – c. They are obtained from the
three-address code in Fig. 8.5(a). The contents of fields arg 1,
arg 2, and result are normally pointers to the symbol-table
entries for the names represented by these fields. If so,
temporary names must be entered into the symbol table as
they are created.
 Eg. a := b * -c + b * -c

14. Quadruples:(easy to rearrange code for
global optimization, lots of temporaries)
Quadruples:(easy to rearrange code for global optimization, lots of temporaries)
# Op Arg1 Arg2 Res
(0) uminus c t1
(1) * b t1 t2
(2) uminus c t3
(3) * b t3 t4
(4) + t2 t4 t5
(5) := t5 a

15.  Triples
 To avoid entering temporary names into the symbol
table. we might refer to a temporary value bi the
position of the statement that computes it. If we do so,
three-address statements can be represented by records
with only three fields: op, arg 1 and arg2, as in Fig.
8.8(b). The fields arg l and arg2, for the arguments of op,
are either pointers to the symbol table (for
programmer- defined names or constants) or pointers
into the triple structure (for temporary values). Since
three fields are used, this intermediate code format is
known as triples.’ Except for the treatment of
programmer-defined names, triples correspond to the
representation of a syntax tree or dag by an array of
nodes, as below

16. Triples: (temporaries are implicit,
difficult to rearrange code)
# Op Arg1 Arg2
(0) uminus c
(1) * b (0)
(2) uminus c
(3) * b (2)
(4) + (1) (3)
(5) := a (4)

17.  Indirect Triples
 Another implementation of three-address code that
has been considered is that of listing pointers to
triples, rather than listing the triples themselves.
This implementation is naturally called indirect
triples. For example, let us use an
array statement to list pointers to triples in the
desired order.

18. Indirect Triples: (temporaries are implicit
& easier to rearrange code.
#(Program) Stmt #(Triple
Counter)
Op Arg1 Arg2
(0) (14)  (14) uminus c
(1) (15)  (15) * b (14)
(2) (16)  (16) uminus c
(3) (17)  (17) * b (16)
(4) (18)  (18) + (15) (17)
(5) (19)  (19) := a (18)

19. Thank You