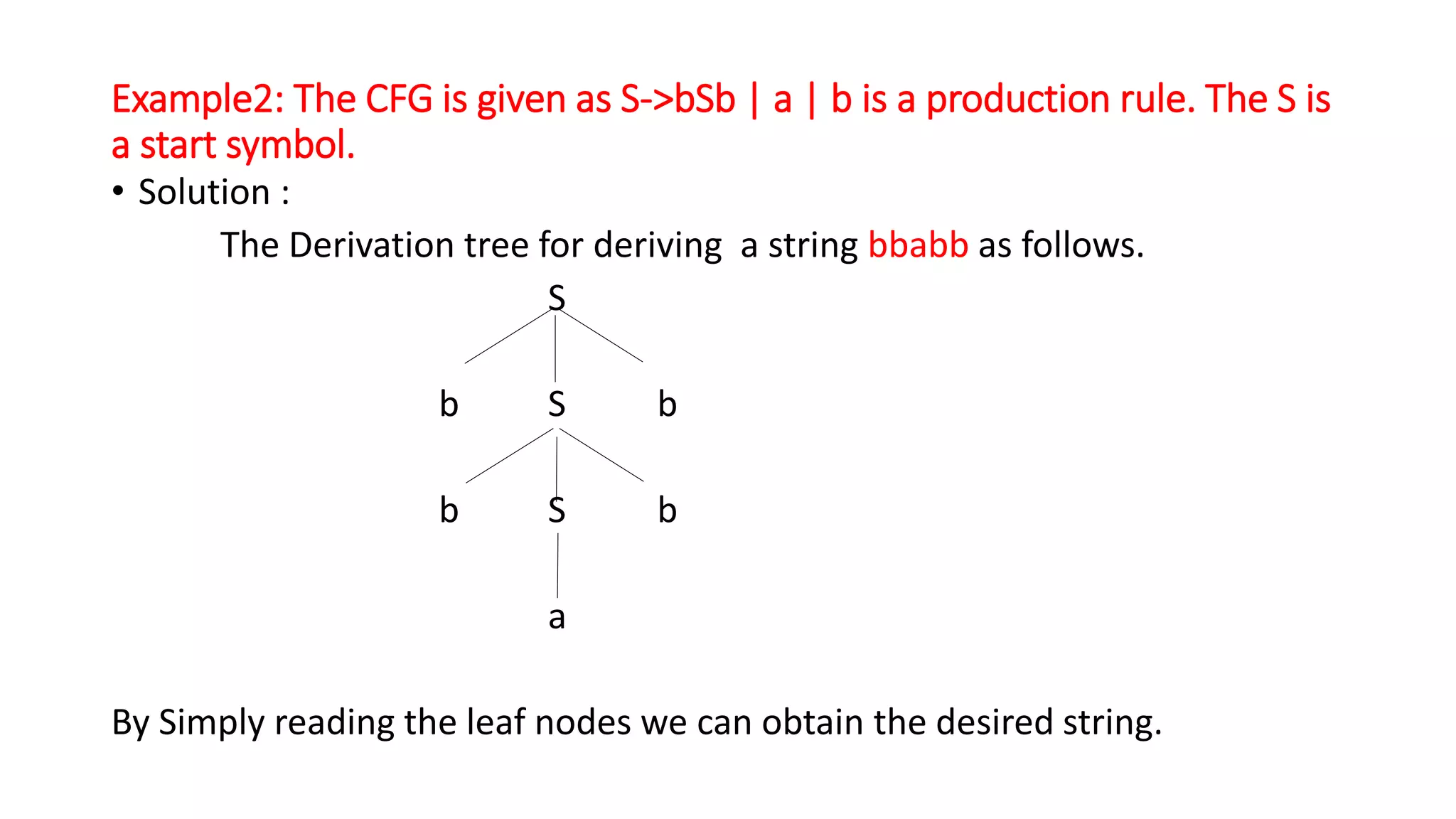
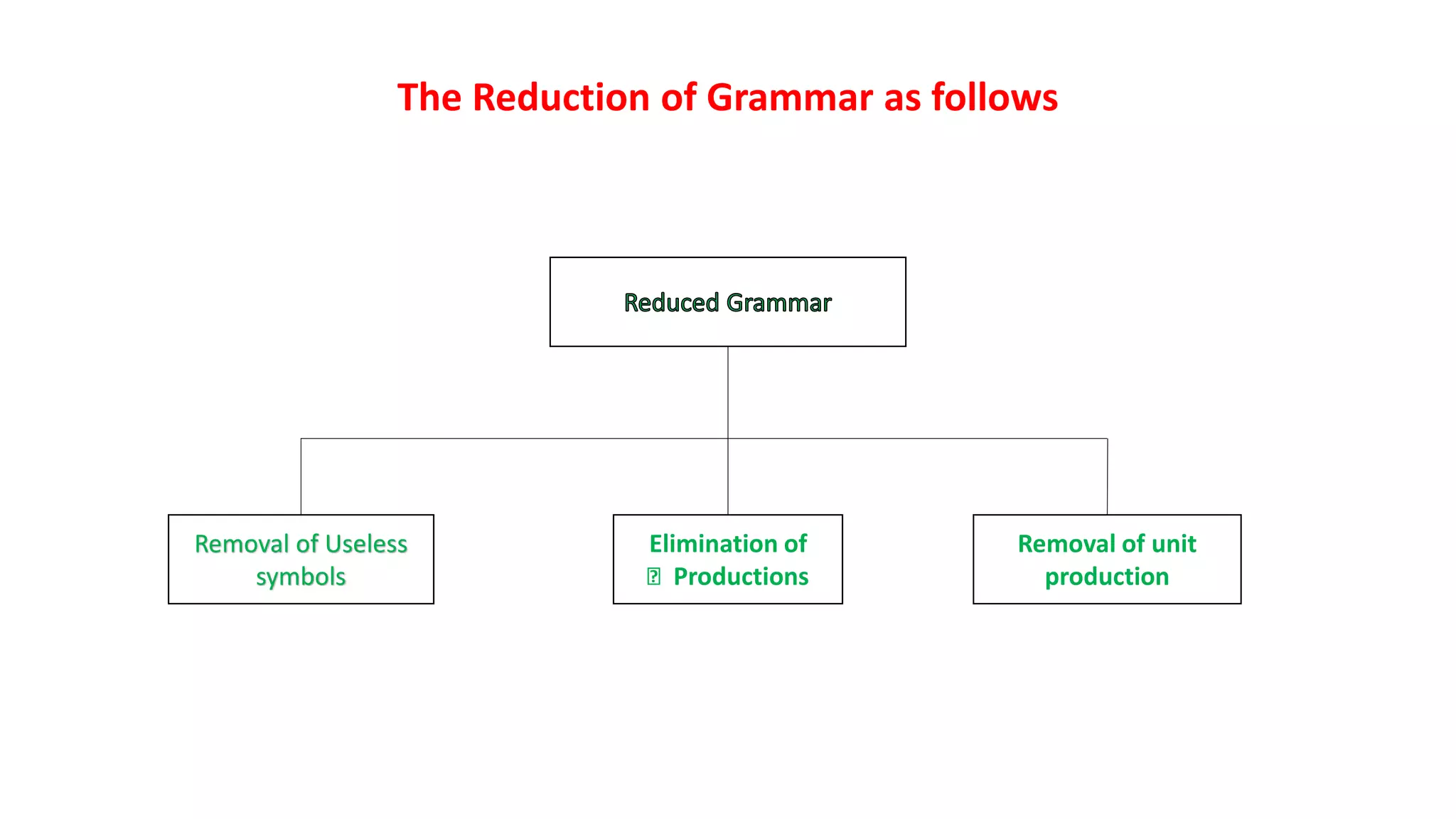
The document provides information about context free grammar (CFG). It defines a CFG as G=(V,T,P,S) where V is the set of nonterminals, T is the set of terminals, P is the set of production rules, and S is the start symbol. Examples of CFGs are provided. Derivation trees, which show the derivation of strings from a CFG, are also discussed. The key differences between regular grammars and CFGs are summarized. Methods for minimizing CFGs by removing useless symbols, epsilon productions, and unit productions are outlined.

1. CONTEXT FREE
GRAMMAR
M RATNAKAR BABU
Asst.Prof. CSE

2. Prerequisite
1. At very first session we have seen that the Finite Automata and
importance of Finite State Machines and the construction of
Deterministic Finite Automata and some examples on it.
2. In previous session we have seen that the construction of Regular
Expressions for the given problems and how to generate a Regular
expression from the DFA and vice versa.
3. The above two concepts are required to understand the Context
Free Grammar and the applications of CFG.

3. DEFINITION
• The Context Free Grammar can be defined as a set denoted by G=(V,T,P,S)
Where
V- set of non-terminals Ex: { P,Q,R…}
T- set of Terminals Ex: {p,q,r …}
P- set of Production rules
Where non-terminal -> non-terminal
non-terminal -> terminal
S- is start symbol.

4. EXAMPLE
• G=({S},{0,1},P,S)
Where P = { S->0S
S->1S
S->Ꜫ }

5. Example1 : Construct CFG which consists of all the strings having atleast one
occurrence of ‘000’ over input {0,1}.
• Solution:
We need to construct the equivalent R.E for the given problem
first.
The R.E=(any number of 0’s or 1’s) 000 (any number of 0’s or 1’s)
Thus R.E = (0+1)*000(0+1)*
Now let us build the production rules to satisfy the above R.E
{ S->ATA
A->0A|1A|Ꜫ
T->000 }

6. Excercise1: Find the CFG for the odd length of strings in{a,b}*
with middle symbol a
Excercise2: Generate the a CFG to obtain balanced set of
parenthesis(i.e. every left parenthesis should match with
corresponding right parenthesis)

7. Derivation Trees
• Definition: Derivation tree is a graphical representation for the
derivation of the given production rules for a given CFG.
• It is the simple way to show how the derivation can be done to obtain
some string from given set of production rules.
• The derivation tree is also called as Parse tree.
Properties of Derivation Tree:-
1. The root node is always a node indicating start symbol.
2. The derivation is read from left to right.
3. The leaf nodes are always terminal nodes.
4. The interior nodes are always the non-terminal nodes.

8. Example2: The CFG is given as S->bSb | a | b is a production rule. The S is
a start symbol.
• Solution :
The Derivation tree for deriving a string bbabb as follows.
S
b S b
b S b
a
By Simply reading the leaf nodes we can obtain the desired string.

9. Exercise : Construct the derivation tree for the string ‘aabbabba’ from
the CFG given by
S->aB|bA
A->a|aS|bAA
B->b|bS|aBB

10. Difference between Regular Grammar and Context Free Grammar
S.No. REGULAR GRAMMAR CONTEXT FREE GRAMMAR
1 Regular grammar is Defined as G=(V,T,P,S)
where V- set of Non-Terminals,
T- set of Terminals, P- set of Production rules, S-
start Symbol
Hence G be a regular Grammar.
The Context free grammar is defined as follows G=(V,T,P,S)
where V- set of Non-Terminals,
T- set of Terminals, P- set of Production rules, S- start Symbol
Hence G be a CFG.
2 Using this grammar we can draw DFA Using this we can construct Push Down Automata(PDA)
3 Compiler can not make use of this for Parsing. Compiler makes use of this for Parsing.
4 The grammar accepts small set of languages.
Hence it is type-3 grammar.
The grammar accepts a large set of languages. Hence it is
type-2 grammar.
5 This form of grammar can be represented by left
linear or right linear grammar
This form of grammar can be represented as nonterminal->
set of terminals and non terminals.
6 Every regular grammar is context free grammar. Every Context Free Grammar can not be Regular
7 For Ex: S->aA|B
A->aA|a
B->bB|b
For Example:
S->aSb|bSb|Ꜫ
8 Syntax of any programming language can not be
represented completely by regular grammar
Syntax of any programming language can be represented
completely by regular grammar

11. MINIMIZATION OF CFG
• The properties of reduced grammar are as follows.
1. Each variable(i.e. non terminal) and each terminal of G appears in the
derivation of some word in L.
2. There should not be any production as X->Y where X and Y are non
terminal.
3. If Ꜫ is not in the language L then there need not be the production X-> Ꜫ.

12. The Reduction of Grammar as follows
Removal of Useless
symbols
Elimination of
Ꜫ Productions
Removal of unit
production

13. Removal of useless symbols
• Any symbol is not useful when it appears on R.H.S. in the production rule. If no
such derivation exists then it is supposed to be a useless symbol.
For Example:
G= (V,T,P,S) where V={S,T,X} T={0,1}
S->0T|1T|X|0|1
T->00
In the above grammar S->X there is no further rule as a definition to X. Hence we
can declare X is a useless symbol. Therefore we can remove the S-> X production
from the given grammar.
After removal of useless symbol form the given grammar the Grammar should be
as follows.
G= (V,T,P,S) where V={S,T} T={0,1}
S->0T|1T|0|1
T->00

14. Excercise1: Eliminate the useless symbols from the following grammar
S->aS|A|C
A->a
B->aa
C->aCb
Exercise 2: Eliminate the useless symbols from the given grammar.
S->aA|a|Bb|cC
A->aB
B->a|Aa
C->cCD
D->ddd

15. Elimination of Ꜫ production
• In CFG if there is Ꜫ production we can remove it ,without changing the
meaning of the grammar.
Example:
S->0S|1S| Ꜫ
from the above Grammar we can remove Ꜫ production without
changing the meaning of it.
Simply if we place S-> Ꜫ in other rules.
we get S->0 and S->1 Hence we can rewrite the productions as
follows
S->0S|1S|0|1
Thus we can remove Ꜫ production from the given grammar

16. Example2: For the CFG given below remove Ꜫ production
S->aSa
S->bSb
S-> Ꜫ
• Solution:
According to the replacement procedure we will place Ꜫ at S in
the sentential form.
S->aSa if S= Ꜫ
S->aa
Similarly if
S->bSb if S= Ꜫ
S->bb
Thus finally rules are
S->aSa|bSb|aa|bb
Thus we can remove Ꜫ production from the given grammar.

17. Excercise1: Eliminate Ꜫ productions from the CFG given below
A->0B1|1B1
B->0B|1B|Ꜫ
Exercise 2: Construct the CFG without Ꜫ productions form the given
Grammar.
S->a|Ab|aBa
A->b|Ꜫ
B->b|A

18. Removal of Unit Productions
• The unit productions are the productions in which one non terminal
gives another non terminal.
For example X->Y, Y->Z, Z->X are the unit productions.
Example 1: if CFG is as below
S->0A|1B|C
A->0S|00
B->1|A
C->01 then remove the unit productions.
Solution:
Clearly S->C is a unit production. But while removing it we have
to consider what C gives. So, we add a rule to S.
S->0A|1B|01

19. Example 1(2):
• Similarly B->A is also unit production so we can modify it as
B->1|0S|00
Thus finally we can write CFG without unit productions as
S->0A|1B|01
A->0S|00
B->1|0S|00
C->01

20. Exercise: Eliminate the unit productions fro the Grammar
S->AB
A->a
B->C|b
C->D
D->E|bC
E->d|Ab

21. Next Class:
•We will discuss about the Push Down Automata.
•Conversion of CFG to PDA and some exercises.
•Construction of CFG from PDA some exercises.

22. End For Now
Continue in Next Class.

23. Solution:
Back
a or b a or ba
Length n Length n
Thus the R.E = (a+b)n a (a+b)n Where n>=0
As the above given expression doesn’t represent regular language, The DFA can
not be designed for representing such language.
The CFG G= (V,T,P,S)
Where
V={S}
T={a,b}
P={ S->aSa|bSb|aSb|bSa|a}
S is Start Symbol.

24. Solution:
Back
The well formed parenthesis means whenever opening parentheses is
present there should be a closing parentheses associated with it.
Any expression must begin with opening bracket .We will consider
T={(,[,),]} as set of brackets.
The CFG G=(V,T,P,S)
Where V={S}
T={(,[,),]}
P={ S->SS|()|[]|(S)|[S]
Where S is Start Symbol.

25. Solution :
• To draw a tree we will first try to
obtain derivation for the string
aabbabba.
S
aB S->aB
a aBB B->aBB
aa bS B B->bS
aab bA B S->bA
aabba B A->a
aabba bS B->bS
aabbab bA S->bA
aabbabba A->a
• Now let us draw a tree
S
a B
a B B
b S b S
b A b A
a a
Back

26. Solution:
• We will first write all the productions that are giving terminal symbols.
A->a
B->aa
But if we look at start symbol S then
S->aS|A|C
There is no production for B from start symbol. Thus B become a useless
symbol.
Similarly, S->C->aCb->aaCbb->….
There is no terminating symbol for C, Therefore we will eliminate C.
Then the set of rules are
S->aS|A
A->a
Back

27. Solution:
• Consider all the productions that are giving terminal symbols
S->a
B->a
D->ddd
Now Consider
S->cC
C->cCD
D->ddd.
We will try to derive the string using production rule C we get ,
S->cC->ccCddd->cccCDddd->….
We will not get any terminal symbol for C. Thus we can eliminate C production . To reach D , Cis the only
production, As C is eliminated there is no point of D production. Hence , D is also eliminated.
Therefore,
S->aA|a|Bb
A->aB
B->a|Aa
Is the reduced Grammar.
Back

28. Solution:
• Now the Ꜫ production is B->Ꜫ we will delete this production, And then add
the production having B replaced by Ꜫ
A->0B1 if B=Ꜫ
A->01
Similarly, A->1B1->11
A->0B1|1B1|01|11
Similarly,
B->0B->0
B->1B->1
B->0B|1B |0|1
Collectively we can write
A->0B1|1B1|01|11
B->0B|1B|0|1
Back

29. Solution:
• As S->AB and A->a
There is only one rule with A which is giving terminal symbol. Hence there is no Unit production with A.
Now Consider,
B->C
C->D
D->E
It is clear that B,C and D are Unit Productions. As E->d|Ab, we will replace value of D. Then
D->d|Ab|bC
Similarly, a C->D we can write
C->d|Ab|bC
Hence B->d|Ab|bC|b
Thus the grammar after removing unit productions
S->AB
A->a
B->d|Ab|bC|b
C->d|Ab|bC
Back

30. Solution: