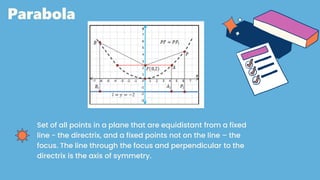
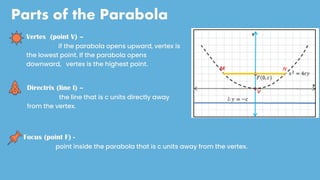
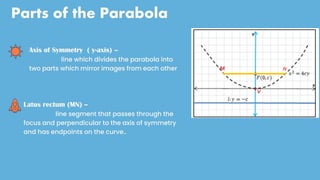
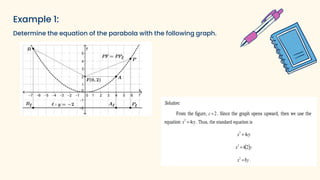
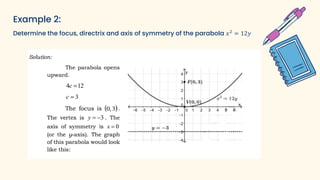
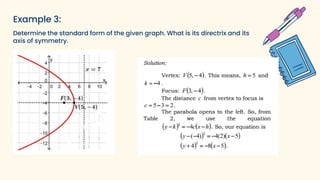
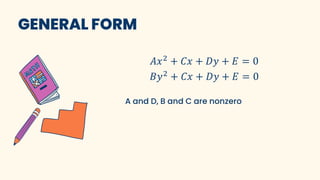
The document discusses parabolas and quadratic functions. It defines a parabola as the set of all points equidistant from a fixed line (the directrix) and a fixed point (the focus). It explains that the graph of a quadratic function f(x)=ax^2+bx+c is a parabola that opens upward if a>0 and downward if a<0. The document also identifies and describes the key parts of a parabola including the vertex, focus, directrix, and axis of symmetry. It provides the standard forms of parabolas with the vertex at the origin or a non-origin point (h,k). Several examples are worked through to identify the standard form,

1. PARABOLA

2. Quadratic
Function
𝑓 𝑥 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐
𝑓 𝑥 = 𝑎(𝑥 − ℎ)2
Their graph is called parabola that
opens upward or downward.
How to determine if the graph opens
downward or upward?
Consider the sign of the leading
coefficient a of the quadratic function.
if a is positive, it opens upward.
If a is negative, it opens downward.

3. Example:
Identify if it open upward or downward.
1. 𝑓 𝑥 = −𝑥2
+ 8𝑥 − 15
2. 𝑓 𝑥 = (𝑥 + 6)2
−5
3. 𝑓 𝑥 = 4 + 2𝑥 − 𝑥2
4. 𝑓 𝑥 =
1
2
(𝑥2
− 4𝑥 − 1)

4. Parabola
Set of all points in a plane that are equidistant from a fixed
line - the directrix, and a fixed points not on the line – the
focus. The line through the focus and perpendicular to the
directrix is the axis of symmetry.

5. Parts of the Parabola
Vertex (point V) –
if the parabola opens upward, vertex is
the lowest point. If the parabola opens
downward, vertex is the highest point.
Directrix (line l) –
the line that is c units directly away
from the vertex.
Focus (point F) -
point inside the parabola that is c units away from the vertex.

6. Parts of the Parabola
Axis of Symmetry ( y-axis) –
line which divides the parabola into
two parts which mirror images from each other
Latus rectum (MN) –
line segment that passes through the
focus and perpendicular to the axis of symmetry
and has endpoints on the curve..

7. A. Vertex at the Origin
STANDARD FORM
Equation Focus Directrix
Axis of
Symmetry
Parabola
opens
𝑦2
= 4𝑐𝑥 (c,0) x = -c x - axis to the right
𝑦2
= −4𝑐𝑥 (-c,0) x = c x - axis to the left
𝑥2
= 4𝑐𝑦 (0,c) y = -c y - axis upward
𝑥2
= −4𝑐𝑦 (0,-c) y = c y - axis downward

8. Example 1:
Determine the equation of the parabola with the following graph.

9. Example 2:
Determine the focus, directrix and axis of symmetry of the parabola 𝑥2
= 12𝑦

10. A. Vertex at the (h, k)
STANDARD FORM
Equation Focus Directrix
Axis of
Symmetry
Parabola
opens
(𝑦 − 𝑘)2
= 4𝑐(𝑥 − ℎ) (h + c, k) x = h - c y = k to the right
(𝑦 − 𝑘)2
= −4𝑐(𝑥 − ℎ) (h - c, k) x = h + c y = k to the left
(𝑥 − ℎ)2
= 4𝑐(𝑦 − 𝑘) (h, k + c) y = k - c x = h upward
(𝑥 − ℎ)2
= −4𝑐(𝑦 − 𝑘) (h, k - c) y = k + c x = h downward

11. Example 3:
Determine the standard form of the given graph. What is its directrix and its
axis of symmetry.

12. GENERAL FORM
𝐴𝑥2 + 𝐶𝑥 + 𝐷𝑦 + 𝐸 = 0
𝐵𝑦2
+ 𝐶𝑥 + 𝐷𝑦 + 𝐸 = 0
A and D, B and C are nonzero

13. Example 3:
Rewrite the equation (𝑦 + 4)4
= −8 𝑥 − 5 into its general form.

14. Example 3:
Determine the vertex, focus, directrix, and axis of symmetry of the parabola
𝑦2
− 5𝑥 + 12𝑦 = −16. Sketch the parabola, and include these points and lines.
Solution:

15. Exercises:

16. Exercises:

17. Exercises:

18. Exercises:

20. Thank you!