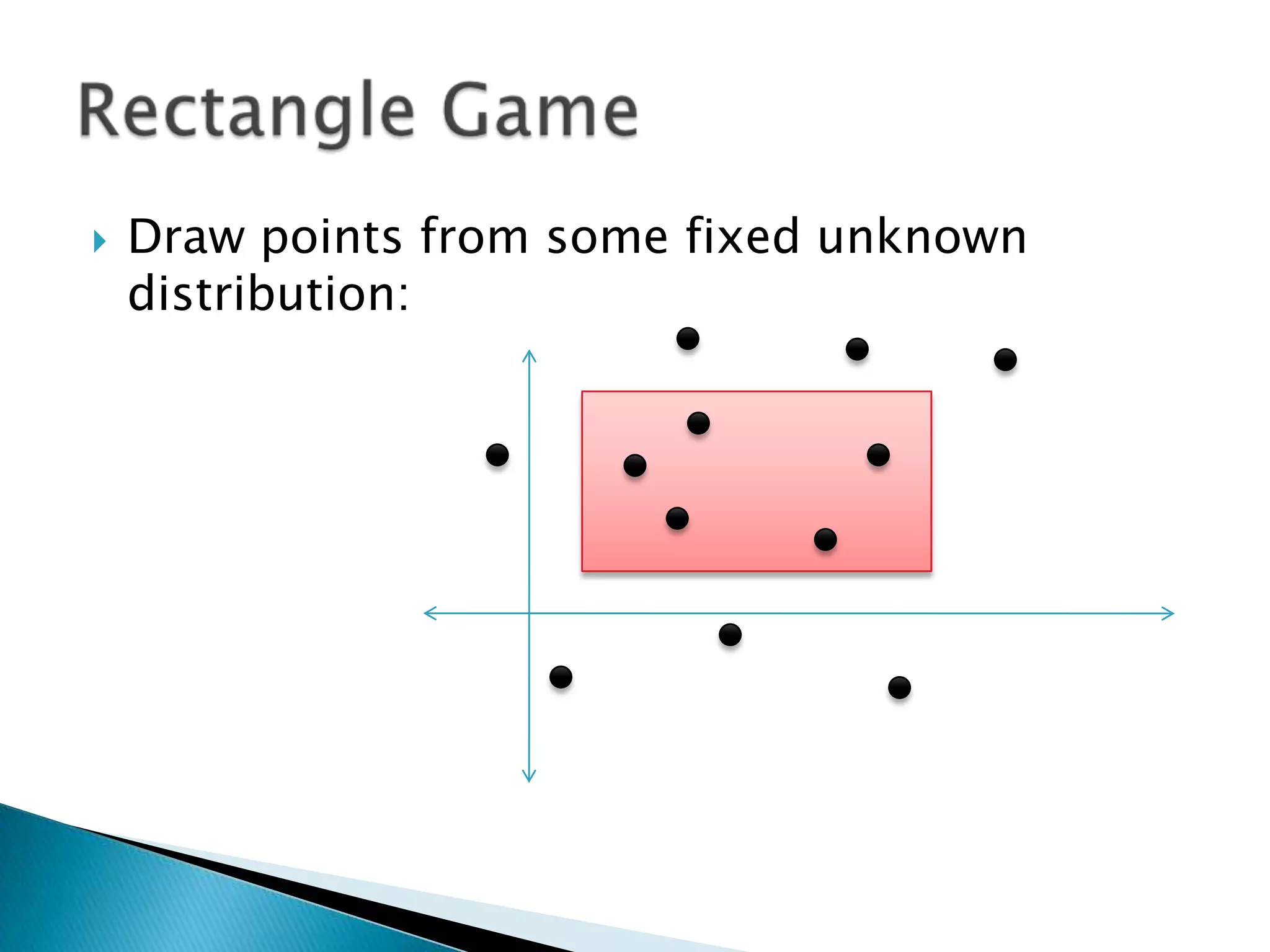
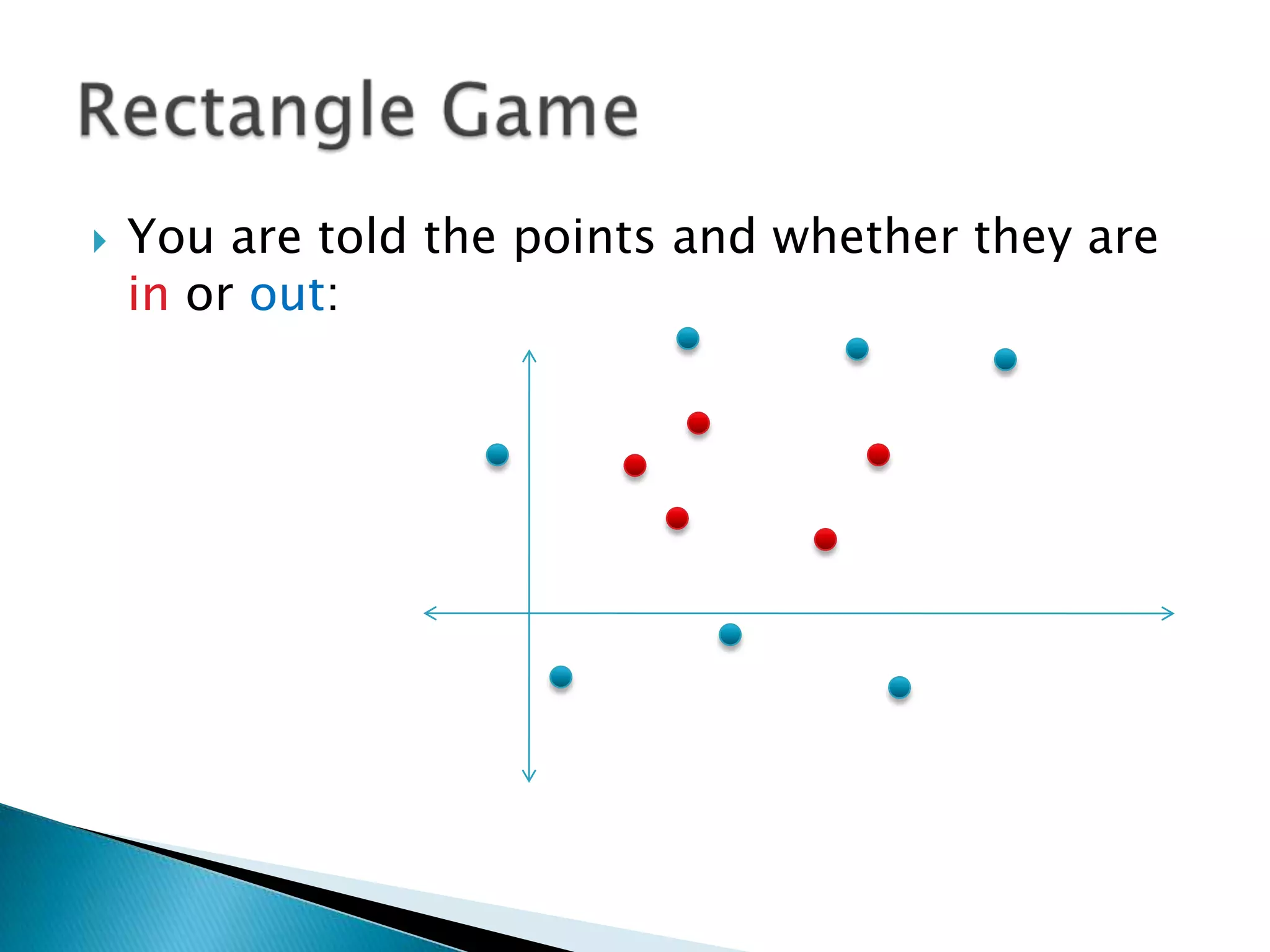
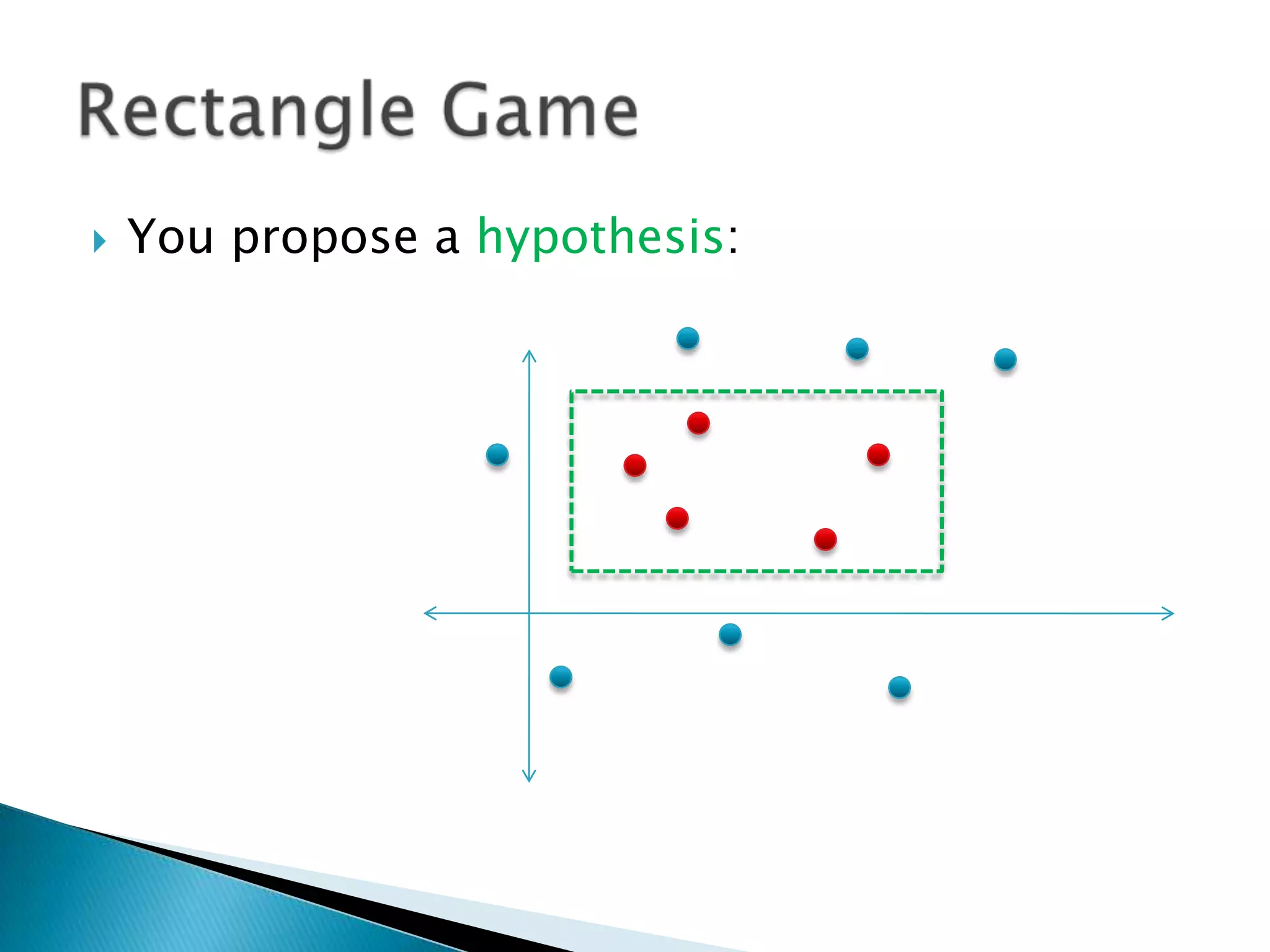
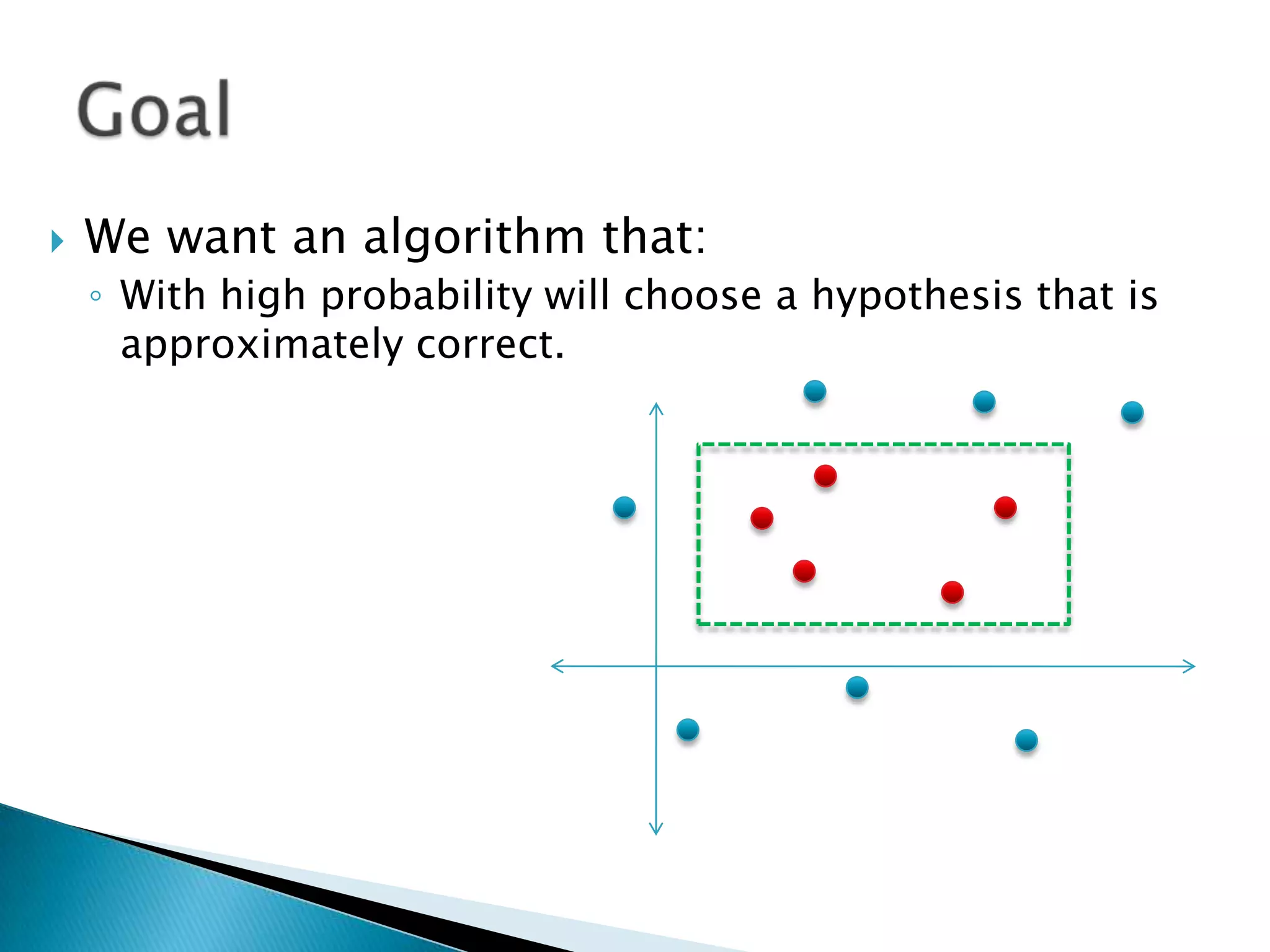
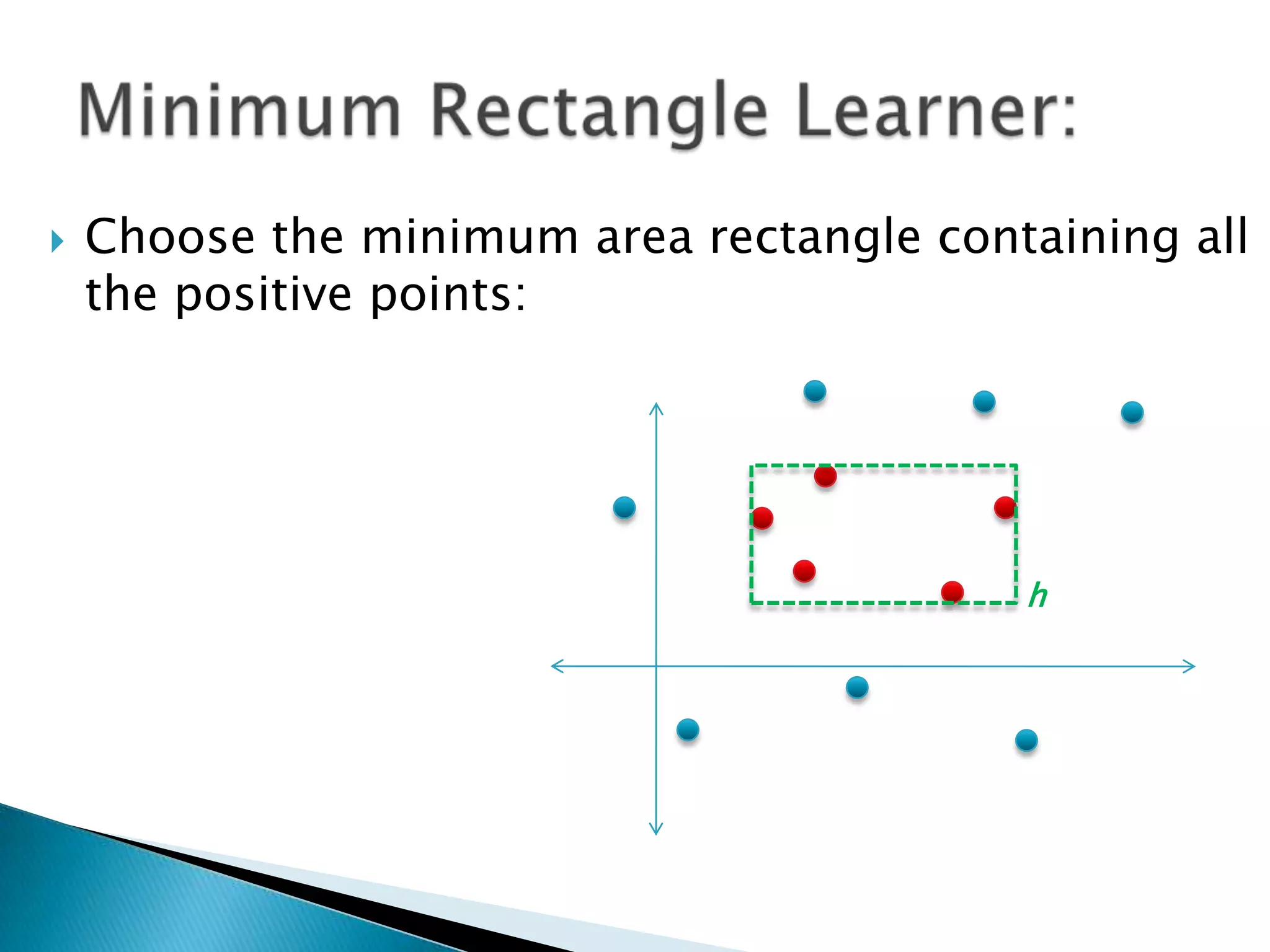
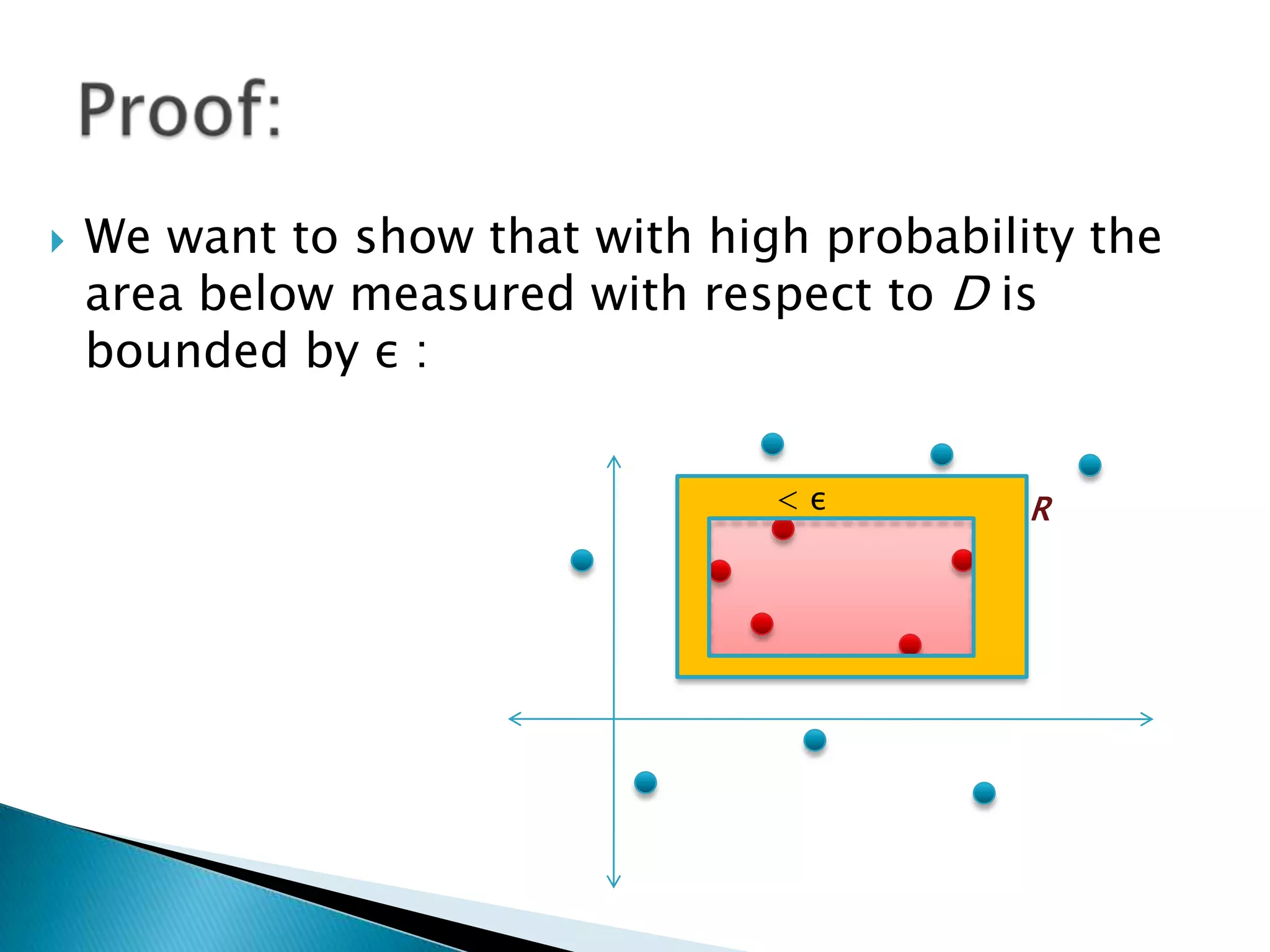
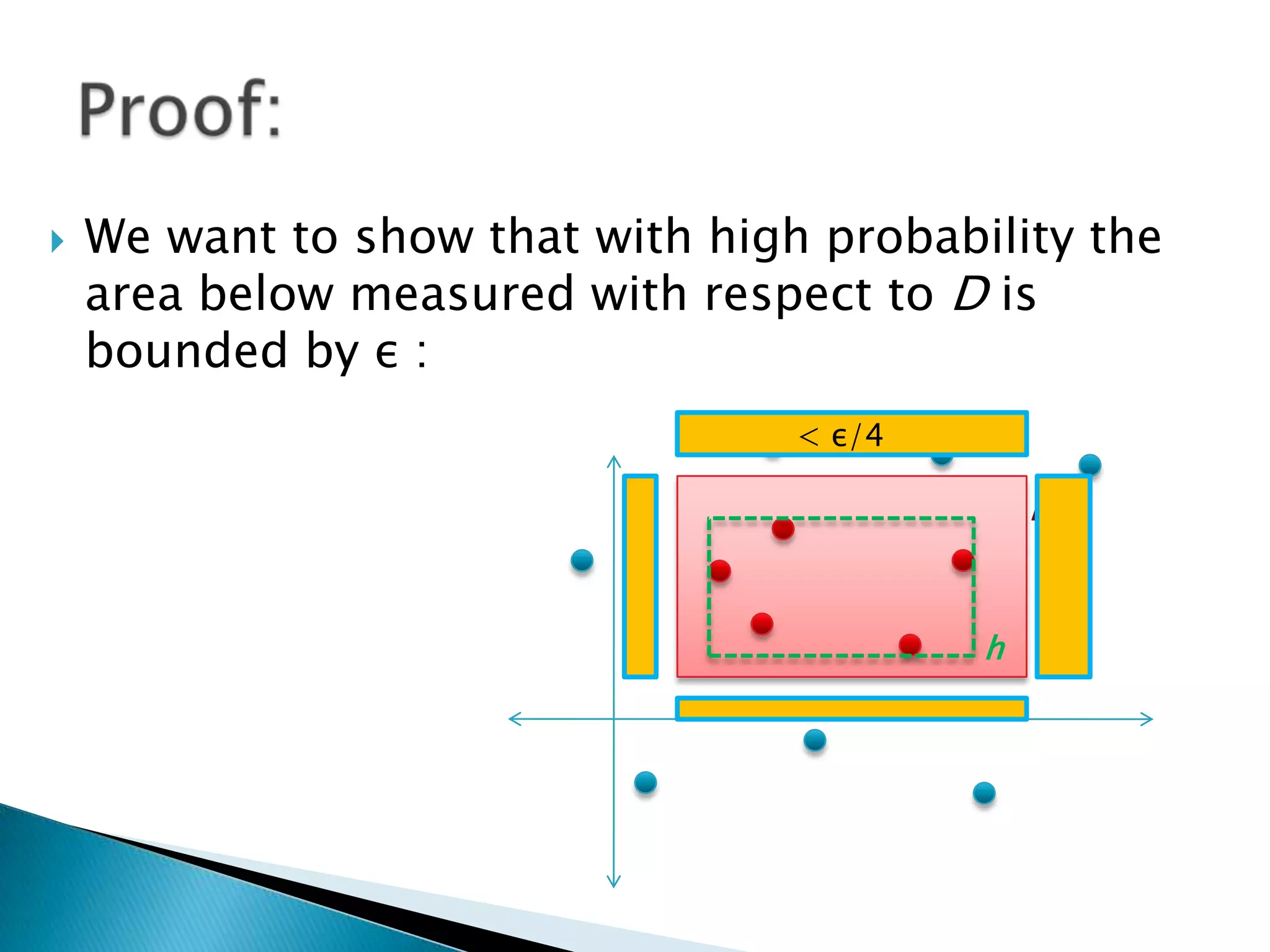
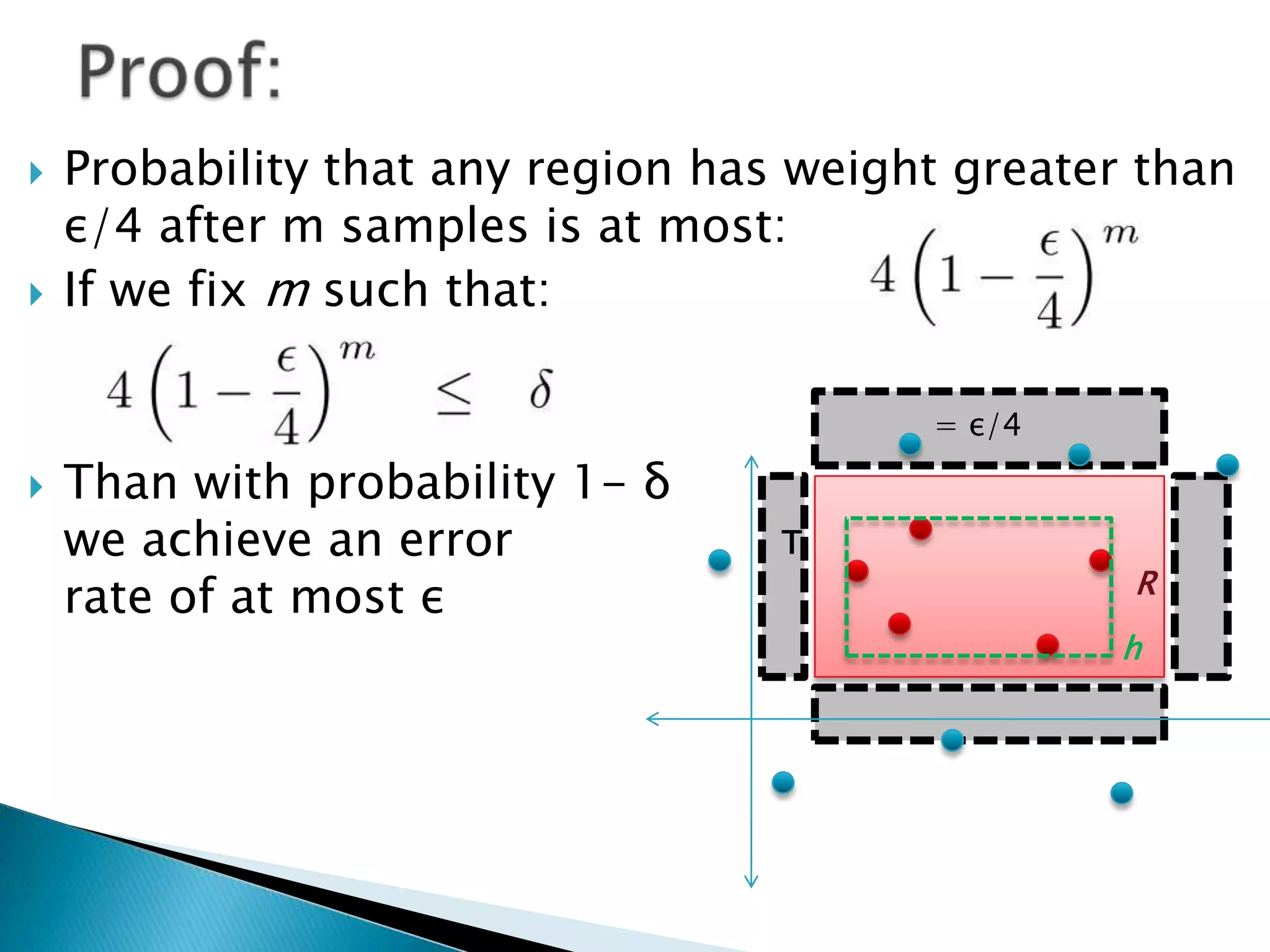
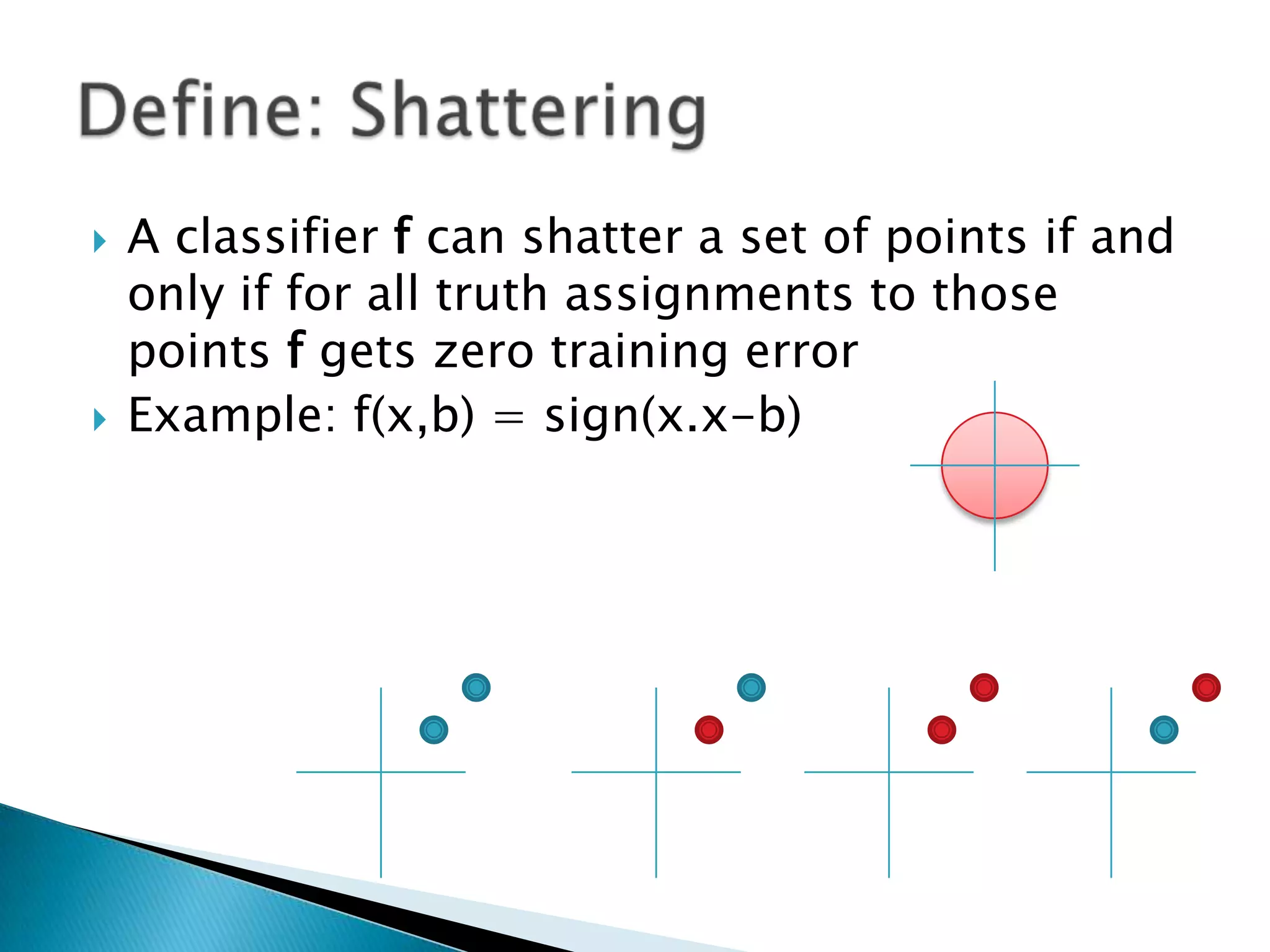
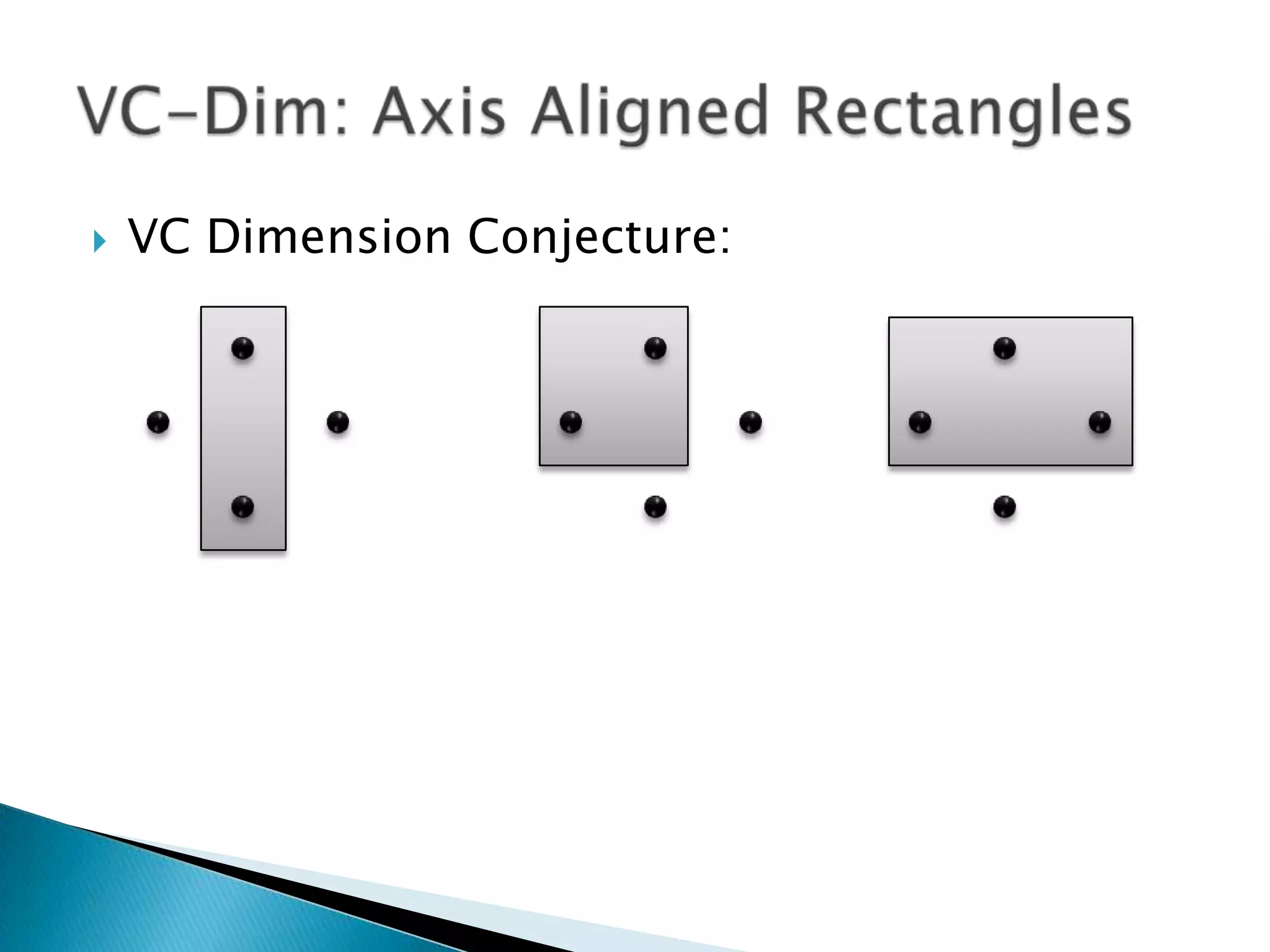
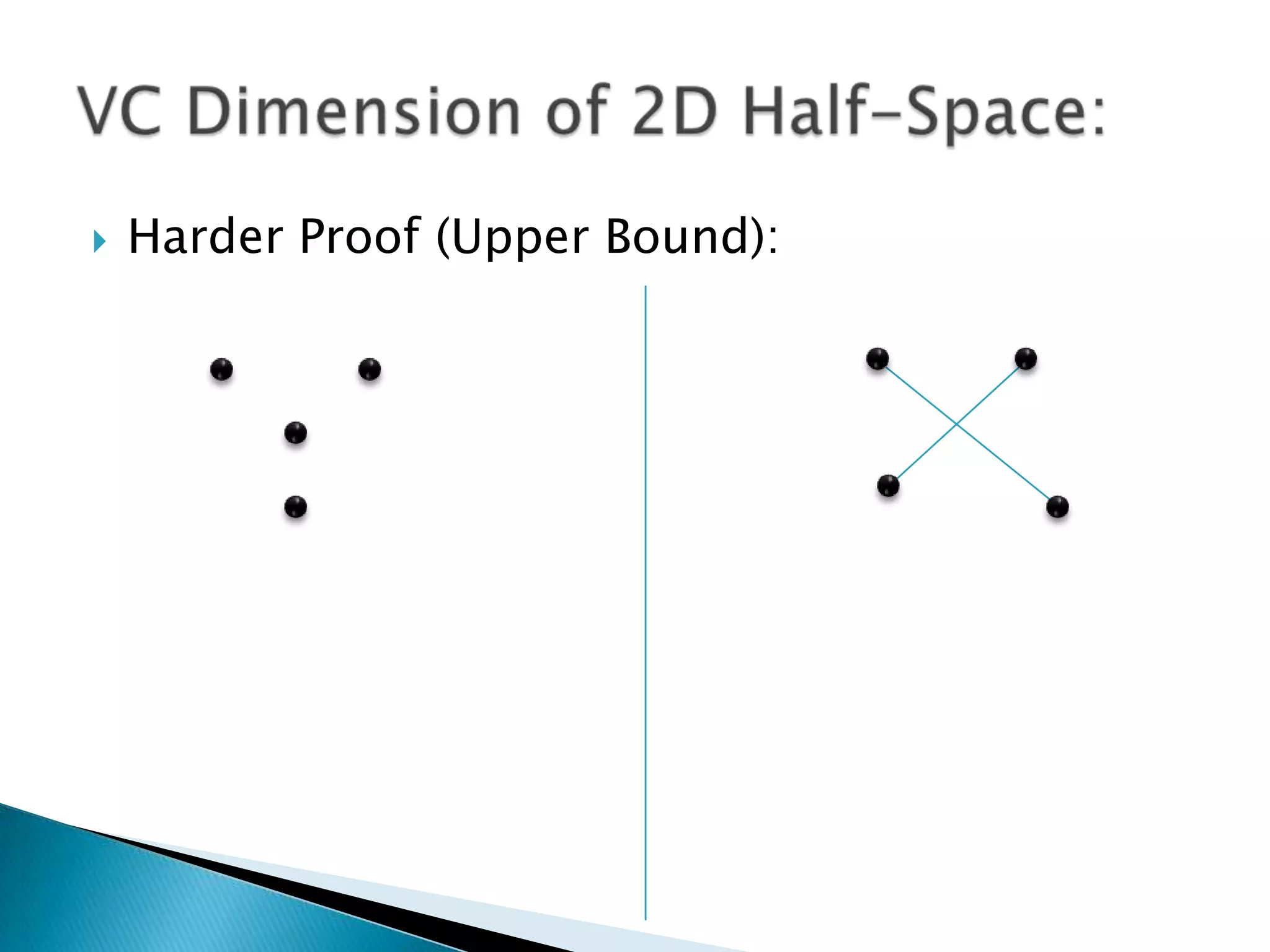
1) The document discusses PAC (probably approximately correct) learning and the VC (Vapnik-Chervonenkis) dimension. 2) The VC dimension measures the complexity of a hypothesis space or learning machine. It is defined as the maximum number of points that can be arranged so that the hypotheses shatter them, meaning every possible labeling of the points is represented by some hypothesis. 3) For linear classifiers of the form f(x) = sign(w·x + b) in R^d, the VC dimension is d+1. This provides an upper bound on the complexity of the hypothesis space.

1. PAC Learning and The VC DimensionTexPoint fonts used in EMF. Read the TexPoint manual before you delete this box.: AAAAA

2. Fix a rectangle (unknown to you):Rectangle GameFrom An Introduction to Computational Learning Theory by Keanrs and Vazirani

3. Draw points from some fixed unknown distribution:Rectangle Game

4. You are told the points and whether they are in or out:Rectangle Game

5. You propose a hypothesis:Rectangle Game

6. Your hypothesis is tested on points drawn from the same distribution:Rectangle Game

7. We want an algorithm that:With high probability will choose a hypothesis that is approximately correct.Goal

8. Choose the minimum area rectangle containing all the positive points:Minimum Rectangle Learner:h

9. How Good is this?RDerive a PAC bound:For fixed:R : RectangleD : Data Distributionε : Test Errorδ : Probability of failingm : Number of Samplesh

10. We want to show that with high probability the area below measured with respect to D is bounded by ε :Proof:< εRh

11. We want to show that with high probability the area below measured with respect to D is bounded by ε :Proof:< ε/4Rh

12. Proof:Define T to be the region that contains exactly ε/4 of the mass in D sweeping down from the top of R.p(T’) > ε/4 = p(T) IFFT’ contains TT’ contains T IFFnone of our m samples are from TWhat is the probabilitythat all samples miss TT’< ε/4TRh

13. Proof:What is the probability that all m samples miss T:What is the probability thatwe miss any of the rectangles?Union Bound T’< ε/4TRh

14. Union BoundBA

15. Proof:What is the probability that all m samples miss T:What is the probability thatwe miss any of therectangles:Union Bound = ε/4TRh

16. Proof:Probability that any region has weight greater than ε/4 after m samples is at most:If we fix m such that:Than with probability 1- δwe achieve an error rate of at most ε= ε/4TRh

17. Common Inequality:We can show:Obtain a lower bound on the samples:Extra Inequality

18. Provides a measure of the complexity of a “hypothesis space” or the “power” of “learning machine”Higher VC dimension implies the ability to represent more complex functionsThe VC dimension is the maximum number of points that can be arranged so that f shatters them.What does it mean to shatter?VC – Dimension

19. A classifier f can shatter a set of points if and only if for all truth assignments to those points f gets zero training errorExample: f(x,b) = sign(x.x-b)Define: Shattering

20. What is the VC Dimension of the classifier:f(x,b) = sign(x.x-b)Example Continued:

21. Conjecture:Easy Proof (lower Bound):VC Dimension of 2D Half-Space:

22. Harder Proof (Upper Bound):VC Dimension of 2D Half-Space:

23. VC Dimension Conjecture:VC-Dim: Axis Aligned Rectangles

24. VC Dimension Conjecture: 4Upper bound (more Difficult):VC-Dim: Axis Aligned Rectangles

25. General Half-Spaces in (d – dim)What is the VC Dimension of:f(x,{w,b})=sign( w . x + b )X in R^dProof (lower bound):Pick {x_1, …, x_n} (point) locations:Adversary gives assignments {y_1, …, y_n} and you choose {w_1, …, w_n} and b:

26. Extra Space:

27. General Half-SpacesProof (upper bound): VC-Dim = d+1Observe that the last d+1 points can always be expressed as:

28. Proof (upper bound): VC-Dim = d+1

29. Observe that the last d+1 points can always be expressed as:Extra Space