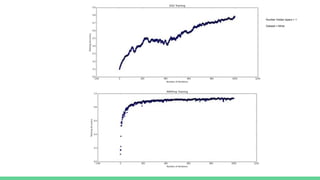
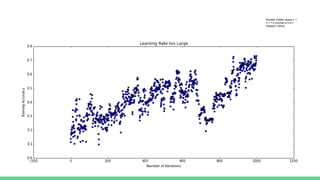
This document discusses various optimization techniques for training neural networks, including gradient descent, stochastic gradient descent, momentum, Nesterov momentum, RMSProp, and Adam. The key challenges in neural network optimization are long training times, hyperparameter tuning such as learning rate, and getting stuck in local minima. Momentum helps accelerate learning by amplifying consistent gradients while canceling noise. Adaptive learning rate algorithms like RMSProp, Adagrad, and Adam automatically tune the learning rate over time to improve performance and reduce sensitivity to hyperparameters.

1. Optimization in Deep
Learning
Jeremy Nixon

2. Overview
1. Challenges in Neural Network Optimization
2. Gradient Descent
3. Stochastic Gradient Descent
4. Momentum
a. Nesterov Momentum
5. RMSProp
6. Adam

3. Challenges in Neural Network Optimization
1. Training Time
a. Model complexity (depth, width) is important to accuracy
b. Training time for state of the art can take weeks on a GPU
2. Hyperparameter Tuning
a. Learning rate tuning is important to accuracy
3. Local Minima

4. Neural Net Refresh + Gradient Descent
w2
w1
Hidden raw / relu
output_softmax
x_train

5. Stochastic Gradient Descent
Dramatic Speedup
Sub-linear returns to more data in each batch
Crucial Learning Rate Hyperparameter
Schedule to reduce learning rate during training
SGD introduces noise to the gradient
Gradient will almost never fully converge to 0

6. Stochastic Gradient Descent

7. Number hidden layers = 1
lr = 1.0 (normal is 0.01)
Dataset = Mnist

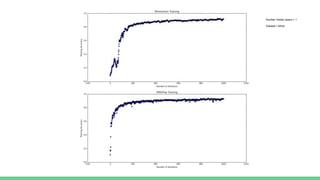
8. Momentum
Dramatically Accelerates Learning
1. Initialize learning rates & momentum matrix the size of the weights
2. At each SGD iteration, collect the gradient.
3. Update momentum matrix to be momentum rate times a momentum
hyperparameter plus the learning rate times the collected gradient.
s = .9 = momentum hyperparameter t.layers[i].moment1 = layer i’s momentum matrix lr = .01 gradient = sgd’s collected gradient

9. Number hidden layers = 2
Dataset = Mnist

10. Intuition for Momentum
Automatically cancels out noise in the gradient
Amplifies small but consistent gradients
“Momentum” derives from the physical analogy [momentum = mass * velocity]
Assumes unit mass
Velocity vector is the ‘particle's’ momentum
Deals well with heavy curvature

11. Momentum Accelerates the Gradient
Gradient that accumulates in the same direction can achieve velocities of up to
lr / (1-s). S = .9 => lr can max out at lr * 10 in the direction of accumulated gradient.

12. Asynchronous SGD similar to Momentum
In distributed SGD, asynchronous has workers update parameters as they return, instead of
waiting for all workers to finish
Creates a weighted average of previous gradients applied to the current weights

13. Nesterov Momentum
Evaluate the gradient with the momentum step taken into account

14. Number hidden layers = 2
Dataset = Mnist

15. Adaptive Learning Rate Algorithms
Adagrad
Duchi et al., 2011
RMSProp
Hinton, 2012
Adam
Kingma and Ba, 2014
Idea is to auto-tune the learning rate, making the network less sensitive to hyperparameters.

16. Adagrad
Shrinks the learning rate adaptively
Learning rate is the inverse of the historical squared gradient
r = squared gradient history g = gradient theta = weights epsilon = learning rate delta = small constant for numerical stability

17. Intuition for Adagrad
Instead of setting a single global learning rate, have a different learning rate for
every weight in the network
Parameters with the largest derivative have a rapid decrease in learning rate
Parameters with small derivatives have a small decrease in learning rate
We get much more progress in more gently sloped directions of parameter
space.
Downside - accumulating gradients from the beginning leads to extremely small
learning rates later in training
Downside - doesn’t deal well with differences in global and local structure

18. RMSProp
Collect exponentially weighted average of the gradient for the learning rate
Performs well in non-convex setting with differences between global and local
structure
Can be combined with momentum / nesterov momentum

19. Number hidden layers = 1
Dataset = Mnist

20. Number hidden layers = 1
Dataset = Mnist

21. Adam
Short for “Adaptive Moments”
Exponentially weighted average of gradient for momentum (first moment)
Exponentially weighted average of squared gradient for adapting learning rate
(second moment)
Bias Correction for both to adjust early in training

22. Adam

23. Number hidden layers = 5
Dataset = Mnist

24. Thank you!
Questions?
Bibliography
Adam paper - https://arxiv.org/abs/1412.6980
Adagrad - http://jmlr.org/papers/v12/duchi11a.html
RMSProp - http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
Deep Learning Textbook - http://www.deeplearningbook.org/