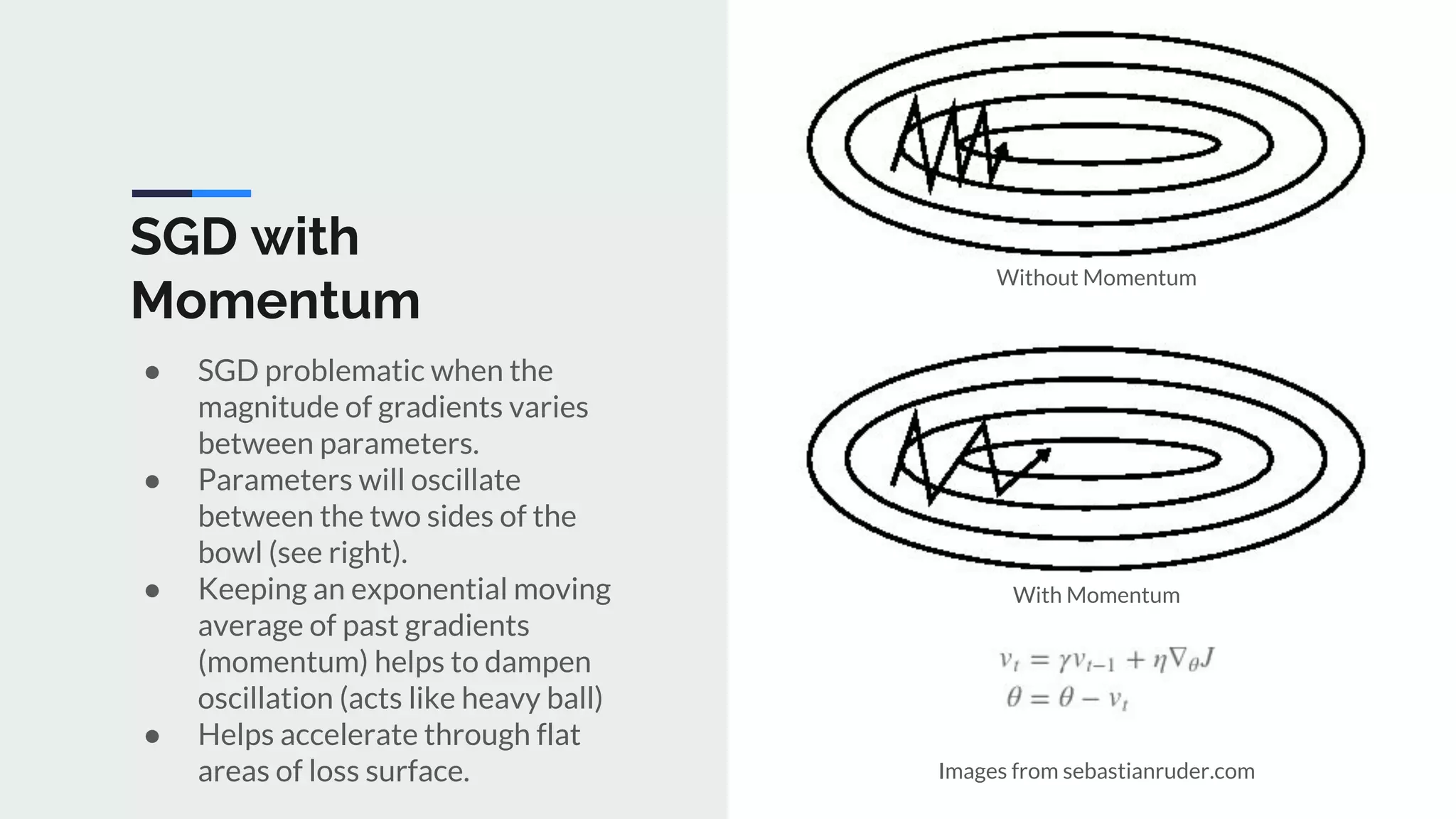
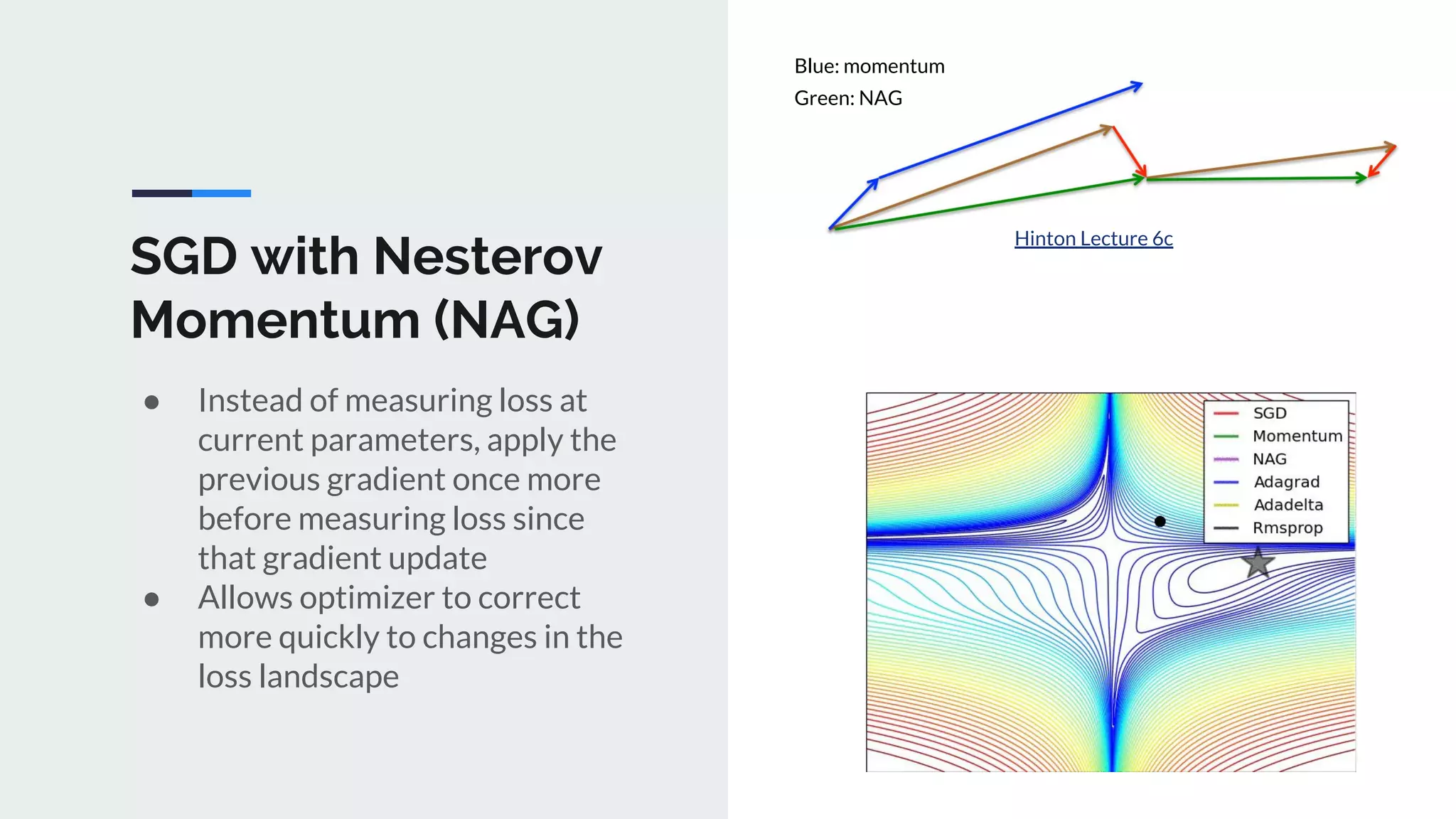
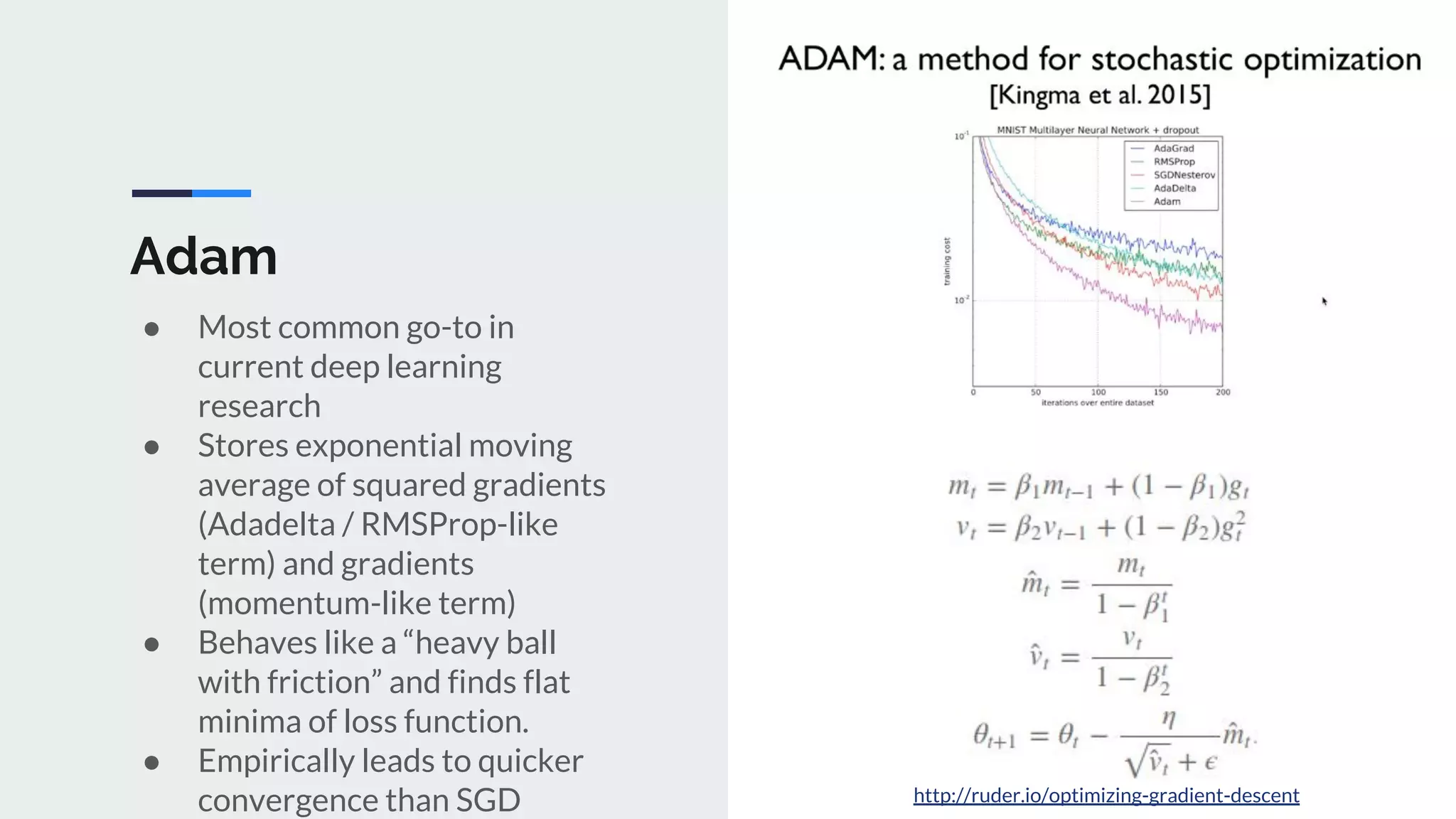
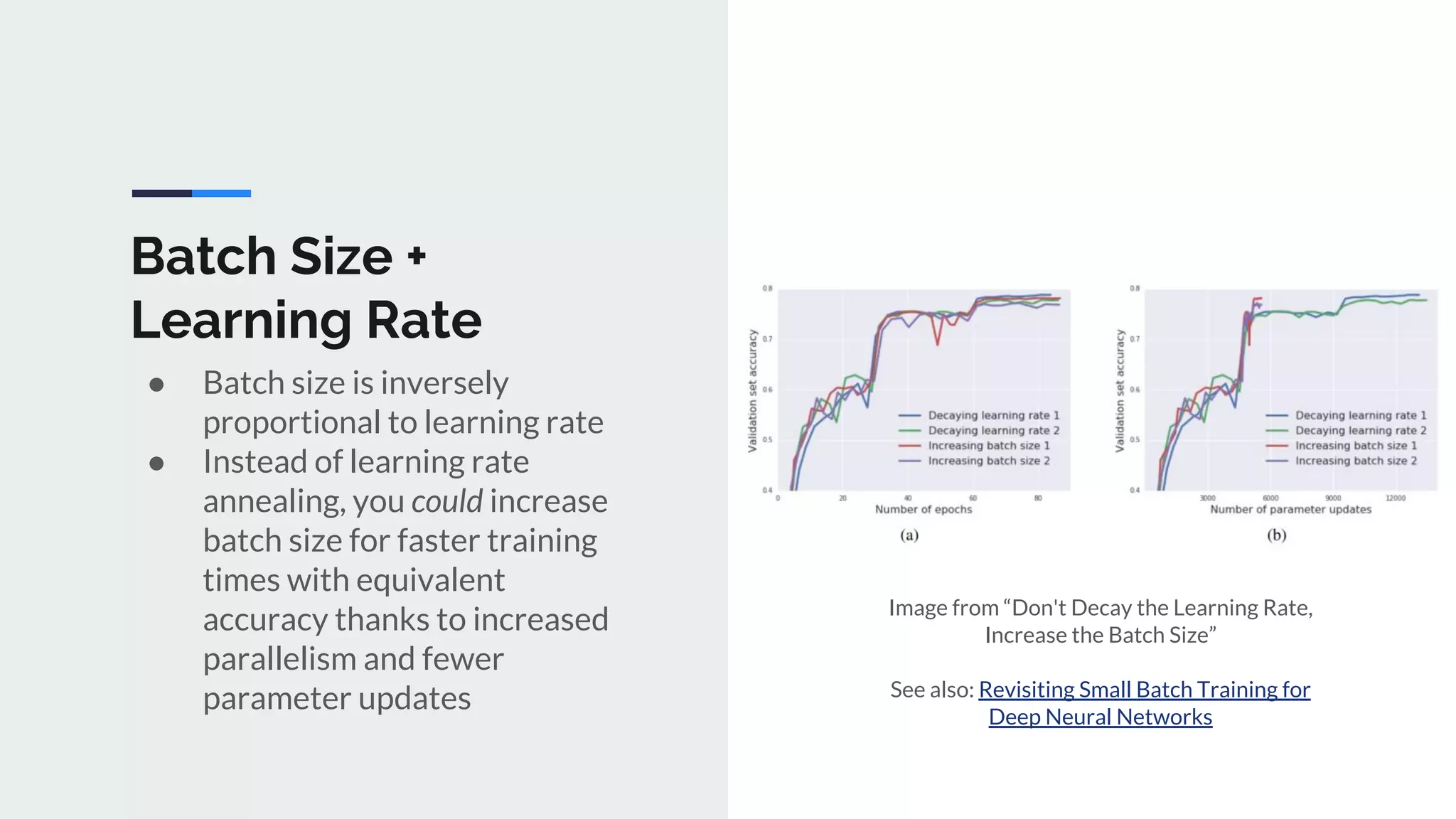
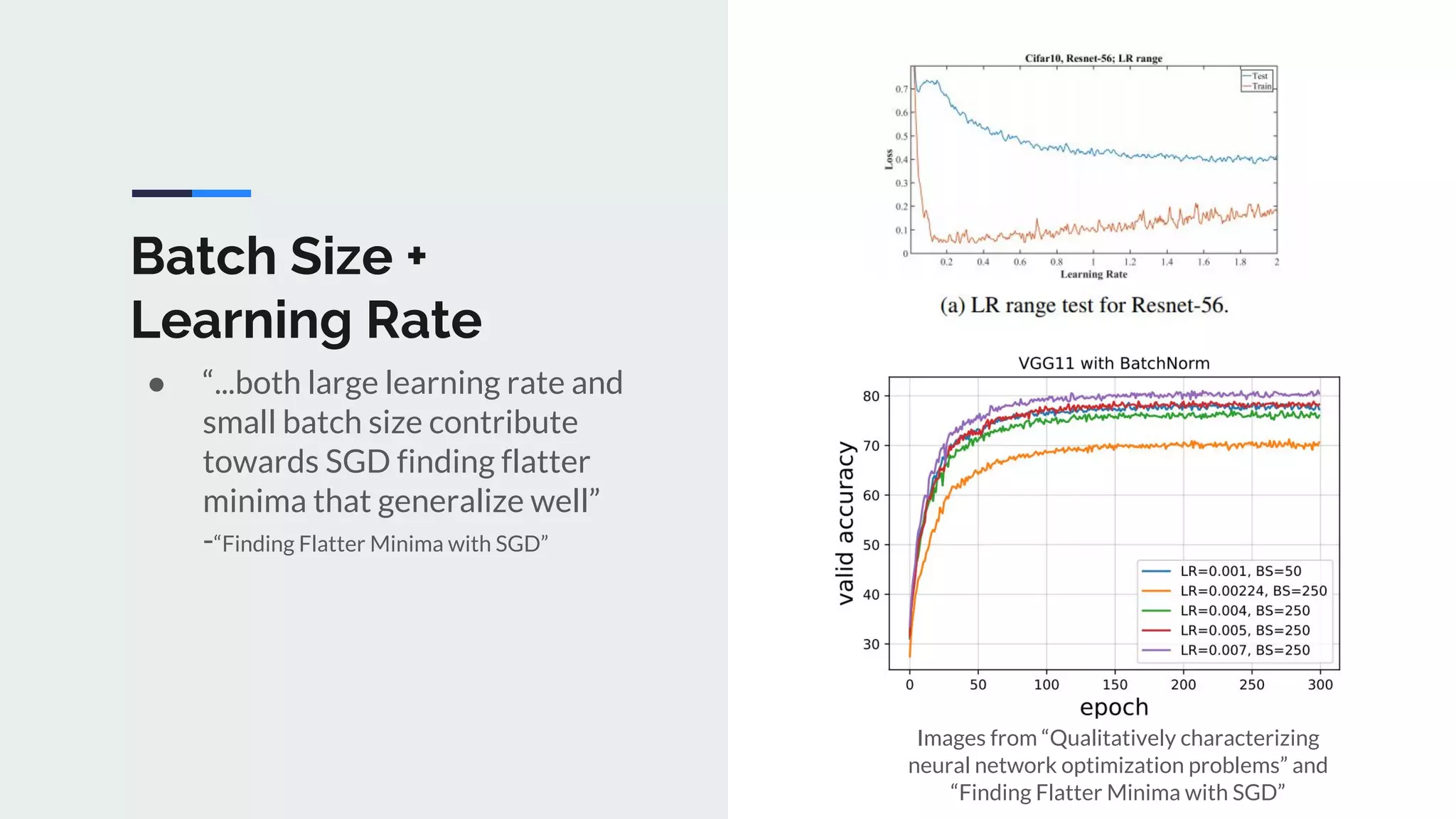
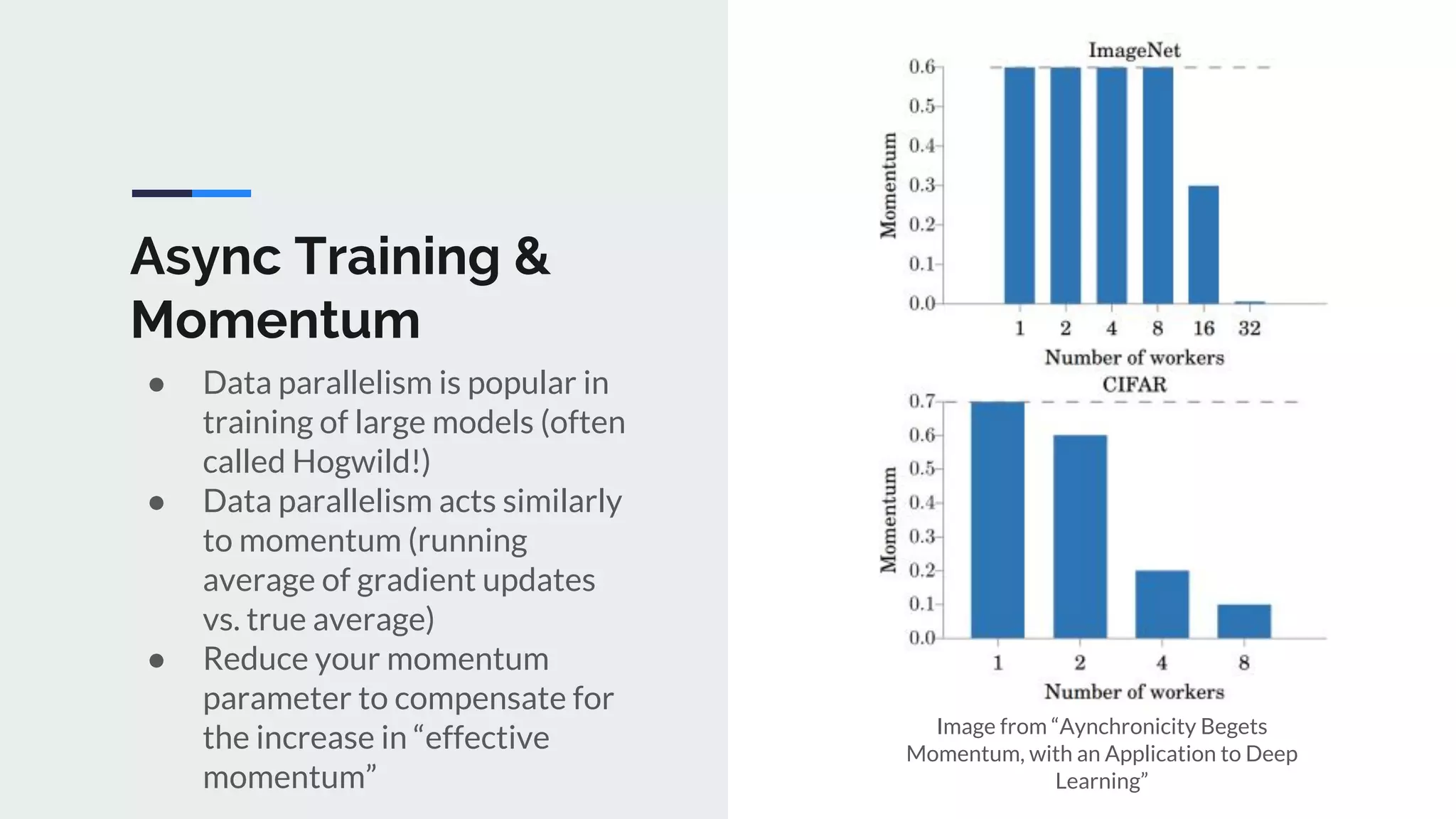
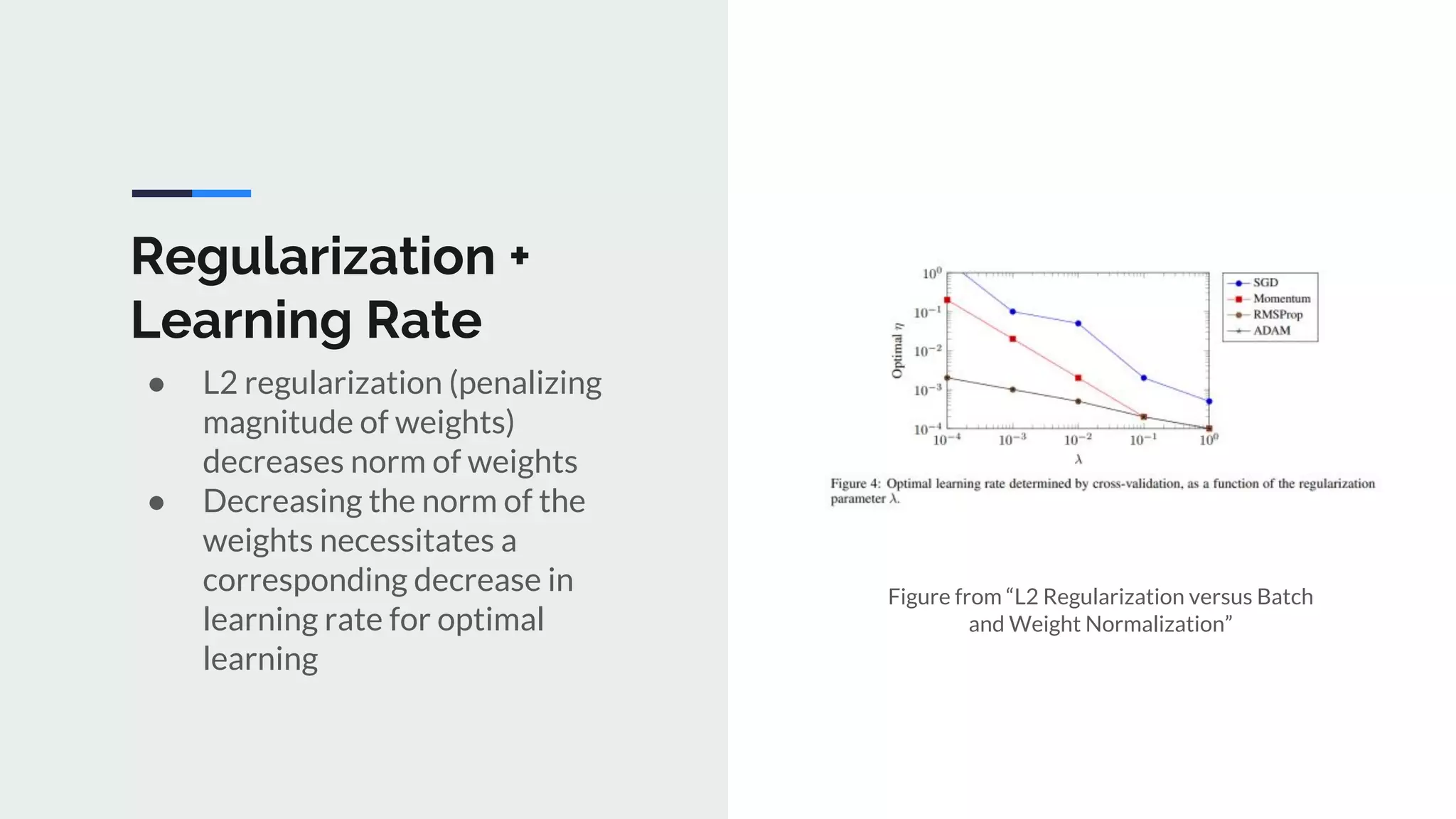
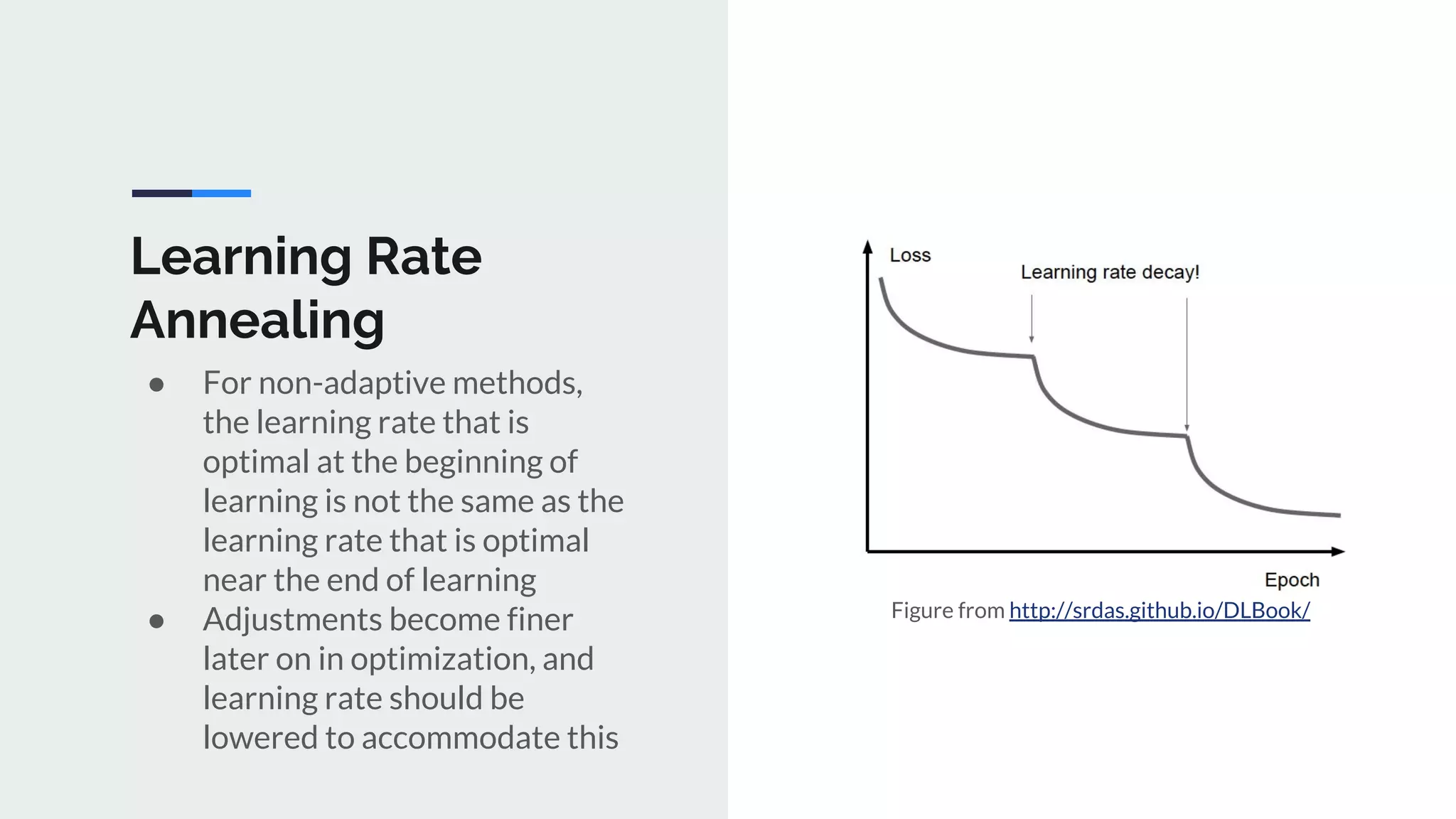
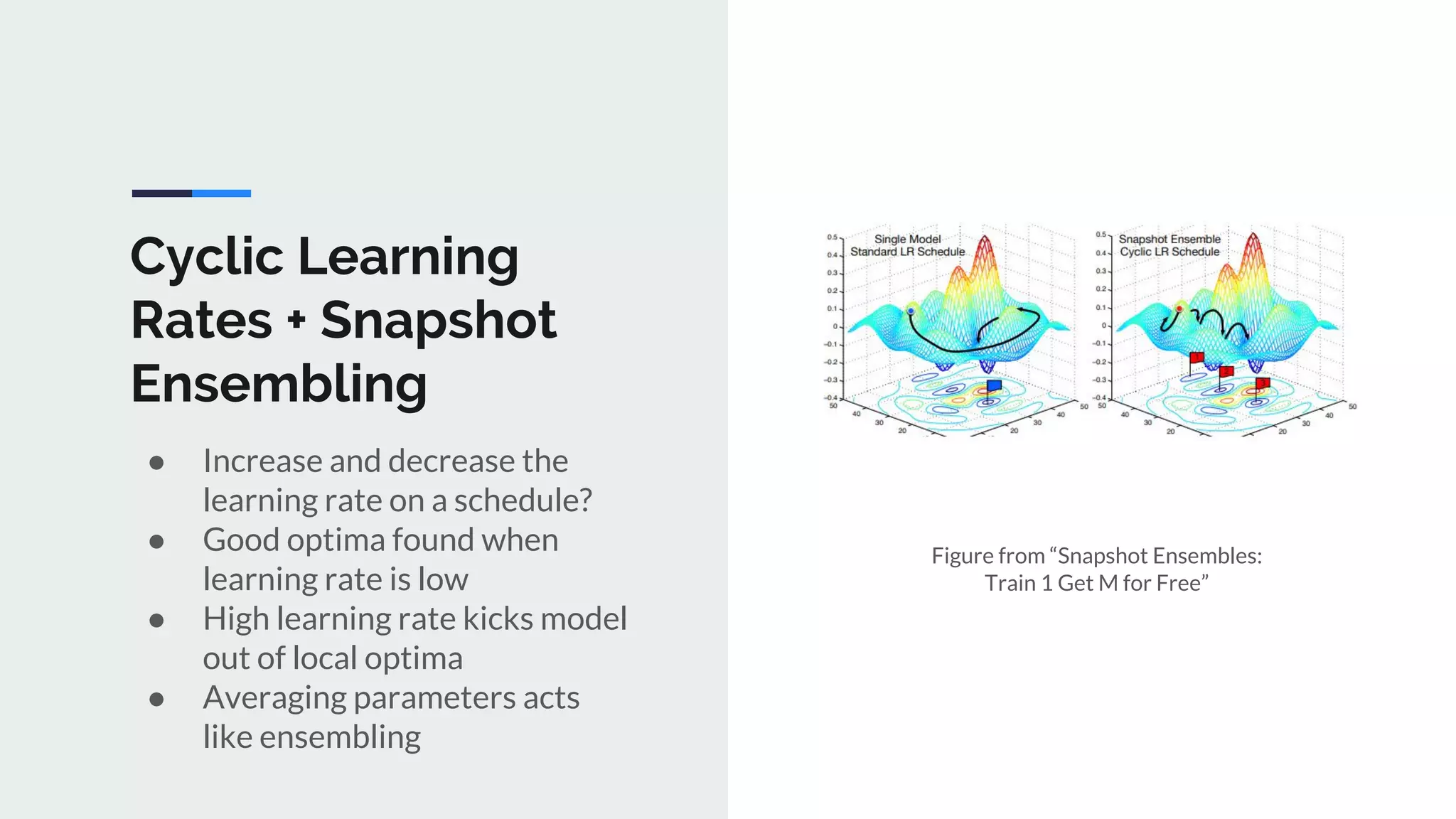
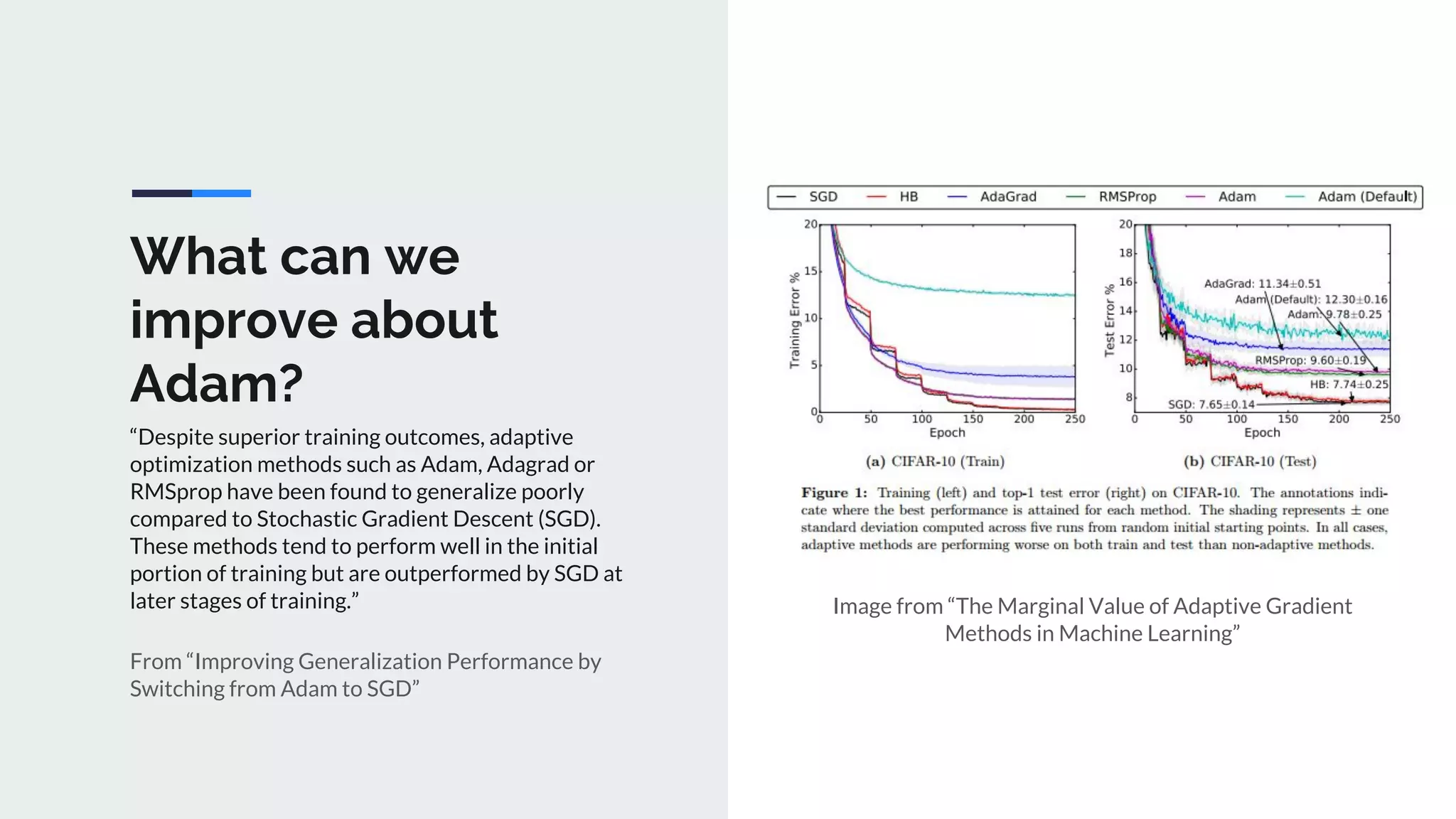
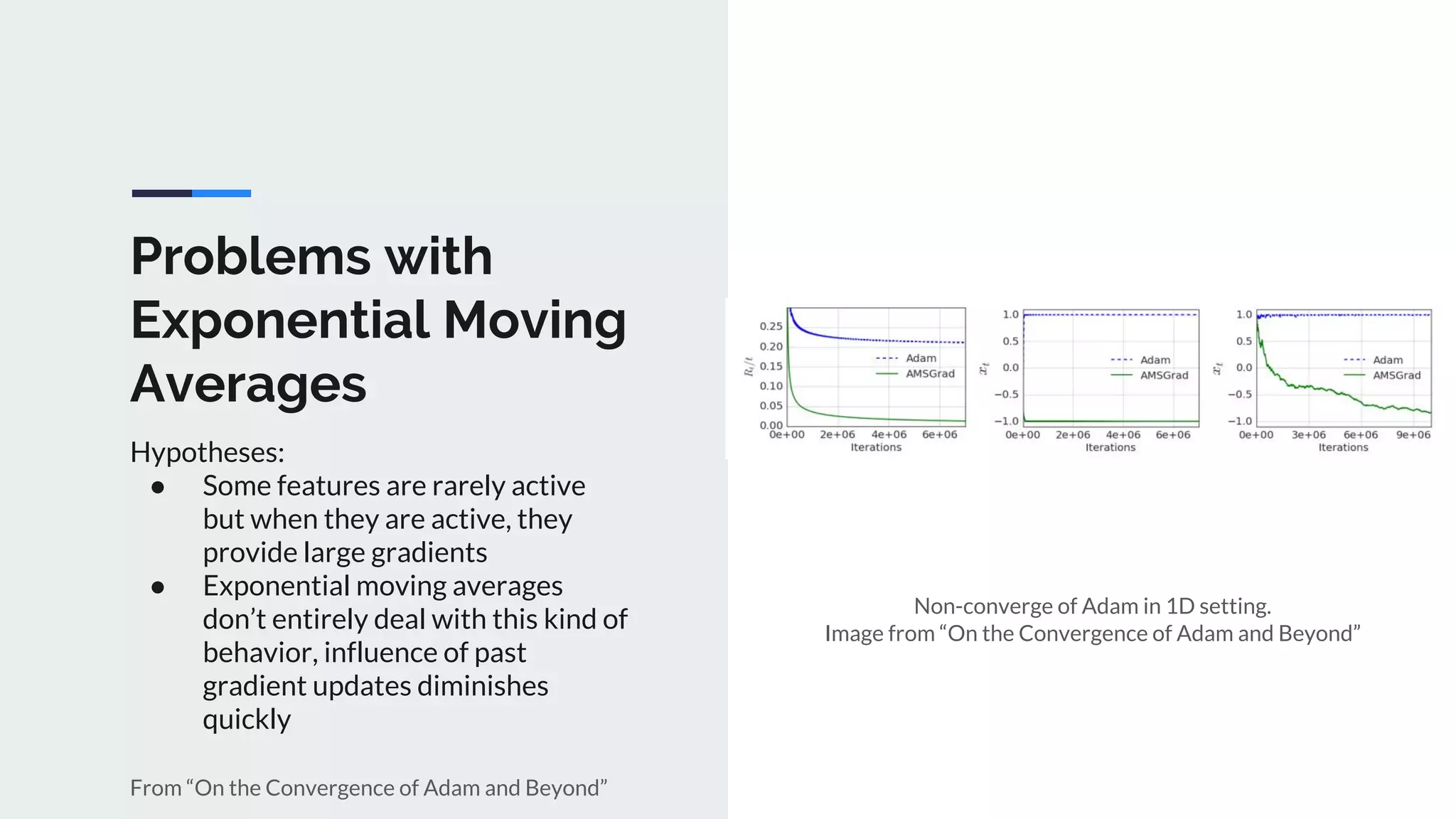
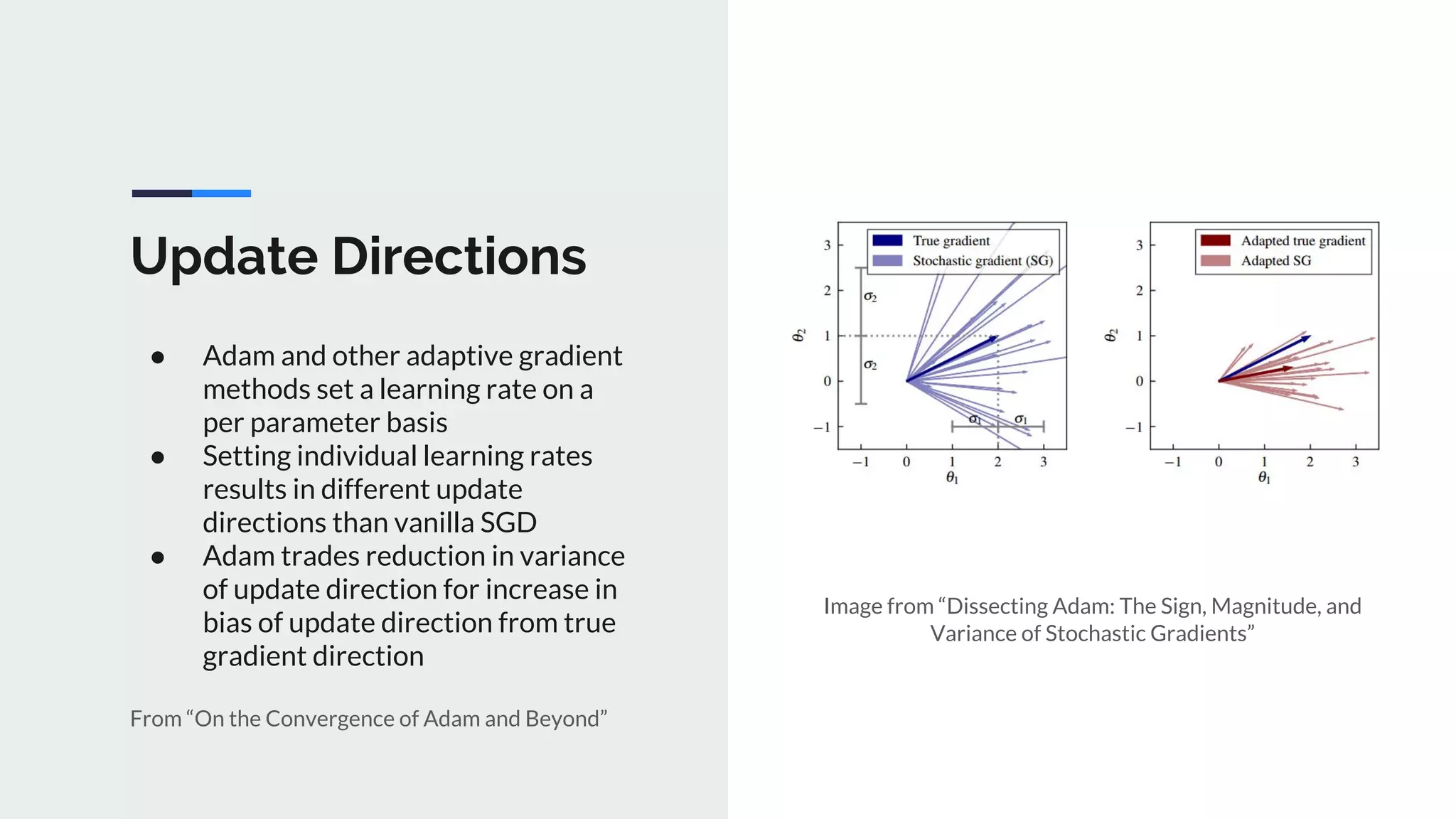
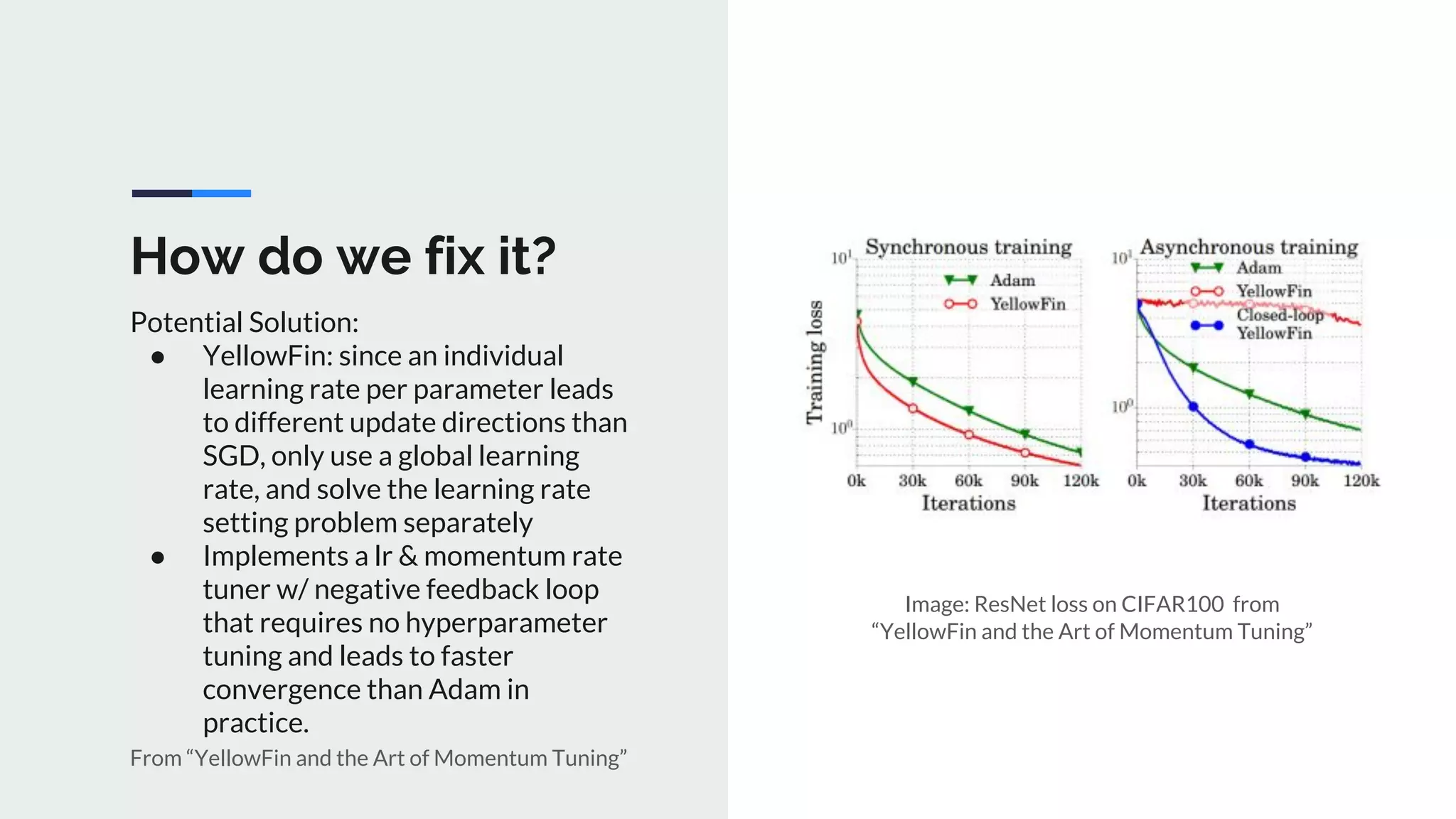
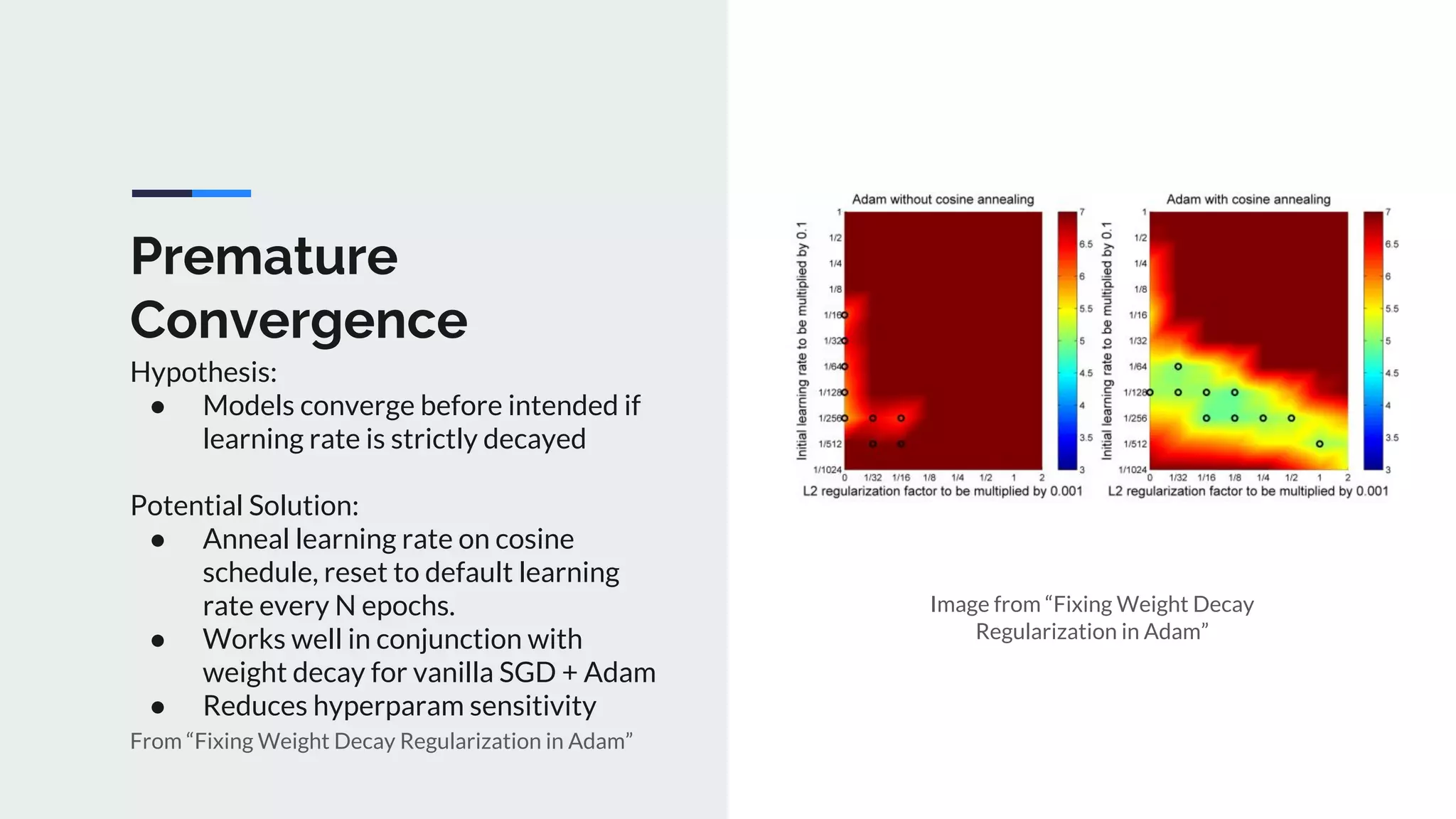
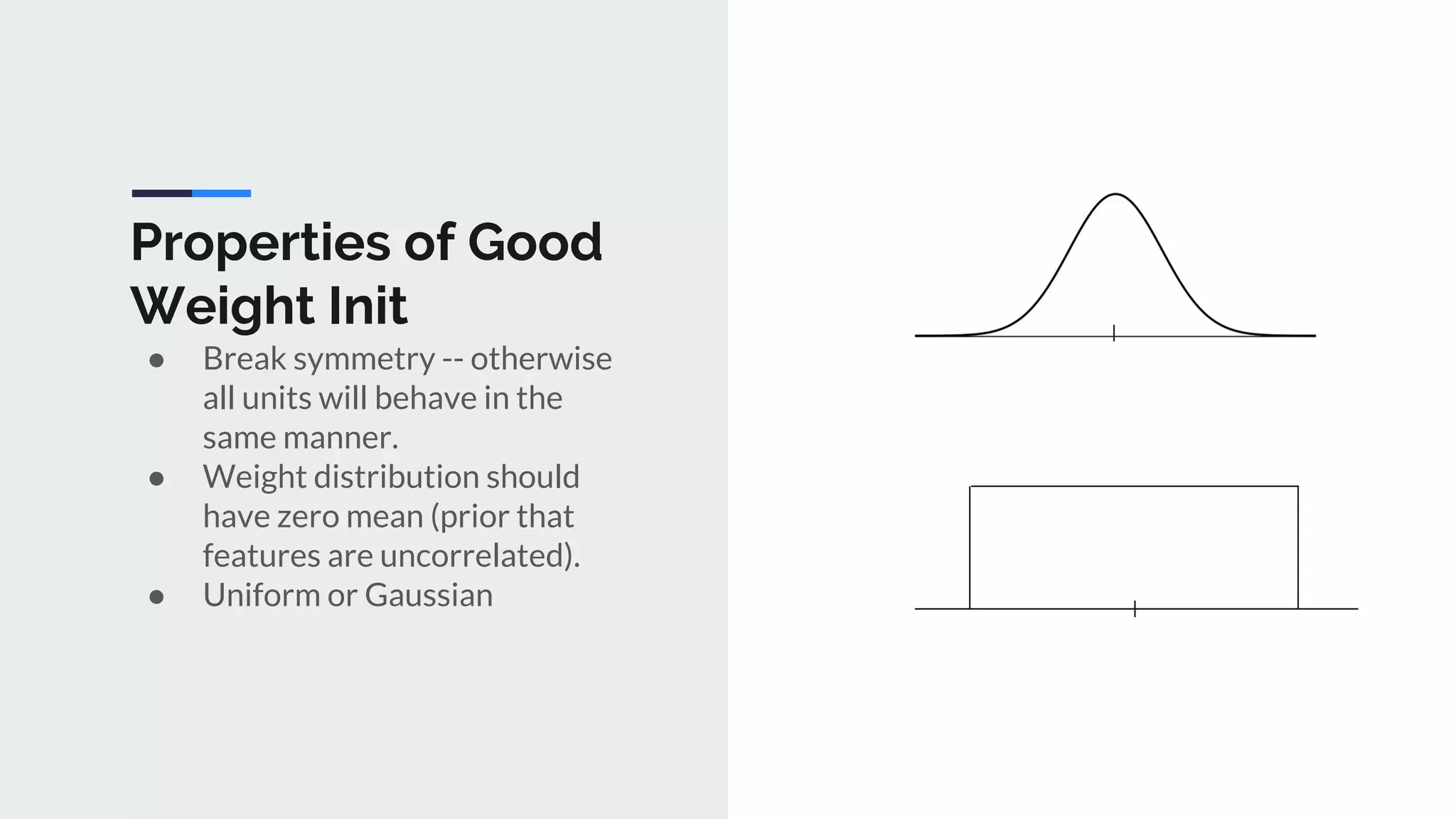
The document provides an extensive overview of optimization techniques in machine learning, particularly focusing on gradient descent methods such as SGD, momentum, and Adam. It discusses the benefits of adjustments like learning rate scheduling and batch size variations, as well as potential issues with adaptive methods and strategies for improvement. Key takeaways include the importance of parameter initialization, the need for careful consideration of hyperparameters, and ongoing developments in the field of optimization.

1. Everything You Wanted to
Know about Optimization
(and some you didn’t)
Madison May
madison@indico.io

2. Madison May
Machine Learning Architect @ Indico Data Solutions
Solve big problems with small data.
Email: madison@indico.io
Twitter: @pragmaticml
Github: @madisonmay

3. Ancient History
(an optimization primer)

4. Definitions:
● Loss: differentiable measure
of model error
● Gradient: direction of
steepest descent at point on
error surface
● Loss surface: how loss varies
with parameter value
● Learning rate: how far to
move params in direction of
gradient

5. Gradient descent
● Compute loss on entire
dataset
● Compute gradient of
parameters with respect to
loss
● Update parameters in the
direction of the gradient
scaled by some parameter
(the learning rate)

6. SGD
(mini-batch
gradient descent)
● Compute loss on small
number of examples
● Compute gradient of
parameters with respect to
loss
● Update parameters in the
direction of the gradient
scaled by some parameter
(the learning rate)

7. Mini-batch vs. Full
● Don’t need to compute the
gradient on all of your training
examples to get a gradient
estimate that is good enough.
● Better to update your
parameters more frequently
with noisy gradient than get a
perfect gradient estimate and
update model params less.
● Stochastic gradient estimates
help avoid local minima /
saddle points
https://en.wikipedia.org/wiki/gradient_descen
t

8. SGD with
Momentum
● SGD problematic when the
magnitude of gradients varies
between parameters.
● Parameters will oscillate
between the two sides of the
bowl (see right).
● Keeping an exponential moving
average of past gradients
(momentum) helps to dampen
oscillation (acts like heavy ball)
● Helps accelerate through flat
areas of loss surface. Images from sebastianruder.com
With Momentum
Without Momentum

9. SGD with Nesterov
Momentum (NAG)
● Instead of measuring loss at
current parameters, apply the
previous gradient once more
before measuring loss since
that gradient update
● Allows optimizer to correct
more quickly to changes in the
loss landscape
Hinton Lecture 6c
Blue: momentum
Green: NAG

10. Adagrad, Adadelta,
And RMSProp
● Different parameters require
differently scaled updates
● Values of previous gradients
are used to scale the current
gradient estimate in a
heuristic manner
● Significantly less sensitive to
hyperparameters thanks to
per parameter scaling

11. Adam
● Most common go-to in
current deep learning
research
● Stores exponential moving
average of squared gradients
(Adadelta / RMSProp-like
term) and gradients
(momentum-like term)
● Behaves like a “heavy ball
with friction” and finds flat
minima of loss function.
● Empirically leads to quicker
convergence than SGD http://ruder.io/optimizing-gradient-descent

12. Takeaways
● SGD: update params by scaling gradient
● Momentum: incorporating exponential moving
averages of gradient value allow for SGD to escape
saddle points. Acts like acceleration of ball on surface
due to mass.
● Adadelta / RMSprop: inverse scaling by exponential
moving average of square of gradient to help with
sensitivity to hyperparameters
● Adam: incorporates elements of momentum and
Adadelta / RMSprop

13. Async Training, Batch Size,
and Regularization Affect
Learning Rate Dynamics

14. Batch Size +
Learning Rate
● Batch size is inversely
proportional to learning rate
● Instead of learning rate
annealing, you could increase
batch size for faster training
times with equivalent
accuracy thanks to increased
parallelism and fewer
parameter updates
Image from “Don't Decay the Learning Rate,
Increase the Batch Size”
See also: Revisiting Small Batch Training for
Deep Neural Networks

15. Batch Size +
Learning Rate
● “...both large learning rate and
small batch size contribute
towards SGD finding flatter
minima that generalize well”
-“Finding Flatter Minima with SGD”
Images from “Qualitatively characterizing
neural network optimization problems” and
“Finding Flatter Minima with SGD”

16. Async Training &
Momentum
● Data parallelism is popular in
training of large models (often
called Hogwild!)
● Data parallelism acts similarly
to momentum (running
average of gradient updates
vs. true average)
● Reduce your momentum
parameter to compensate for
the increase in “effective
momentum”
Image from “Aynchronicity Begets
Momentum, with an Application to Deep
Learning”

17. Regularization +
Learning Rate
● L2 regularization (penalizing
magnitude of weights)
decreases norm of weights
● Decreasing the norm of the
weights necessitates a
corresponding decrease in
learning rate for optimal
learning
Figure from “L2 Regularization versus Batch
and Weight Normalization”

18. Takeaways
● There’s a difference between the learning rate
parameter and the effective learning rate of models
● Understand how batch size, async training, and the
norm of model parameters interact with learning rate
for best results.

19. Learning Rate Scheduling

20. Learning Rate
Annealing
● For non-adaptive methods,
the learning rate that is
optimal at the beginning of
learning is not the same as the
learning rate that is optimal
near the end of learning
● Adjustments become finer
later on in optimization, and
learning rate should be
lowered to accommodate this
Figure from http://srdas.github.io/DLBook/

21. Cyclic Learning
Rates + Snapshot
Ensembling
● Increase and decrease the
learning rate on a schedule?
● Good optima found when
learning rate is low
● High learning rate kicks model
out of local optima
● Averaging parameters acts
like ensembling
Figure from “Snapshot Ensembles:
Train 1 Get M for Free”

22. Takeaways
● Use learning rate annealing when using vanilla SGD or
SGD w/ momentum
● Consider snapshot ensembling for easy incremental
model performance improvements.

23. Improving Adam

24. ICLR 2018 Optimization Papers
● On the convergence of Adam and beyond (Sashank J. Reddi, Satyen Kale, Sanjiv Kumar)
● Normalized, direction-preserving Adam (Zijun Zhang, Lin Ma, Zongpeng Li, Chuan Wu)
● Fixing Weight Decay Regularization in Adam (Ilya Loshchilov, Frank Hutter)
● Dissecting Adam: The Sign, Magnitude and Variance of Stochastic Gradients (Lukas Balles, Philipp
Hennig)
● YellowFin and the Art of Momentum Tuning (Jian Zhang, Ioannis Mitliagkas, Christopher Re)

25. What can we
improve about
Adam?
“Despite superior training outcomes, adaptive
optimization methods such as Adam, Adagrad or
RMSprop have been found to generalize poorly
compared to Stochastic Gradient Descent (SGD).
These methods tend to perform well in the initial
portion of training but are outperformed by SGD at
later stages of training.”
From “Improving Generalization Performance by
Switching from Adam to SGD”
Image from “The Marginal Value of Adaptive Gradient
Methods in Machine Learning”

26. Problems with
Exponential Moving
Averages
Hypotheses:
● Some features are rarely active
but when they are active, they
provide large gradients
● Exponential moving averages
don’t entirely deal with this kind of
behavior, influence of past
gradient updates diminishes
quickly
From “On the Convergence of Adam and Beyond”
Non-converge of Adam in 1D setting.
Image from “On the Convergence of Adam and Beyond”

27. How do we fix it?
Potential Solution:
● Instead of storing exponential
moving average of past squared
gradients, store the maximum past
squared gradient and use that to
adjust size of weight update
● Resultant algorithm is termed
“AMSGrad”
● Enjoys theoretical guarantees that
were missing from Adam.
● Empirically leads to better
generalization performance
From “On the Convergence of Adam and Beyond”
Image from
http://ruder.io/deep-learning-optimization-2017

28. Other potential
problems
Hypotheses:
● “When combined with adaptive
gradients, L2 regularization leads to
weights with large gradients being
regularized less than they would be
when using weight decay.”
● In other words, using L2
regularization in conjunction with
Adam is not effective -- although
weight decay is.
From “Fixing Weight Decay Regularization in Adam”
Image from “Fixing Weight Decay Regularization in
Adam”

29. How do we fix it?
Potential Solution:
● Use weight decay as originally
formulated rather than L2
normalization
From “Fixing Weight Decay Regularization in Adam”
Image from “Fixing Weight Decay Regularization in
Adam”

30. Update Directions
● Adam and other adaptive gradient
methods set a learning rate on a
per parameter basis
● Setting individual learning rates
results in different update
directions than vanilla SGD
● Adam trades reduction in variance
of update direction for increase in
bias of update direction from true
gradient direction
From “On the Convergence of Adam and Beyond”
Image from “Dissecting Adam: The Sign, Magnitude, and
Variance of Stochastic Gradients”

31. How do we fix it?
Potential Solution:
● YellowFin: since an individual
learning rate per parameter leads
to different update directions than
SGD, only use a global learning
rate, and solve the learning rate
setting problem separately
● Implements a lr & momentum rate
tuner w/ negative feedback loop
that requires no hyperparameter
tuning and leads to faster
convergence than Adam in
practice.
From “YellowFin and the Art of Momentum Tuning”
Image: ResNet loss on CIFAR100 from
“YellowFin and the Art of Momentum Tuning”

32. Takeaways
● Adam generally performs well but has its limits
● Use with weight decay rather than L2 regularization
● At the upper extremes of training data availability try
SGD + nesterov momentum + learning rate annealing
or YellowFin.
● Compare against AMSGrad
● Monitor arxiv.org and wait 6 months -- academia is still
deciding on whether it’s time to move past Adam.

33. Other considerations
● Weight initialization
● Batch norm / Layer norm

34. Shoutouts
● Sebastian Ruder has blogged extensively about
optimization -- his content forms the basis for much of
this talk
○ http://ruder.io/optimizing-gradient-descent/
○ http://ruder.io/deep-learning-optimization-2017
/
● Chapter 8 of “Deep Learning” by Goodfellow, Bengio,
and Courville was a useful supplement
○ https://www.deeplearningbook.com
● Fei Fei Li’s CS231N course at Stanford:
○ http://cs231n.github.io/neural-networks-3

35. Questions?

36. Appendix

37. Premature
Convergence
Hypothesis:
● Models converge before intended if
learning rate is strictly decayed
Potential Solution:
● Anneal learning rate on cosine
schedule, reset to default learning
rate every N epochs.
● Works well in conjunction with
weight decay for vanilla SGD + Adam
● Reduces hyperparam sensitivity
From “Fixing Weight Decay Regularization in Adam”
Image from “Fixing Weight Decay
Regularization in Adam”

38. Weight Initialization

39. Properties of Good
Weight Init
● Break symmetry -- otherwise
all units will behave in the
same manner.
● Weight distribution should
have zero mean (prior that
features are uncorrelated).
● Uniform or Gaussian

40. Other Weight Init
Considerations
● Glorot initialization -- scaling
based on number of layer
inputs / outputs
● He initialization -- scaling
weight norm based on
number of layer inputs, for
ReLU activation
● Goal: preserve relative scale
of activation variance and
gradient variance through
many layers
Glorot Uniform
He Initialization

41. Takeaways
● Parameter initialization matters (more than you might
think)
● Take care to ensure that activation and gradient
variances stay roughly constant throughout layers
when training deep networks (consider visualization)