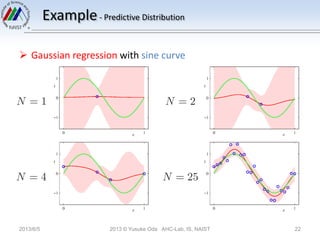
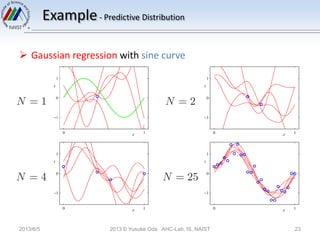
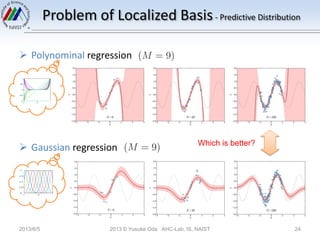
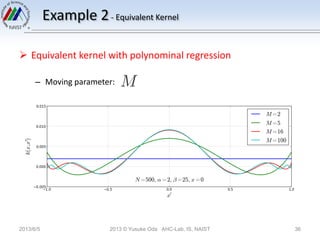
The document discusses Bayesian linear regression. It introduces the parameter distribution by assuming a Gaussian prior distribution for the model parameters. This leads to a Gaussian posterior distribution. It then discusses the predictive distribution for new data points by marginalizing over the posterior distribution of the parameters. Finally, it introduces the concept of an equivalent kernel, which allows predictions to be written as a linear combination of the training targets using a kernel matrix rather than by calculating the model parameters.