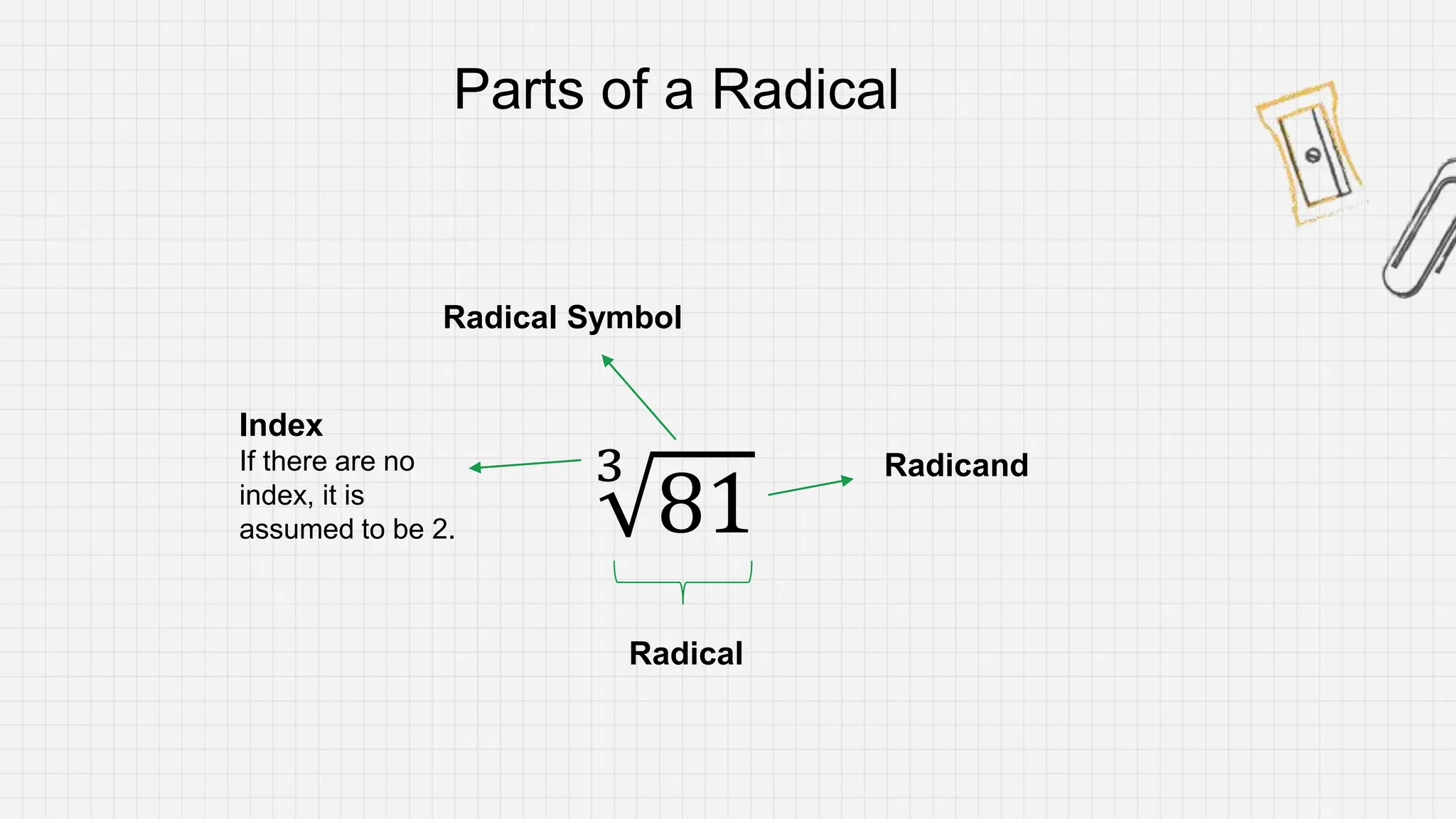
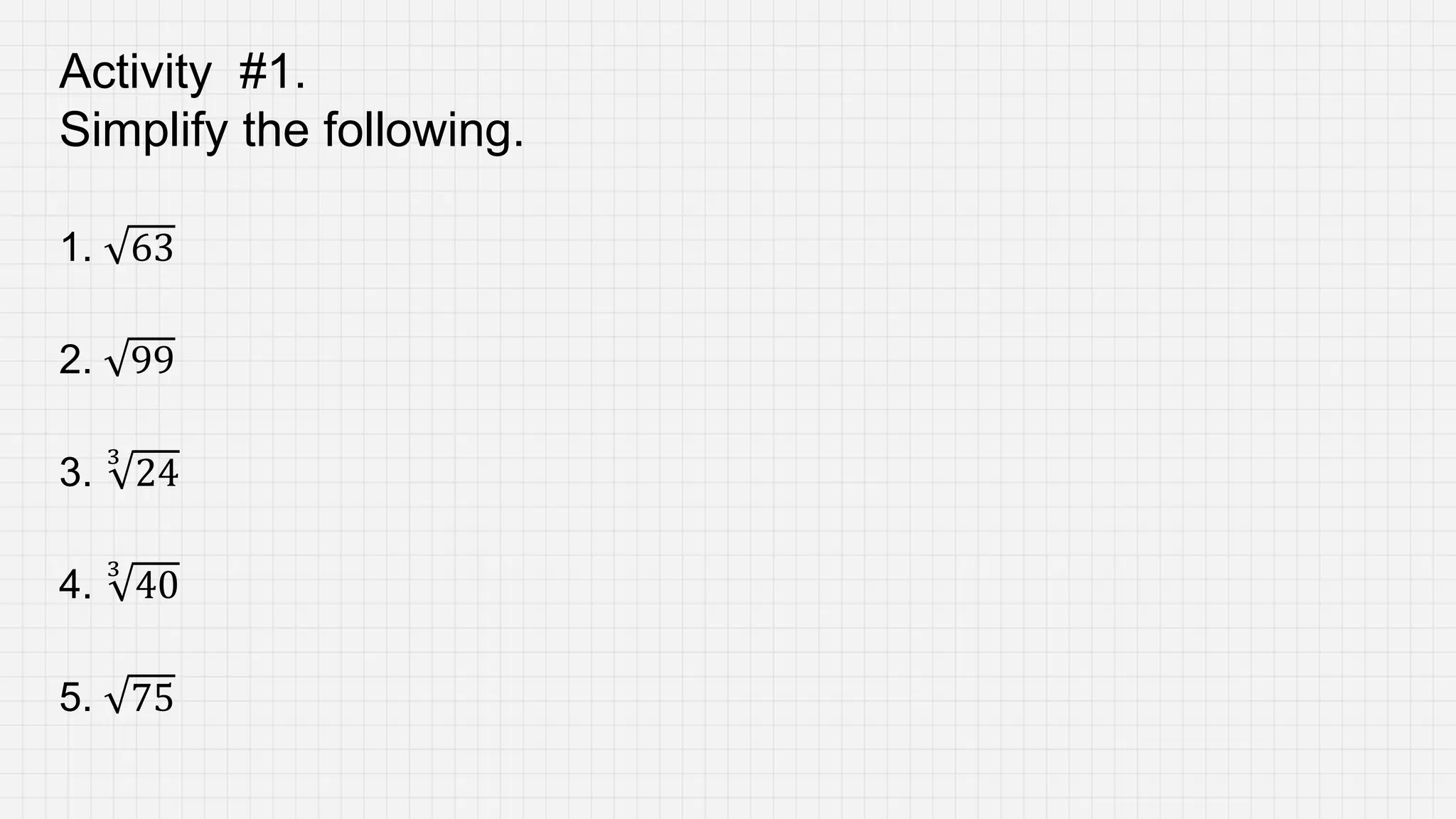
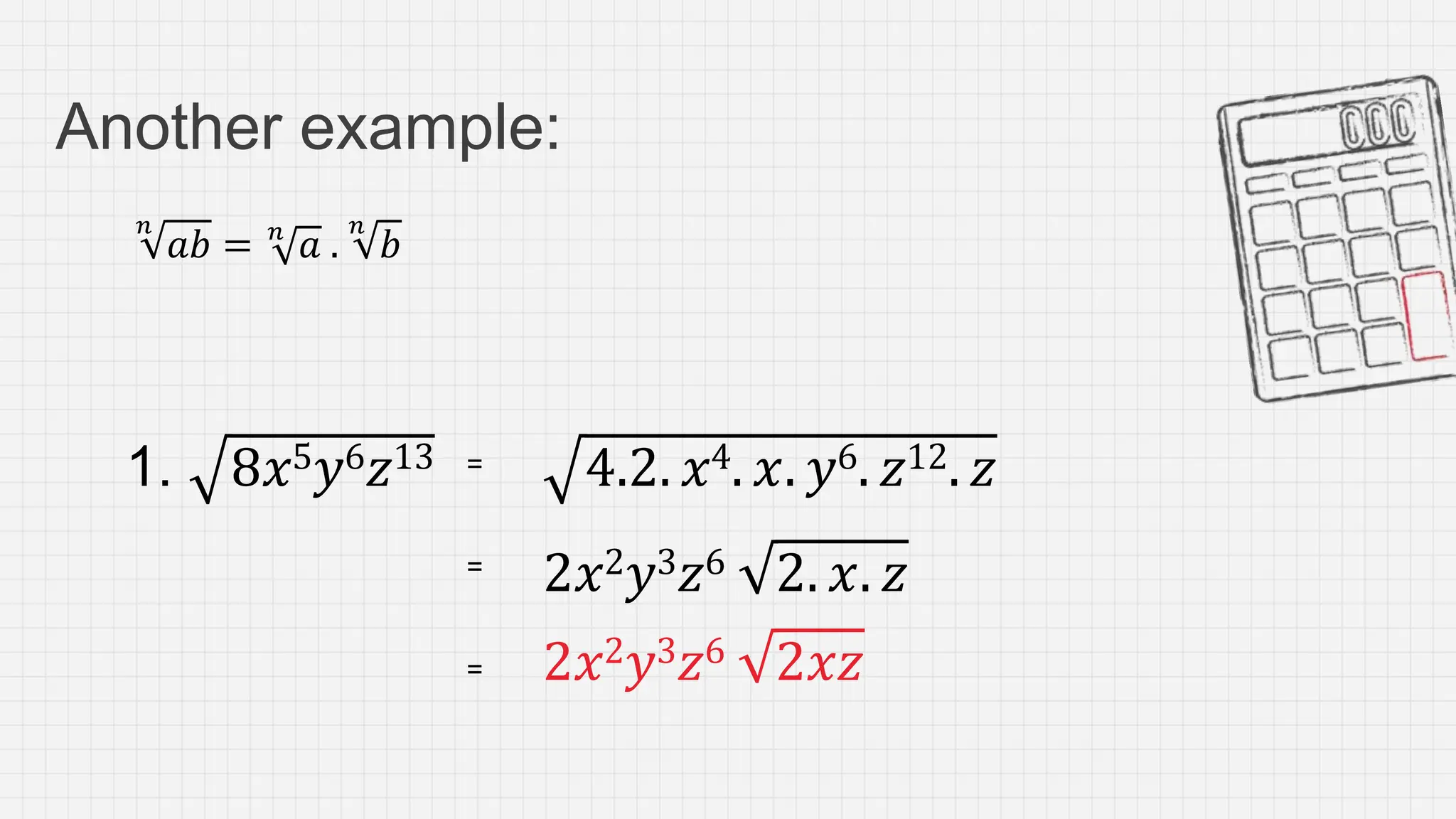The document discusses laws and properties of radicals that can be used to simplify radical expressions. It defines key terms like radicand, index, and conjugate. It provides examples of simplifying radicals by reducing the radicand and order of radicals, rationalizing denominators, and adding/subtracting like and unlike radicals. The objective is to use these laws and techniques to simplify radical expressions into their simplest forms.