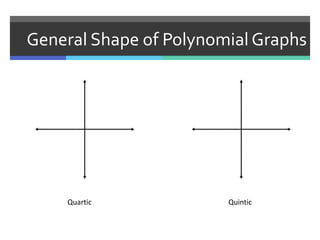
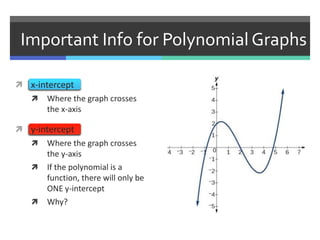
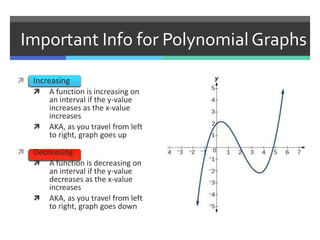
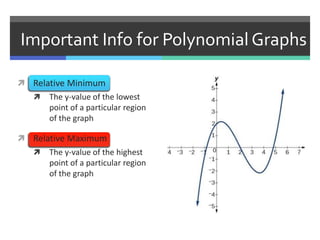
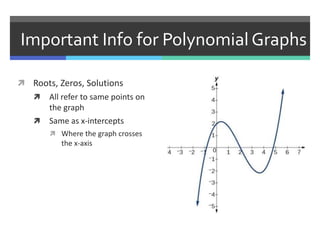
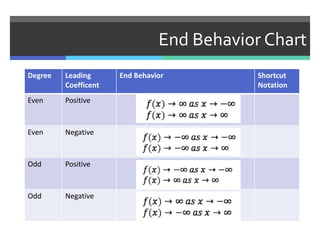
This document discusses polynomials and their graphs. It defines a polynomial as an expression with two or more algebraic terms separated by plus and minus signs. Polynomials are named based on their degree and number of terms, with the degree being the highest exponent of its terms. The general shapes of polynomial graphs are constant for linear polynomials, parabolic for quadratics, cubic for cubics, and so on. Important features of polynomial graphs discussed include x-intercepts, y-intercepts, regions of increase/decrease, relative maxima/minima, and end behavior determined by degree and leading coefficient.

1. 
Polynomials
Unit 6

2. What is a polynomial?
 An expression with two or more algebraic terms.
 Terms are separated by +/-
 Common Terms:
 Monomial
 An expression with exactly one algebraic term
 Binomial
 Trinomial
 Standard form: When a polynomial is written in
descending order of exponents

3. Naming Polynomials
 Polynomials are named based on their degree and
number of terms.
 Degree of a Monomial: The sum of the exponents
of the variables in that term
 Degree of a Polynomial (with one variable): The
highest degree of its terms (the highest exponent)
 Leading Coefficient: Coefficient of term with the
highest degree

4. Naming Polynomials (cont.)
Degree Name Example
0
1
2
3
4
5
6 or more…

5. General Shape of Polynomial Graphs
Constant Linear

6. General Shape of Polynomial Graphs
Quadratic Cubic

7. General Shape of Polynomial Graphs
Quartic Quintic

8. Important Info for Polynomial Graphs
 x-intercept
 Where the graph crosses
the x-axis
 y-intercept
 Where the graph crosses
the y-axis
 If the polynomial is a
function, there will only be
ONE y-intercept
 Why?

9. Important Info for Polynomial Graphs
 Increasing
 A function is increasing on
an interval if the y-value
increases as the x-value
increases
 AKA, as you travel from left
to right, graph goes up
 Decreasing
 A function is decreasing on
an interval if the y-value
decreases as the x-value
increases
 AKA, as you travel from left
to right, graph goes down

10. Important Info for Polynomial Graphs
 Relative Minimum
 The y-value of the lowest
point of a particular region
of the graph
 Relative Maximum
 The y-value of the highest
point of a particular region
of the graph

11. Important Info for Polynomial Graphs
 Roots, Zeros, Solutions
 All refer to same points on
the graph
 Same as x-intercepts
 Where the graph crosses
the x-axis

12. End Behavior of a Polynomial Graph
 The behavior of the graph of a function f(x) as x
approaches positive or negative infinity
 AKA, what directions will the arrows be pointing
 The degree and leading coefficient determine the
end behavior of the polynomial
 Even Degree – arrows point same direction
 Odd Degree – arrows point different directions
 Positive LC – right arrow will point up
 Negative LC – right arrow will point down

13. End Behavior Chart
Degree Leading
Coefficent
End Behavior Shortcut
Notation
Even Positive
Even Negative
Odd Positive
Odd Negative