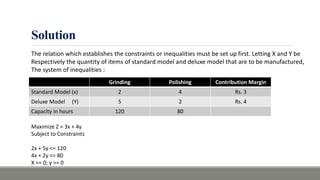
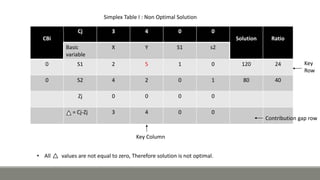
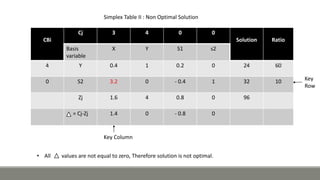
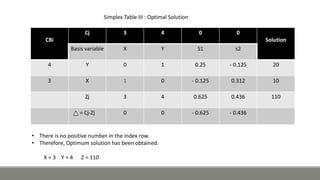
The document discusses using the simplex method to solve a linear programming problem. It provides an example problem that involves maximizing profits from manufacturing two product types with limited resources. The simplex method is used to iteratively solve the problem by setting up a simplex table, identifying key columns and rows, and updating values until an optimal solution is reached. The optimal solution found was for 3 units of the standard model and 4 units of the deluxe model, providing maximum profits of 110.

1. Subject –
Operations Research
Topic –
Simplex Method(Problem)
Class –
FY MMS
Presented By-
Taslima Bashir Mujawar

2. Why we use Simplex Method ?
 The graphical method is not applicable to Linear Programming
Problems with more than two variables. Therefore, Simplex Method
is used to give the optimal solution.
The graphical method is applicable only when-
2x + 3y <= 20

3. Simplex Method
Simplex Method is considered as one of the basic techniques from
which many linear programming techniques are derived directly or
indirectly.
The simplex method is an iterative, stepwise process which
approaches an optimum solution in order to reach an objective
function of maximization or minimization.

4. Important Condition
For Maximization Case :
= Cj – Zj <= 0 …[ 0 or negative no.]
For Minimization Case :
= Cj – Zj >= 0 …[ 0 or positive no.]

5. Example
A mechanic shop manufactures two models, standard and deluxe.
Each standard model requires two hours of grinding and four hours of
polishing; each deluxe model requires five hours of grinding and two
hours of polishing. The manufacturer has three grinders and two
polishers. Therefore, in 40 hours of week, there are 120 hours of
grinding capacity and 80 hours of polishing capacity. There is
contribution margin of Rs. 3 on each standard model and Rs. 4 on
each deluxe model.

6. Solution
Grinding Polishing Contribution Margin
Standard Model (x) 2 4 Rs. 3
Deluxe Model (Y) 5 2 Rs. 4
Capacity in hours 120 80
Maximize Z = 3x + 4y
Subject to Constraints
2x + 5y <= 120
4x + 2y <= 80
X >= 0; y >= 0
The relation which establishes the constraints or inequalities must be set up first. Letting X and Y be
Respectively the quantity of items of standard model and deluxe model that are to be manufactured,
The system of inequalities :

7. To convert it into an equation, we add a slack variables s1, s2 on the left hand side to get
2x + 5y + s1 = 120
4x + 2y + s2 = 80
The use of slack variables involves the addition of an arbitrary variable to one
side of inequality, transforming it into equality. This arbitrary variable is called
slack variable, since it takes up the slack in the inequality.
The problem can now be expressed as follows:
Max Z = 3x + 4y + 0s1 + 0s2
Subject to constraints,
2x + 5y + s1 + 0s2 = 120
4x + 2y + 0s1 + s2 = 80

8. CBi
Cj 3 4 0 0
Solution Ratio
Basic
variable
X Y S1 s2
0 S1 2 5 1 0 120 24
0 S2 4 2 0 1 80 40
Zj 0 0 0 0
= Cj-Zj 3 4 0 0
Key Column
Key
Row
Contribution gap row
Simplex Table I : Non Optimal Solution
• All values are not equal to zero, Therefore solution is not optimal.

9. New value = Old Value – Corresponding key column value * Corresponding key row value
Key number
For S2,
1) 4 – 2 * 2 / 5 = 3.2
2) 2 – 2 * 5 / 5 = 0
3) 0 – 2 * 1 / 5 = 0.4
4) 1 – 2 * 0 / 5 = 1
5) 80 – 120 * 2 / 5 = 32
Zj ,
1) 4 * 0.4 + 3.2 * 0 = 16
2) 4 * 1 + 0 = 4
3) 4 * 0.2 + 0 = 0.8
4) 4 * 0 + 0 * 1 = 0
5) 24 * 4 + 0 = 96
Zj = (CBi)(Caij)
i = 1
n = 2

10. CBi
Cj 3 4 0 0
Solution Ratio
Basis
variable
X Y S1 s2
4 Y 0.4 1 0.2 0 24 60
0 S2 3.2 0 - 0.4 1 32 10
Zj 1.6 4 0.8 0 96
= Cj-Zj 1.4 0 - 0.8 0
Simplex Table II : Non Optimal Solution
Key Column
Key
Row
• All values are not equal to zero, Therefore solution is not optimal.

11. New value = Old Value – Corresponding key column value * Corresponding key row value
Key number
For y,
1) 0.4 – 0.4 * 3.2 / 3.2 = 0
2) 1 – 0.4 * 0 / 3.2 = 1
3) 0.2 – 0.4 * (- 0.4) / 3.2 = 0.25
4) 0 – 0.4 * 1 / 3.2 = -0.125
5) 24 – 0.4 * 32 /3.2 = 20
Zj ,
1) 0 + 3* 1 = 3
2) 4 * 1 + 3* 0 =4
3) 4 * 0.25 + 3 * ( -0.125) = 0.625
4) 4 * (- 0.125) + 3 * 0.312 = 0.436
5) 4 * 20 + 3 * 10 = 110
Zj = (CBi)(Caij)
i = 1
n = 2

12. CBi
Cj 3 4 0 0
Solution
Basis variable X Y S1 s2
4 Y 0 1 0.25 - 0.125 20
3 X 1 0 - 0.125 0.312 10
Zj 3 4 0.625 0.436 110
= Cj-Zj 0 0 - 0.625 - 0.436
Simplex Table III : Optimal Solution
• There is no positive number in the index row.
• Therefore, Optimum solution has been obtained.
X = 3 Y = 4 Z = 110

14. Any Queries…??