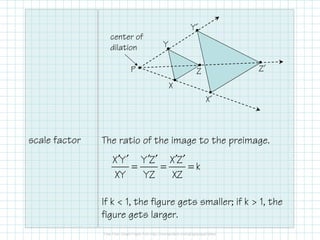
The document defines and provides examples of dilations. A dilation is a transformation that changes the size of a figure but not its shape. It is defined by a center of dilation and a scale factor. The scale factor is the ratio of the length of an image to the corresponding preimage. A scale factor greater than 1 results in an enlarged figure, while a scale factor between 0 and 1 results in a smaller figure. The document provides examples of identifying the scale factor of a dilation and calculating the new coordinates of dilated points and figures.

1. Obj. 38 Dilations
The student is able to (I can):
• Identify and draw dilations

2. dilation
A transformation that changes the size of
a figure but not the shape.
Example:
Tell whether each transformation appears
to be a dilation.
1.
2.
S
yes
S
no

3. center of
dilation
Y´
•
Y•
•
•
P
Z´
Z
X
•
•
X´
scale factor
The ratio of the image to the preimage.
X′Y ′ Y ′Z′ X′Z′
=
=
=k
XY
YZ
XZ
If k < 1, the figure gets smaller; if k > 1, the
figure gets larger.

4. Example
1. What is the scale factor of the dilation?
5
10
12
24
5 1
12 1
k=
= (or k =
= )
10 2
24 2
2. If you are enlarging a 4x6 photo by a
scale factor of 4, what are the new
dimensions?
4(4) = 16
6(4) = 24
New dimensions = 16x24

5. Scale factor and coordinates:
|
-4
B
•
|
-2
|
C
•
|
|
0
|
A
•
|
2
|
D
•
|
4
What point is the image of A under the
dilation with the given scale factor with the
center of dilation at 0?
1. k = 2
2(2) = 4, thus point D
2. k = -1
3. k = −
1
2
2(-1) = -2, thus point B
 − 1  = −1, thus point C
2

2


6. If P(x, y) is a point being dilated centered
at the origin, with a scale factor of k, then
the image of the point is P´(kx, ky).
Example: What are the coordinates of a
triangle with vertices S(-3, 2), K(0, 4), and
Y(2, -3) under a dilation with a scale factor
of 3, centered at the origin?
S´(3(-3), 3(2)) = S´(-9, 6)
K´(3(0), 3(4)) = K´(0, 12)
Y´(3(2), 3(-3)) = Y´(6, -9)
Note: If k is negative, the resulting dilation
will be rotated 180º about the center.

7. Examples
Dilate the following vertices by the given
scale factor. All dilations are centered
about the origin.
1. B(2, 0), I(3, 3), G(5, -1); k=2
B´(4, 0), I´(6, 6), G´(10, -2)
1
2. T(-3, -3), I(-3, 3), N(6, 3), Y(6, -3); k=
3
T´(-1, -1), I´(-1, 1), N´(2, 1), Y´(2, -1)
1
3. S(-4, 2), E(-6, 0), A(-2, -4); k= −
2
S´(2, -1), E´(3, 0), A´(1, 2)