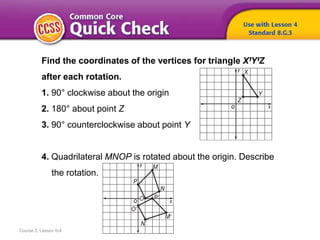
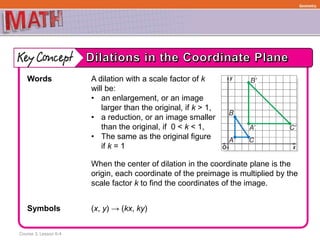
This document discusses how to find the coordinates of vertices for a triangle after various rotations and describes a quadrilateral being rotated about the origin. It provides examples of finding coordinates after a 90° clockwise rotation, 180° rotation about a point Z, 90° counterclockwise rotation about a point Y. It also discusses dilating figures using scale factors and providing examples of dilating triangles and finding the scale factor of a dilation based on diameters.

1. Course 3, Lesson 6-4
Find the coordinates of the vertices for triangle XꞋYꞋZ
after each rotation.
1. 90° clockwise about the origin
2. 180° about point Z
3. 90° counterclockwise about point Y
4. Quadrilateral MNOP is rotated about the origin. Describe
the rotation.

2. Course 3, Lesson 6-4
ANSWERS
1. XꞋ(1, −1), YꞋ (−1, 1), ZꞋ (4, −1)
2. XꞋ (1, −2), YꞋ (1, −3), ZꞋ (1, 1)
3. XꞋ (0, −1), YꞋ (3, 1), ZꞋ (3, −1)
4. 90° clockwise

3. HOW can we best show or describe the
change in position of a figure?
Geometry
Course 3, Lesson 6-4

4. Course 3, Lesson 6-4 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices
and Council of Chief State School Officers. All rights reserved.
Geometry
• 8.G.3
Describe the effect of dilations, translations, rotations, and
reflections on two-dimensional figures using coordinates.
Mathematical Practices
1 Make sense of problems and persevere in solving them.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.

5. To
• dilate a figure with a scale factor of k
on the coordinate plane
• find the scale factor of a dilation of a
figure
Course 3, Lesson 6-4
Geometry

6. Symbols
• (x, y)  (kx, ky)
Course 3, Lesson 6-4
Geometry

7. Course 3, Lesson 6-4
Geometry
Words A dilation with a scale factor of k
will be:
• an enlargement, or an image
larger than the original, if k > 1,
• a reduction, or an image smaller
than the original, if 0 < k < 1,
• The same as the original figure
if k = 1
When the center of dilation in the coordinate plane is the
origin, each coordinate of the preimage is multiplied by the
scale factor k to find the coordinates of the image.
Symbols (x, y) → (kx, ky)

8. 1
Need Another Example?
2
3
Step-by-Step Example
1. A triangle has vertices A(0, 0), B(8, 0), and C(3, –2).
Find the coordinates of the triangle after a dilation
with a scale factor of 4.
The dilation is (x, y) → (4x, 4y). Multiply
the coordinates of each vertex by 4.
So, the coordinates after the dilation are
A'(0, 0), B'(32, 0), and C'(12, –8).
A(0, 0) → (4 • 0, 4 • 0) → (0, 0)
B(8, 0) → (4 • 8, 4 • 0) → (32, 0)
C(3, –2) → [4 • 3, 4 • (–2)] → (12, –8)

9. Answer
Need Another Example?
A triangle has vertices D(1, 2), E(0, 4), and
F(1, –1). Find the coordinates of the triangle
after a dilation with a scale factor of 3.
D'(3, 6), E'(0, 12), F'(3, –3)

10. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
2. A figure has vertices J(3, 8), K(10, 6), and L(8, 2).
Graph the figure and the image of the figure after a dilation
with a scale factor of .
The dilation is (x, y) → x, y .
Multiply the coordinates of each
vertex by . Then graph both figures
on the coordinate plane.
Check
J(3, 8) → →
K(10, 6) → → K'(5, 3)
L(8, 2) → → L'(4, 1)
J
K
L
J'
K'
L'
Draw lines through the origin and each of the
vertices of the original figure. The vertices of
the dilation should lie on those same lines.

11. Answer
Need Another Example?
A figure has vertices H(–8, 4), J(6, 4), K(6, –4), and
L(–8, –4). Graph the figure and the image of the
figure after a dilation with a scale factor of .

12. 1
Need Another Example?
2
3
4
Step-by-Step Example
3. Through a microscope, the image of a grain of sand with a
0.25-millimeter diameter appears to have a diameter of
11.25 millimeters. What is the scale factor of the dilation?
Write a ratio comparing the diameters of the two images.
=
So, the scale factor of the dilation is 45.
= 45

13. Answer
Need Another Example?
The pupil of Josh’s eye is 6 millimeters in
diameter. His doctor uses medicine to dilate his
pupils so that they are 9 millimeters in diameter.
What is the scale factor of the dilation?

14. How did what you learned
today help you answer the
HOW can we best show or describe the
change in position of a figure?
Course 3, Lesson 6-4
Geometry

15. How did what you learned
today help you answer the
HOW can we best show or describe the
change in position of a figure?
Course 3, Lesson 6-4
Geometry
Sample answers:
• You can use symbolic notation (x, y) →(kx , ky) to
describe the dilations of a figure with a scale factor.
• You can graph the original figure and the image to
show the figure after a dilation with a scale factor of k.

16. If the scale factor of
a dilation is ,
is the dilation an
enlargement or
a reduction?
Course 3, Lesson 6-4
Ratios and Proportional RelationshipsFunctionsGeometry
3
2