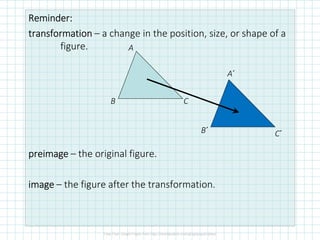
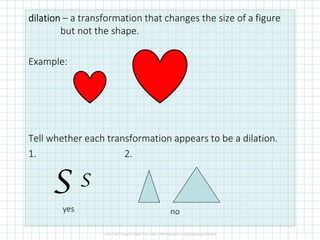
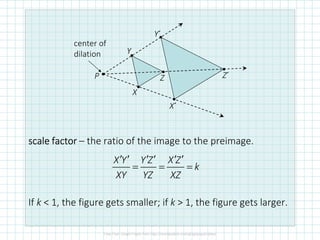
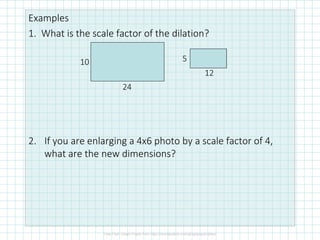
The document covers concepts of dilation, scale factors, ratios, and proportions in mathematics. It defines transformations, particularly dilations that change size but not shape, and explains how to identify and solve problems using these concepts. Examples are provided to illustrate how to calculate scale factors, solve proportions, and determine angles based on ratios.

1. Dilation, Scale Factor, & Proportion
The student is able to (I can):
• Identify dilations
• Identify scale factors and use scale factors to solve
problems
• Write and simplify ratios
• Use proportions to solve problems

2. Reminder:Reminder:Reminder:Reminder:
transformationtransformationtransformationtransformation – a change in the position, size, or shape of a
figure.
preimagepreimagepreimagepreimage – the original figure.
imageimageimageimage – the figure after the transformation.
A
B C
A´´´´
B´´´´ C´´´´

3. dilationdilationdilationdilation – a transformation that changes the size of a figure
but not the shape.
Example:
Tell whether each transformation appears to be a dilation.
1. 2.
SS
yes no

4. ratioratioratioratio – a comparison of two numbers by division.
The ratio of two numbers a and b, where b does not equal 0
(b ≠ 0) can be written as
a to b
a : b
Example: The ratio comparing 1 and 2 can be written 1 to 2,
1 : 2, or .
To compare more than two numbers, use “dot”
notation. Ex. 3 : 7 : 9
a
b
1
2

5. proportionproportionproportionproportion – an equation stating that two ratios are equal.
Two sets of numbers are proportionalproportionalproportionalproportional if they use the same
ratio.
Example: or a : b = c : d
Cross Products Property
In a proportion, if , and b and d ≠ 0, then ad = bc
=
a c
b d
a c
b d
=

6. scalescalescalescale factorfactorfactorfactor – the ratio of the image to the preimage.
If k < 1, the figure gets smaller; if k > 1, the figure gets larger.
•
•
•
X´´´´
Y´´´´
Z´´´´
•
•
•
P
X
Y
Z
center of
dilation
X Y Y Z X Z
k
XY YZ XZ
′ ′ ′ ′ ′ ′
= = =

7. Examples
1. What is the scale factor of the dilation?
2. If you are enlarging a 4x6 photo by a scale factor of 4,
what are the new dimensions?
10
24
5
12

8. Examples
1. What is the scale factor of the dilation?
2. If you are enlarging a 4x6 photo by a scale factor of 4,
what are the new dimensions?
4(4) = 16 6(4) = 24
New dimensions = 16x24
10
24
5
12
5 1 12 1
(or )
10 2 24 2
k k= = = =

9. Examples Solve each proportion:
1.
2.
3.
3
8 32
x
=
4 2
5x
=
2
6 3
x x −
=

10. Examples Solve each proportion:
1.
8x = 96 x = 12
2.
2x = 20 x = 10
3.
3x = 6(x – 2)
3x = 6x – 12
–3x = –12 x = 4
3
8 32
x
=
4 2
5x
=
2
6 3
x x −
=

11. Examples 4. The ratio of the angles of a triangle is
2: 2: 5. What is the measure of each
angle?

12. Examples 4. The ratio of the angles of a triangle is
2: 2: 5. What is the measure of each
angle?
2x + 2x + 5x = 180˚
9x = 180˚
x = 20
2(20) = 40˚
2(20) = 40˚
5(20) = 100˚