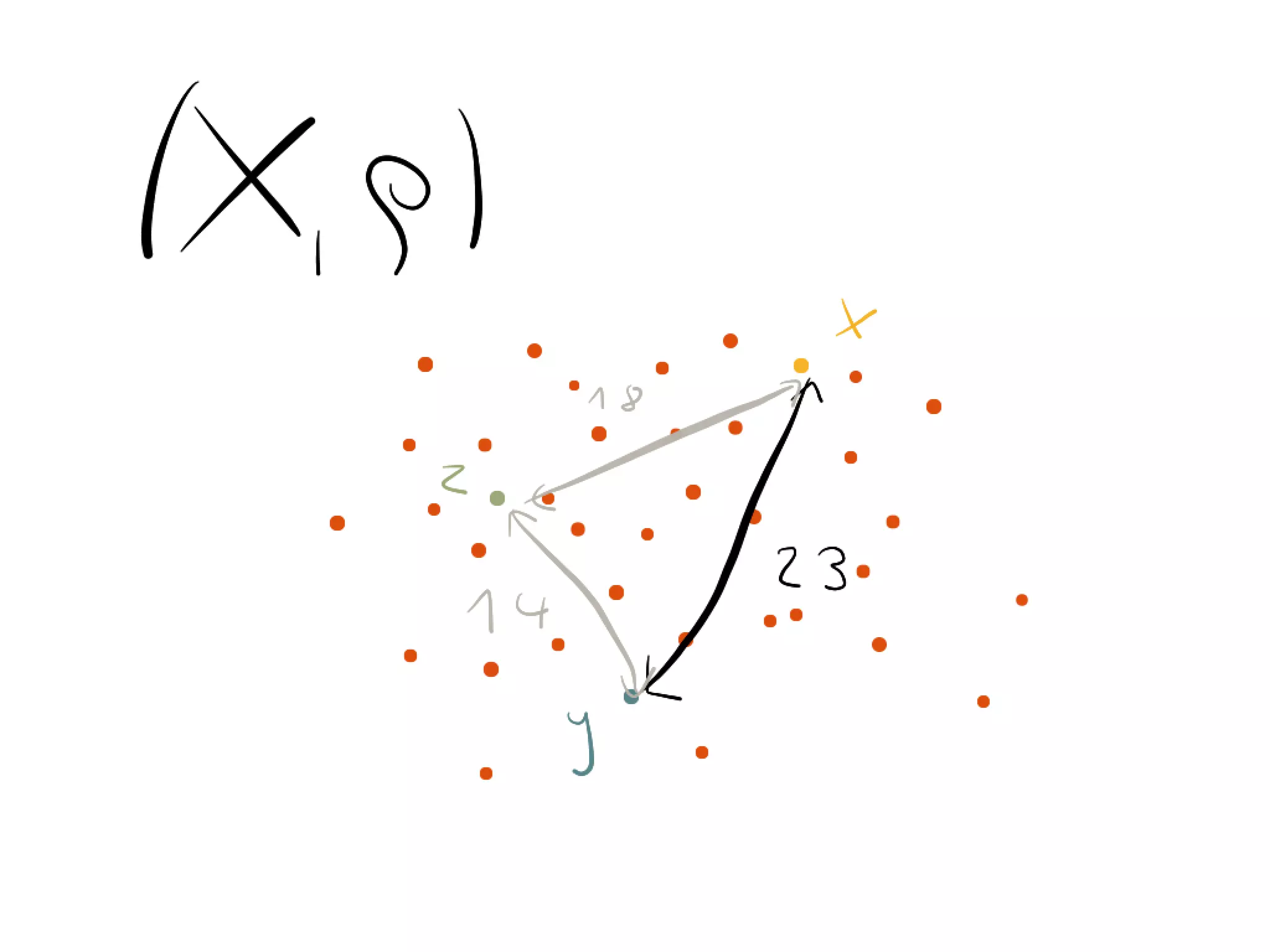
The document discusses convergence in sequential spaces and uniformly sequential spaces. It defines continuous and uniformly continuous mappings between such spaces, and proves some equivalent properties. It also provides an example of an infinite family of almost disjoint subsets to illustrate these concepts cannot be reversed. The example constructs a family using preimages of convergent rational sequences for irrational numbers.

1. Tancuj, tancuj, konverguj
Jako v konvergenci i v tanci nezáleží na pár prvních
krocích, ale jak tancujete ke konci a kam dotancujete.
Photo by tyle_r on Flickr

4. Které vlastnosti
jdou vyjádřit
konvergencí

5. Které vlastnosti
jdou vyjádřit •Kompaktnost
konvergencí •Úplnost
•Totální omezenost
•Omezenost
•Otevřenost
•Spojitost
• Stejnoměrná spojitost
• Souvislost
• Separabilnost

7. 1. Uzavřenost na podposloupnosti
2. Jednoznačnost limity
3. Posloupnost nekonvergující k x obsahuje
podposloupnost, která je “daleko od x”.
4. Konvergence konstantní posloupnosti

10. Topologie

11. •Kompaktnost
•Úplnost
•Totální omezenost
•Omezenost
•Otevřenost
•Spojitost
•Stejnoměrná spojitost
•Souvislost
•Separabilnost

13. 1. Podposloupnosti blízkých jsou blízké
2. Různé konstantní nejsou blízké
3. Neblízké posloupnosti obsahují
podposloupnosti, které jsou
“daleko od sebe”.

15. Cauchyovská posloupnost

16. Kam jsme dotancovali
Dirty Dancing (1987)

17. •Kompaktnost
•Úplnost
•Totální omezenost
•Omezenost
•Otevřenost
•Spojitost
•Stejnoměrná spojitost
•Souvislost
•Separabilnost

18. The following theorem is often covered in basic course of mathematic
lysis. We include it for completeness.
3. Properties defined by
convergence
Theorem 3.2. Let ⌅X and ⌅Y be two sequential structures generated by
In this chapter we will use the following convention: when we say a uniformly
sequential space (X, ⇠) has a property defined for a sequential space we mean
that ⌅⇠ has this property.
spaces (X, %) and (Y, ). Let f : X ! Y be a mapping. Then the follow
3.1 Continuous and uniformly continuous map-
pings
equivalent:
Definition 3.1. Let ⌅X and ⌅Y be two sequential structures on sets X and Y .
We say f : X ! Y is a continuous mapping ⌅X to ⌅Y if ({xn }, x) 2 ⌅X implies
that ({f (xn )}, f (x)) 2 ⌅Y .
The following theorem is often covered in basic course of mathematical ana-
lysis. We include it for completeness.
(i) f : (X, %) ! (Y, ) is continuous;
Theorem 3.2. Let ⌅X and ⌅Y be two sequential structures generated by metric
spaces (X, %) and (Y, ). Let f : X ! Y be a mapping. Then the following are
equivalent:
(i) f : (X, %) ! (Y, ) is continuous;
(ii) f : ⌅X ! ⌅Y is continuous.
(ii) f : ⌅X ! ⌅Y is continuous.
Proof. Let x 2 X be a fixed point.
Let condition (i) hold and xn ! x (that is, ({xn }, x) 2 ⌅X ). For " > 0 we
find > 0 from Definition 1.6. Then there exists n" such that for 8n n" we
have %(xn , x) < and then (f (xn ), f (x)) < ". Hence f (xn ) ! f (x) in Y , that
is, ({f (xn )}, f (x)) 2 ⌅Y .
Let now condition (ii) hold and for contradiction suppose that (i) does not.
Then
Proof. Let x 2 X be a fixed point.
9" > 0 8 > 0 8y 2 X : %(x, y) < ) (f (x), f (y)) ".
We fix this " and find a sequence {xn } such that %(x1 , x) < 1 and %(xn+1 , x) <
min( n , %(xn , x)) for n 2 N. Then xn ! x hence from (ii) f (xn ) ! f (x). This is
1
not possible since (f (xn ), f (x)) " for n 2 N.
Let condition (i) hold and xn ! x (that is, ({xn }, x) 2 ⌅X ). For "
Definition 3.3. Let (X, ⇠X ) and (Y, ⇠Y ) be two uniformly sequential spaces.
We say f : X ! Y is a uniformly continuous mapping ⇠X to ⇠Y if {xn } ⇠X {yn }
implies that {f (xn )} ⇠Y {f (yn )}.
find > 0 from Definition 1.6. Then there exists n" such that for 8n
Theorem 3.4. Let ⇠X and ⇠Y be two uniformly sequential structures generated
by metric spaces (X, %) and (Y, ). Let f : X ! Y be a mapping. Then the
following are equivalent:
have %(xn , x) < and then (f (xn ), f (x)) < ". Hence f (xn ) ! f (x) in
(i) f : (X, %) ! (Y, ) is uniformly continuous;
(ii) f : (X, ⇠X ) ! (Y, ⇠Y ) is uniformly continuous.
10
is, ({f (xn )}, f (x)) 2 ⌅Y .
Let now condition (ii) hold and for contradiction suppose that (i) do
Then
9" > 0 8 > 0 8y 2 X : %(x, y) < ) (f (x), f (y)) ".
We fix this " and find a sequence {xn } such that %(x1 , x) < 1 and %(xn+
min( n , %(xn , x)) for n 2 N. Then xn ! x hence from (ii) f (xn ) ! f (x).
1
not possible since (f (xn ), f (x)) " for n 2 N.

19. The following theorem is often covered in basic course of mathematic
lysis. We include it for completeness.
3. Properties defined by
convergence
Theorem 3.2. Let ⌅X and ⌅Y be two sequential structures generated by
In this chapter we will use the following convention: when we say a uniformly
sequential space (X, ⇠) has a property defined for a sequential space we mean
that ⌅⇠ has this property.
spaces (X, %) and (Y, ). Let f : X ! Y be a mapping. Then the follow
3.1 Continuous and uniformly continuous map-
pings
equivalent:
Definition 3.1. Let ⌅X and ⌅Y be two sequential structures on sets X and Y .
We say f : X ! Y is a continuous mapping ⌅X to ⌅Y if ({xn }, x) 2 ⌅X implies
that ({f (xn )}, f (x)) 2 ⌅Y .
The following theorem is often covered in basic course of mathematical ana-
lysis. We include it for completeness.
(i) f : (X, %) ! (Y, ) is continuous;
Theorem 3.2. Let ⌅X and ⌅Y be two sequential structures generated by metric
spaces (X, %) and (Y, ). Let f : X ! Y be a mapping. Then the following are
equivalent:
(i) f : (X, %) ! (Y, ) is continuous;
(ii) f : ⌅X ! ⌅Y is continuous.
(ii) f : ⌅X ! ⌅Y is continuous.
Proof. Let x 2 X be a fixed point.
Let condition (i) hold and xn ! x (that is, ({xn }, x) 2 ⌅X ). For " > 0 we
find > 0 from Definition 1.6. Then there exists n" such that for 8n n" we
have %(xn , x) < and then (f (xn ), f (x)) < ". Hence f (xn ) ! f (x) in Y , that
is, ({f (xn )}, f (x)) 2 ⌅Y .
Let now condition (ii) hold and for contradiction suppose that (i) does not.
Then
Proof. Let x 2 X be a fixed point.
9" > 0 8 > 0 8y 2 X : %(x, y) < ) (f (x), f (y)) ".
We fix this " and find a sequence {xn } such that %(x1 , x) < 1 and %(xn+1 , x) <
min( n , %(xn , x)) for n 2 N. Then xn ! x hence from (ii) f (xn ) ! f (x). This is
1
not possible since (f (xn ), f (x)) " for n 2 N.
Let condition (i) hold and xn ! x (that is, ({xn }, x) 2 ⌅X ). For "
Definition 3.3. Let (X, ⇠X ) and (Y, ⇠Y ) be two uniformly sequential spaces.
We say f : X ! Y is a uniformly continuous mapping ⇠X to ⇠Y if {xn } ⇠X {yn }
implies that {f (xn )} ⇠Y {f (yn )}.
find > 0 from Definition 1.6. Then there exists n" such that for 8n
Theorem 3.4. Let ⇠X and ⇠Y be two uniformly sequential structures generated
by metric spaces (X, %) and (Y, ). Let f : X ! Y be a mapping. Then the
following are equivalent:
have %(xn , x) < and then (f (xn ), f (x)) < ". Hence f (xn ) ! f (x) in
(i) f : (X, %) ! (Y, ) is uniformly continuous;
(ii) f : (X, ⇠X ) ! (Y, ⇠Y ) is uniformly continuous.
10
is, ({f (xn )}, f (x)) 2 ⌅Y .
Let now condition (ii) hold and for contradiction suppose that (i) do
Then ∃
9" > 0 8 > 0 8y 2 X : %(x, y) < ) (f (x), f (y)) ".
We fix this " and find a sequence {xn } such that %(x1 , x) < 1 and %(xn+
min( n , %(xn , x)) for n 2 N. Then xn ! x hence from (ii) f (xn ) ! f (x).
1
not possible since (f (xn ), f (x)) " for n 2 N.

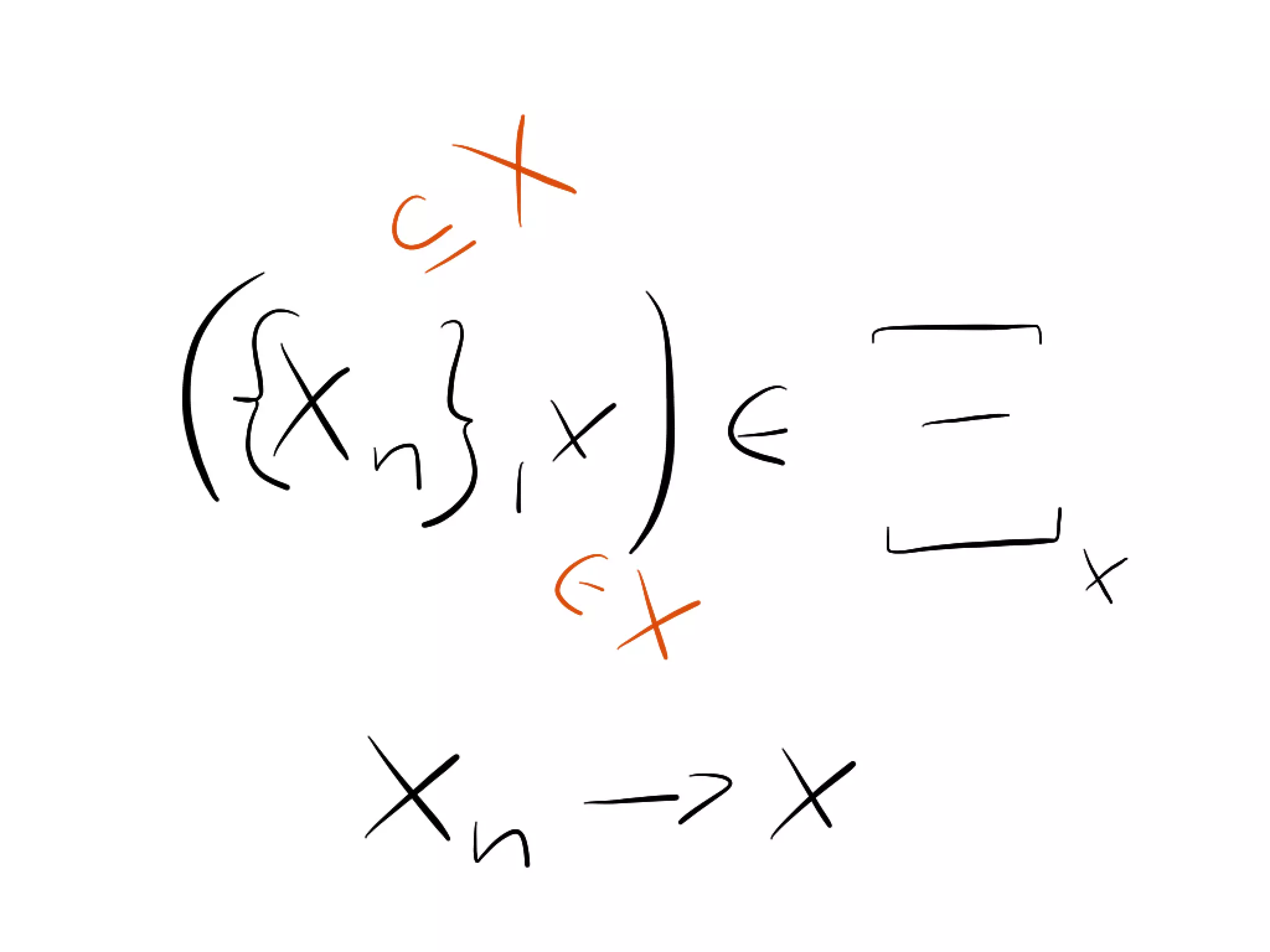
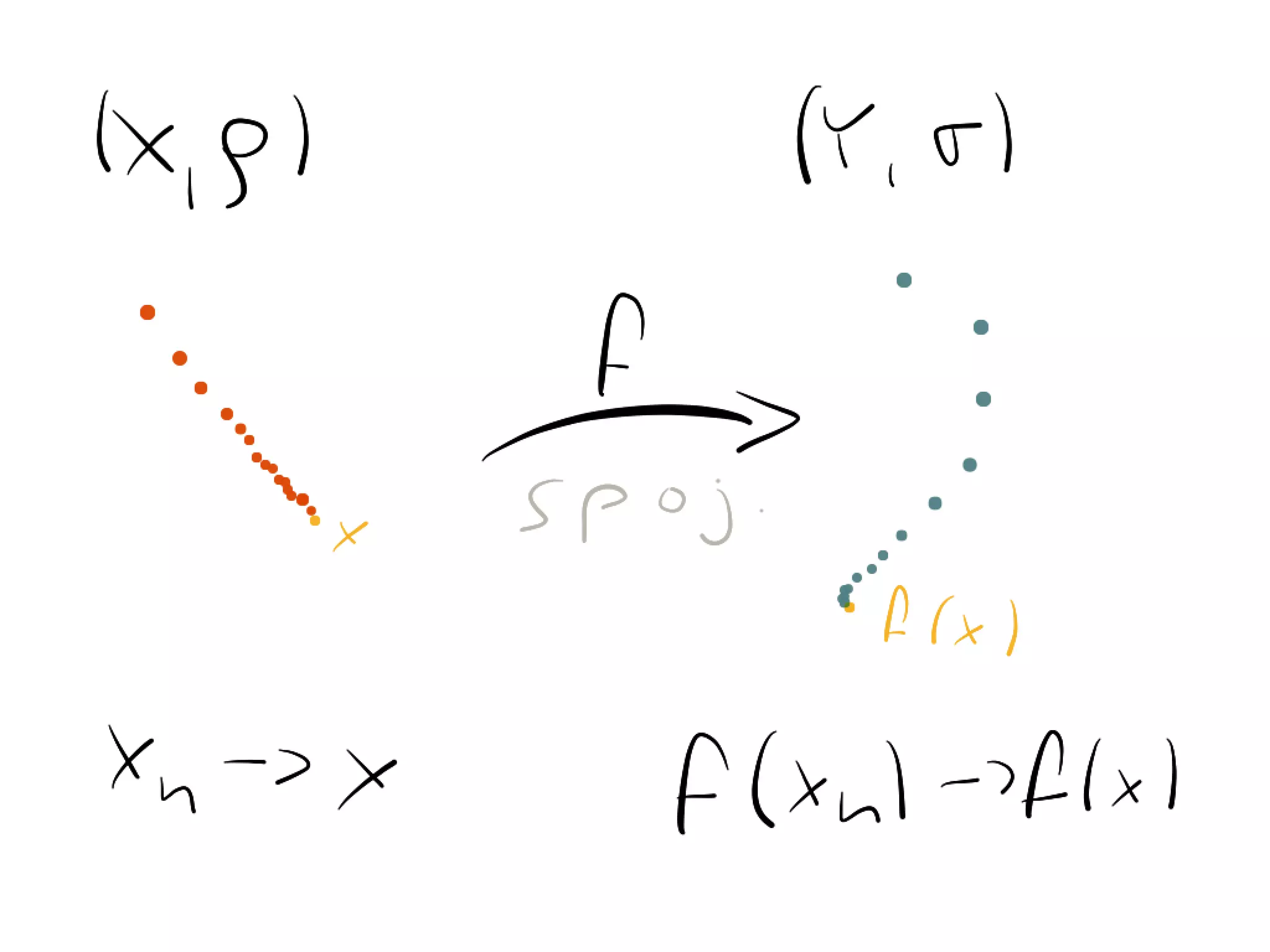
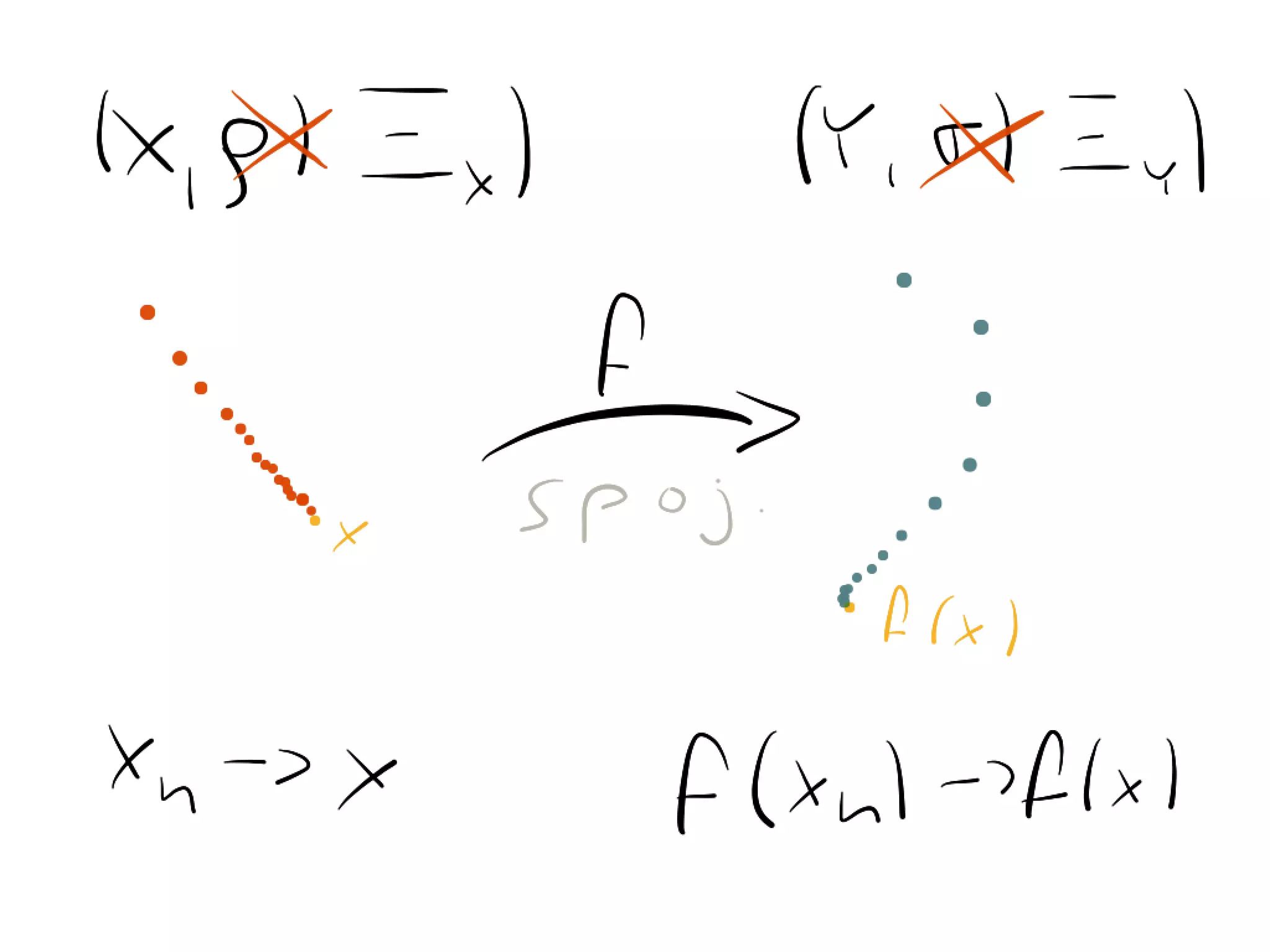
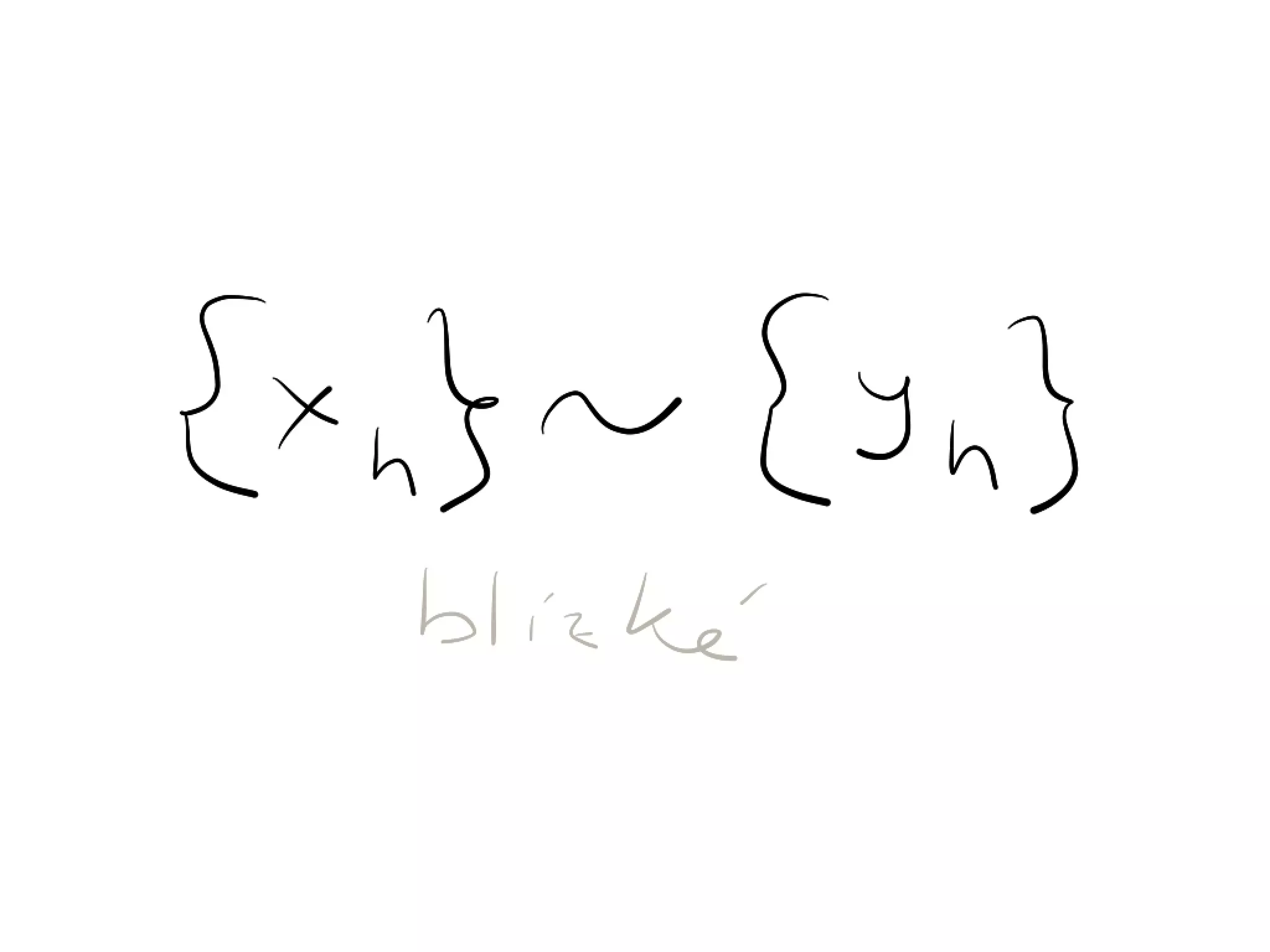
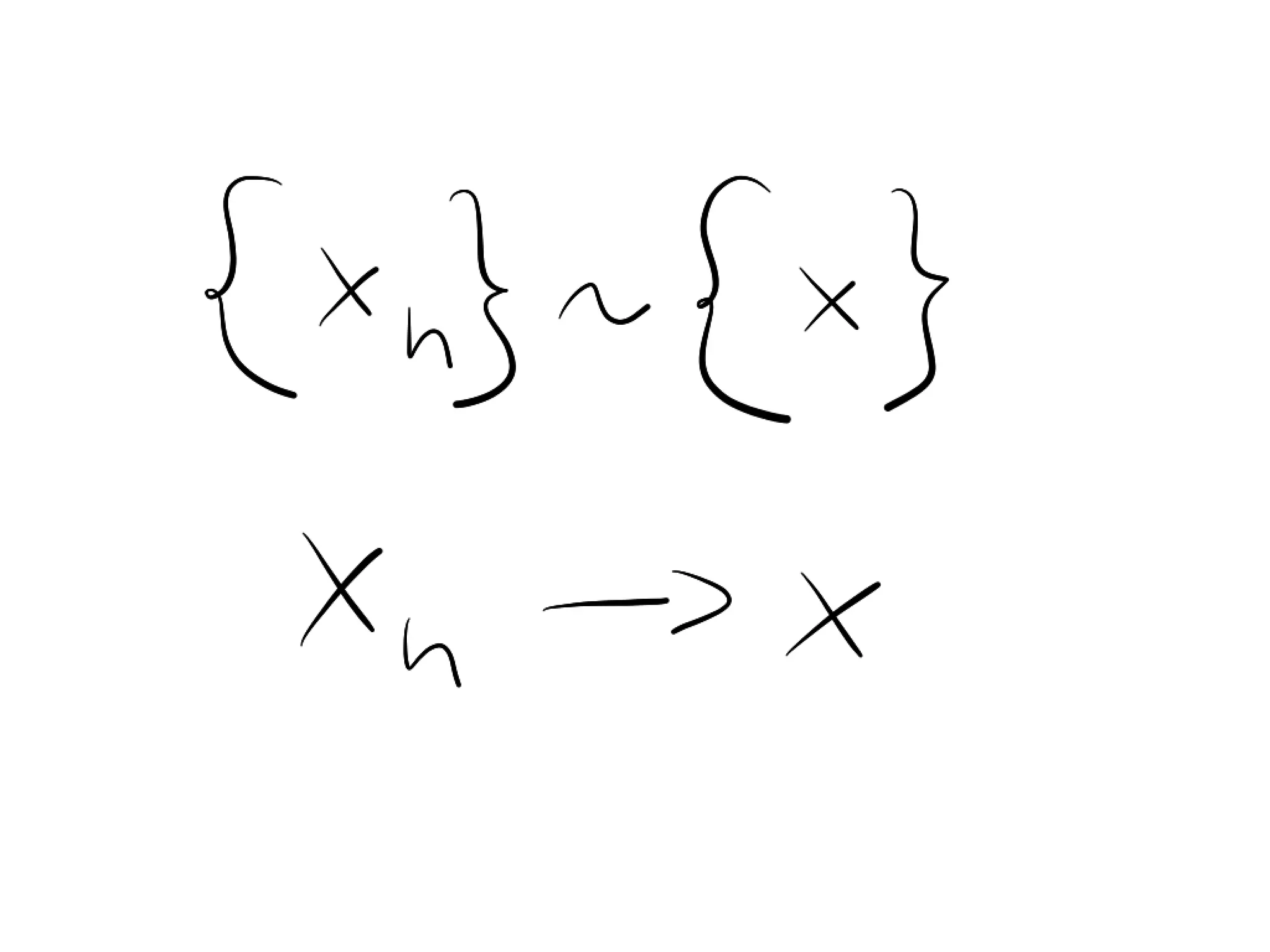
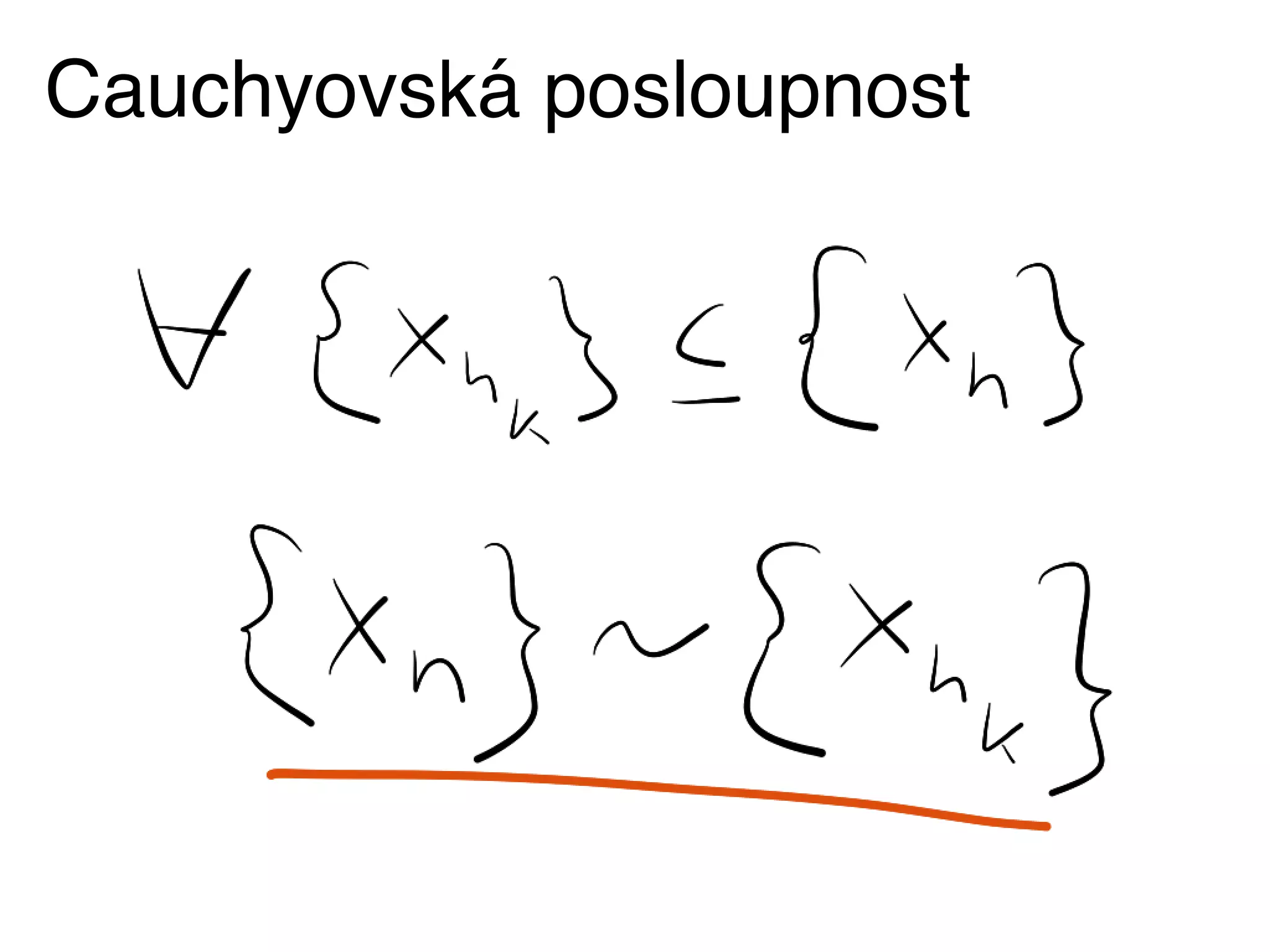
20. Example 3.17. We say two infinite sets are almost disjoint if their inte
is finite. Let us assume an infinite maximal family of almost disjoint su
N and denote it as MAD(N).
Theorem 3.16. Let (X, ⇠X ), (Y, ⇠Y ) be two uniformly sequential spaces, f :
X ! Y be a continuous mapping and (X, ⇠X ) be compact. Then f is uniformly
continuous.
Proof. Let {xn } ⇠X {yn } and let us for contradiction suppose that {f (xn )} 6⇠Y
For a reader’s image of some infinite family of almost disjoint subsets
{f (yn )}. Then from (U3) we find subsequences {f (xnk )} and {f (ynk )} such
that for none their subsequences we have {f (xnki )} ⇠Y {f (ynki )}. Because X
is compact we can find subsequences {xnki } of {xnk }, {ynki } of {ynk } and points
x, y 2 X such that ({xnki }, x) 2 ⌅⇠X and ({ynki }, y) 2 ⌅⇠X . Since {xn } ⇠X {yn }
will show a construction of one. Let f : N ! Q be a bijection of natural n
we have {xnk } ⇠X {ynk } and therefore x = y. Mapping f is continuous so
({f (xnki )}, f (x)) 2 ⌅⇠Y and ({f (ynki )}, f (x)) 2 ⌅⇠Y . That is, {f (xnki )} ⇠Y
{f (x)} and {f (ynki )} ⇠Y {f (x)} which gives us {f (xnki )} ⇠Y {f (ynki )} which is
the contradiction.
onto rational numbers. For every irrational x 2 R Q we will choose one
The following example proves that the implication in the previous theorem
can not be reversed.
Example 3.17. We say two infinite sets are almost disjoint if their intersection
sequence {rn } such that rn ! x. Then Sx := f 1 [{rn }] ⇢ N is a prei
is finite. Let us assume an infinite maximal family of almost disjoint subsets of
N and denote it as MAD(N).
For a reader’s image of some infinite family of almost disjoint subsets of N we
will show a construction of one. Let f : N ! Q be a bijection of natural numbers
that sequence. Then {Sx : x 2 R Q} is an infinite family of almost
onto rational numbers. For every irrational x 2 R Q we will choose one rational
sequence {rn } such that rn ! x. Then Sx := f 1 [{rn }] ⇢ N is a preimage of
that sequence. Then {Sx : x 2 R Q} is an infinite family of almost disjoint
subsets of N because if two sets had an infinite intersection the corresponding
subsets of N because if two sets had an infinite intersection the corres
rational sequences would have an infinite intersection too and since they are both
convergent it follows they would converge to the same point.
Please note that using this construction we do not obtain a MAD(N) as for
example the preimage of the set of all even numbers is almost disjoint with all
constructed sets.
rational sequences would have an infinite intersection too and since they a
We denote MAD(N) = {S↵ : ↵ 2 A} for some set A. Let X := N [ MAD(N)
with the smallest sequential structure such that
S↵ ! {S↵ }, {S↵ } 2 MAD(N).
convergent it follows they would converge to the same point.
This condition can be rephrased: members of S↵ as points in N converge to S↵
as point in MAD(N). Then every continuous mapping to R is bounded but the
space is evidently not compact.
To prove this let f : X ! R be a continuous unbounded mapping. That is,
Please note that using this construction we do not obtain a MAD(N
there exists a sequence {xn } for which f (xn ) ! 1. Now we examine two cases.
First, infinitely many members of {xn } lie in N, so we can find a subsequence
{xnk } ⇢ N. Then there exists S↵ 2 MAD(N) such that {xnk } ! S↵ . Then we
have {f (xnk )} ! f (S↵ ) and {f (xnk )} ! 1 which is a contradiction.
example the preimage of the set of all even numbers is almost disjoint
Second, only finite number of members of {xn } lie in N. Without loss of
generality we suppose that {xn } = {S↵n } ⇢ MAD(N). For every n 2 N we can
find yn 2 N such that |f (yn ) f (S↵n )|  1. The first case yields {f (yn )} is
bounded and so {f (S↵n )} is bounded.
constructed sets. 14
We denote MAD(N) = {S↵ : ↵ 2 A} for some set A. Let X := N [ M
with the smallest sequential structure such that
S↵ ! {S↵ }, {S↵ } 2 MAD(N).
This condition can be rephrased: members of S↵ as points in N converg
as point in MAD(N). Then every continuous mapping to R is bounded