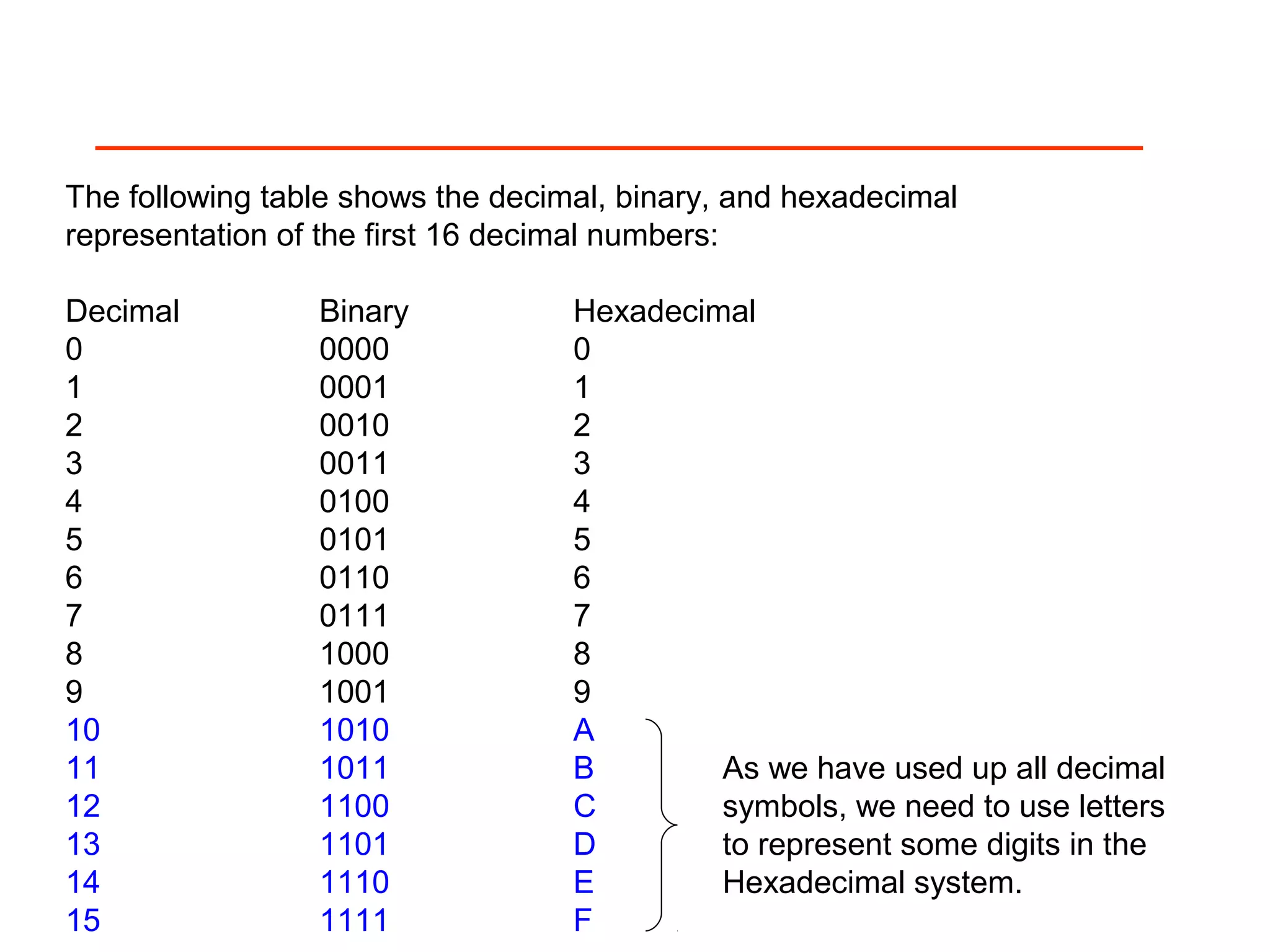
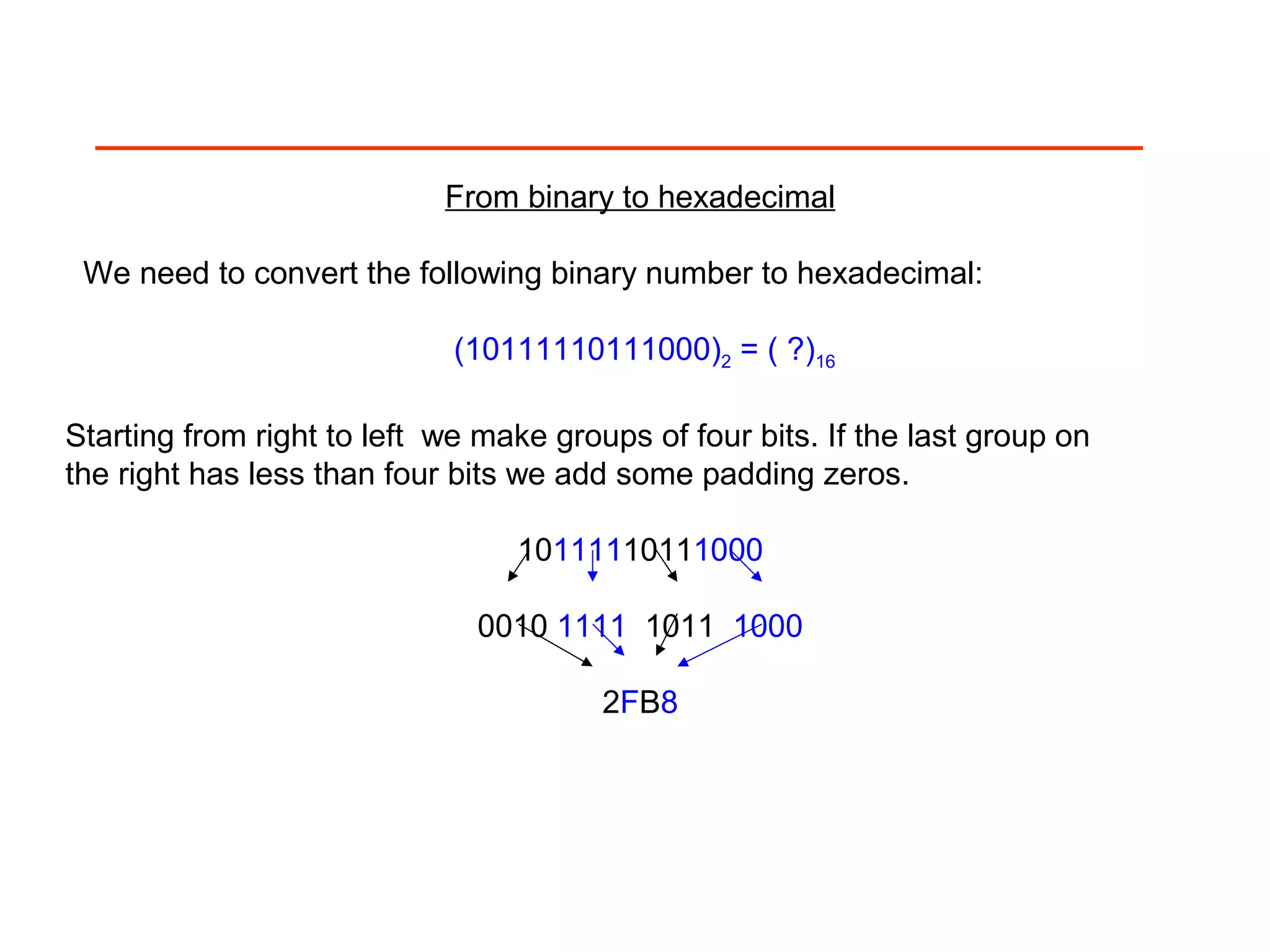
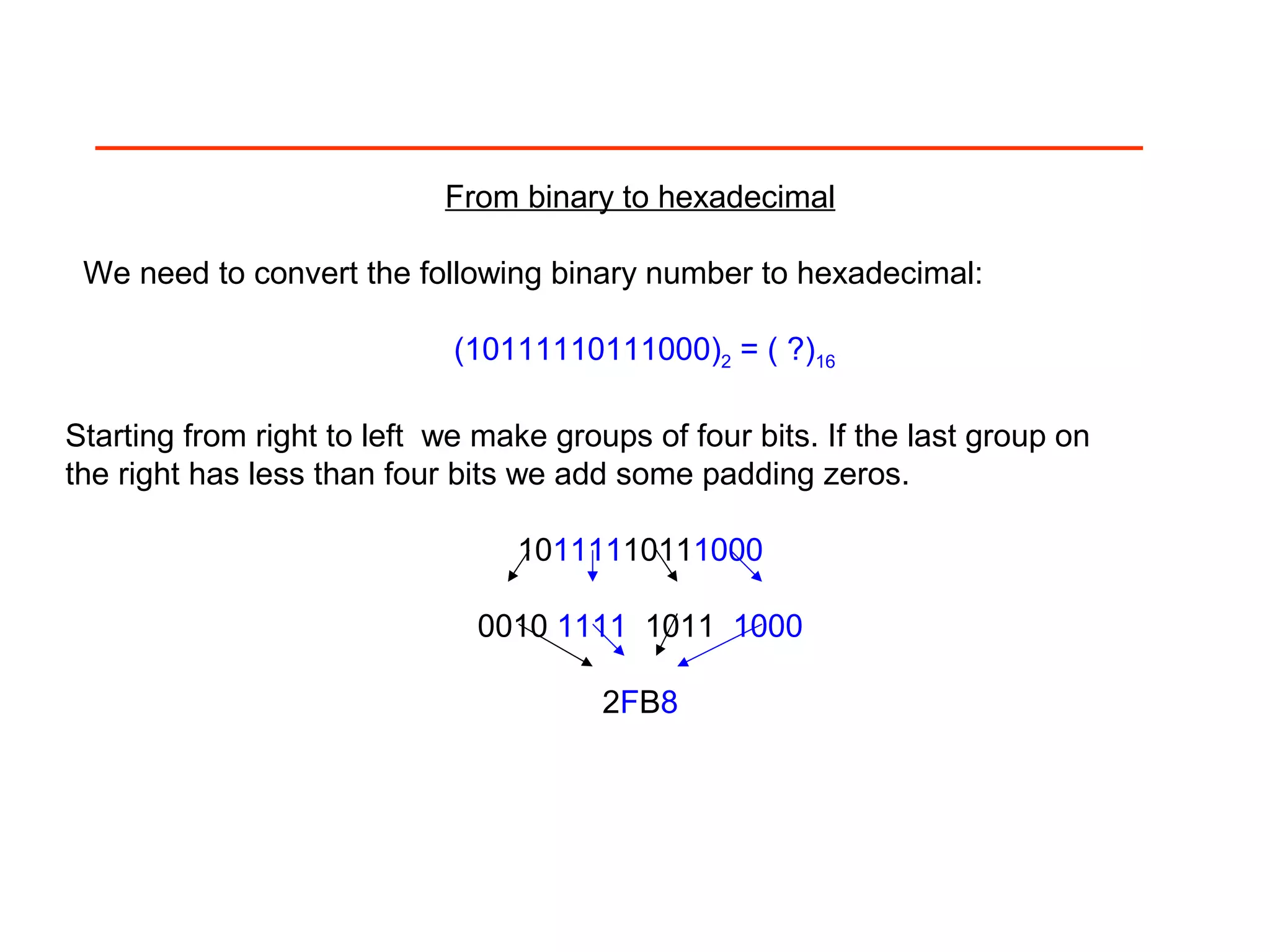
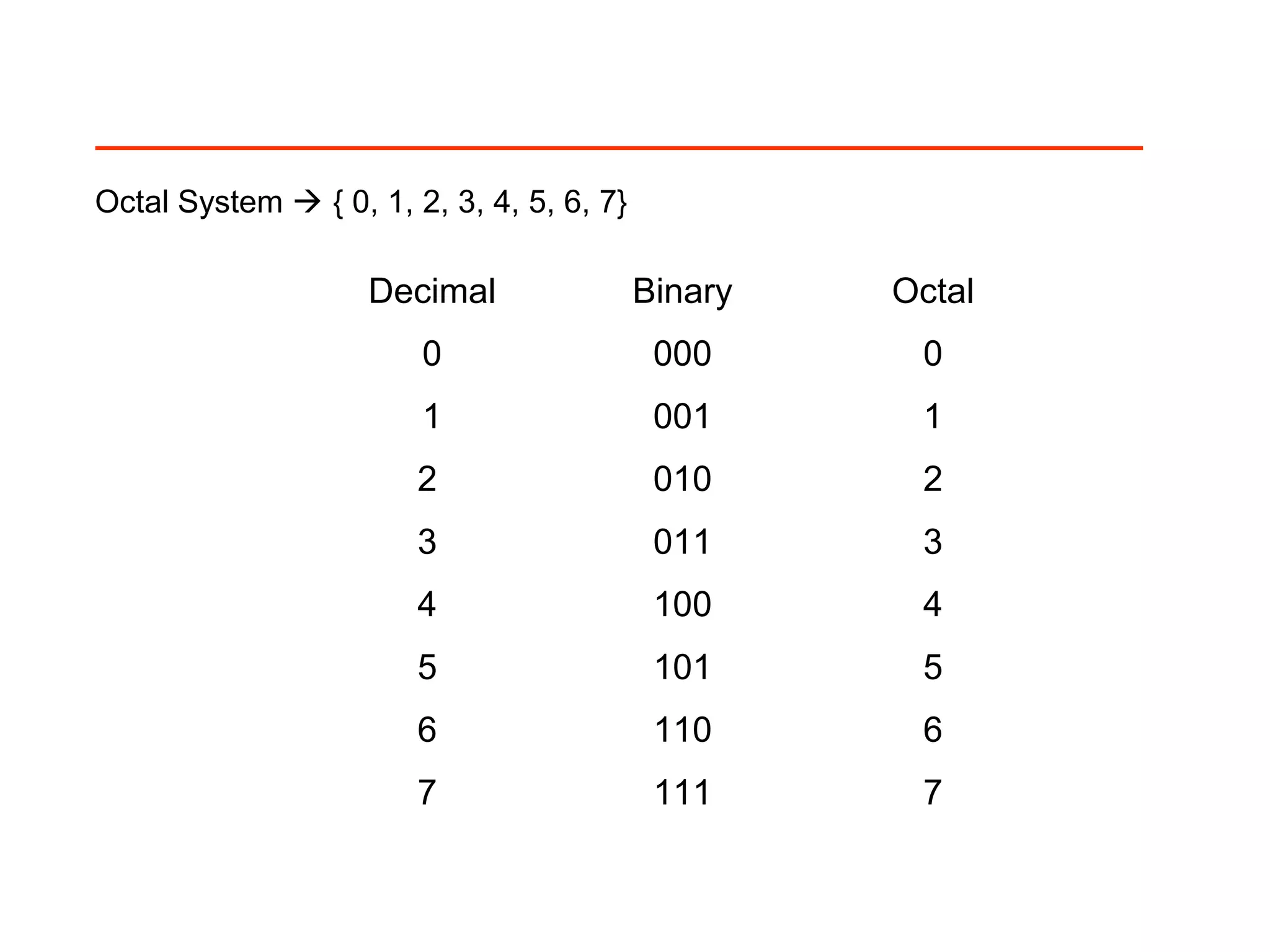
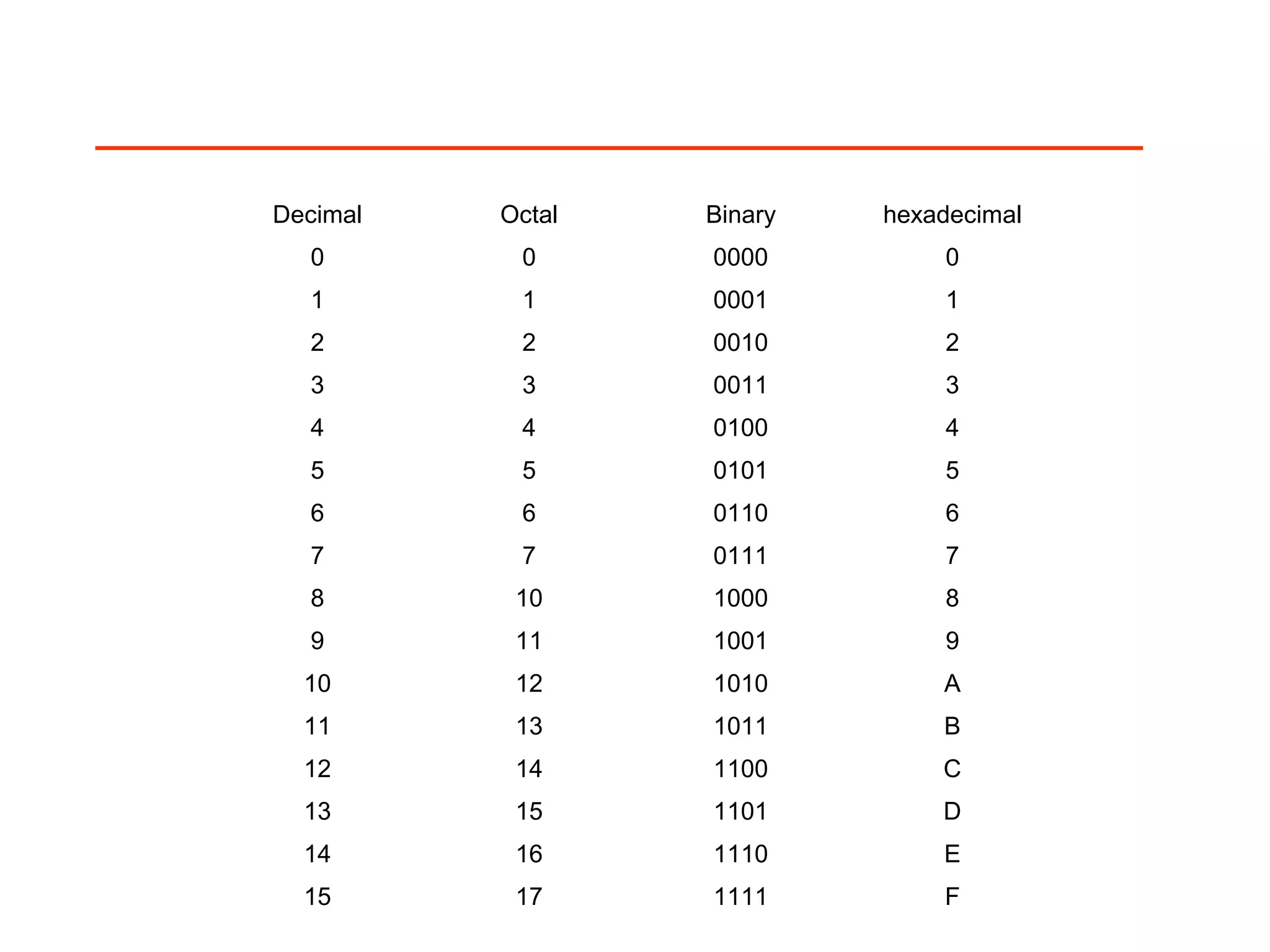
The document discusses positional number systems such as decimal, binary, hexadecimal, and octal. It explains that in a positional number system, the value of a number is determined by the place value of its digits. For example, in the decimal number 325, the 3 is worth 3*100=300, the 2 is worth 2*10=20, and the 5 is worth 5*1=5, so their sum is 325. The document then explains how to convert between decimal, binary, hexadecimal, and octal representations using place value and by grouping binary digits into fixed-width blocks.

1. Presentation By: Shehrevar Davierwala
Visit: http://www.authorstream.com/shehrevard
http://www.slideshare.net/shehrevard
http://sites.google.com/sites/techwizardin
Positional number systems

2. Positional number systems
1.- Decimal number system
2.- Binary number system
3.- Hexadecimal number system
4.- Base conversions

3. Positional number systems
When we need to write the number three hundred and twenty five using decimal
digits we use the following sequence of digits: 325
What do we know about this number?
It is written using decimal digits (a digit from 0 to 9 in decimal notation), which
means that the base of the decimal number system is 10 (the decimal system
has ten symbols or digits).
Formally we can write 325 as:
3 x 102
+ 2 x 101
+ 5 x 100
= (3 x 100) + (2 x 10) + (5 x 1) = 300 + 20 + 5 = 325
Note that 100
= 1

4. Positional number systems
Formally we can write 325 as:
3 x 102
+ 2 x 101
+ 5 x 100
= (3 x 100) + (2 x 10) + (5 x 1) = 300 + 20 + 5 = 325
Note that 100
= 1
By denoting the base of the system as b = 10, we can rewrite 325 as:
325 = 3 x b2
+ 2 x b1
+ 5 x b0
For any number we will refer to each digit by “di”, where “d” represents the digit
and “i” indicates the position in the sequence. Thus we have that any number
can be represented by a sequence of digits: dn dn-1 . . . d2 d1 d0
In our example, d2 = 3, d1 = 2, and d0 = 5

5. Positional number systems
Therefore any number can be represented by a sequence of digits:
dn . . . d2 d1 d0
And its value can be computed as follows:
dn . . . d2 d1 d0 = dn x bn
. . . d2 x b2
+ d1 x b1
+ d0 x b0
Example:
d3 d2 d1 d0
4 7 6 2

6. Positional number systems
Binary numbers can be represented in the same way:
( dn . . . d2 d1 d0 )2 Indicates that the base (b) is binary
And its value can be computed similarly but in this case the base b = 2.
dn . . . d2 d1 d0 = dn x bn
. . . d2 x b2
+ d1 x b1
+ d0 x b0
Example: (10101)2 = 1 x 24
+ 0 x 23
+ 1 x 22
+ 0 x 21
+ 1 x 20
1 x 16 + 0 x 8 + 1 x 4 + 0 x 2 + 1 x 1
16 + 0 + 4 + 0 + 1 = (21)10

7. The following table shows the decimal, binary, and hexadecimal
representation of the first 16 decimal numbers:
Decimal Binary Hexadecimal
0 0000 0
1 0001 1
2 0010 2
3 0011 3
4 0100 4
5 0101 5
6 0110 6
7 0111 7
8 1000 8
9 1001 9
10 1010 A
11 1011 B
12 1100 C
13 1101 D
14 1110 E
15 1111 F
As we have used up all decimal
symbols, we need to use letters
to represent some digits in the
Hexadecimal system.

8. From hexadecimal to binary
As each hexadecimal number can be represented by four binary digits, then to
convert an hexadecimal number to binary we proceed as follows:
(7AF3)16 = ( ?)2
Starting from left to right each hexadecimal digit is replaced by its binary
representation:
7 = 0111 A = 1010 F = 1111 3 = 0011
0111 1010 1111 0011
Note: see the table in the previous slide.

9. From binary to hexadecimal
We need to convert the following binary number to hexadecimal:
(10111110111000)2 = ( ?)16
Starting from right to left we make groups of four bits. If the last group on
the right has less than four bits we add some padding zeros.
10111110111000
0010 1111 1011 1000
2FB8

10. From binary to hexadecimal
We need to convert the following binary number to hexadecimal:
(10111110111000)2 = ( ?)16
Starting from right to left we make groups of four bits. If the last group on
the right has less than four bits we add some padding zeros.
10111110111000
0010 1111 1011 1000
2FB8

11. Convert from decimal to binary: for example, (147)10 = ( ? )2
2 |147  1
2|73  1
2|36  0
2|18  0
2|9  1
2|4  0
2|2  0
2|1  1
0
Read
from
bottom
to
top
the number is: (10010011)2

12. Octal System  { 0, 1, 2, 3, 4, 5, 6, 7}
Decimal Binary Octal
0 000 0
1 001 1
2 010 2
3 011 3
4 100 4
5 101 5
6 110 6
7 111 7

13. Decimal Octal Binary hexadecimal
0 0 0000 0
1 1 0001 1
2 2 0010 2
3 3 0011 3
4 4 0100 4
5 5 0101 5
6 6 0110 6
7 7 0111 7
8 10 1000 8
9 11 1001 9
10 12 1010 A
11 13 1011 B
12 14 1100 C
13 15 1101 D
14 16 1110 E
15 17 1111 F

14. The End