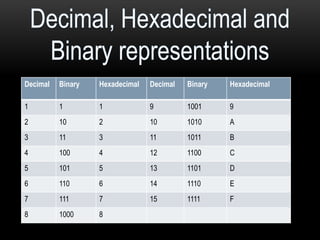
This document discusses different number systems including positional and non-positional, and how to convert between decimal, binary, octal, and hexadecimal numbers. It explains that positional systems use the digit's position and value to determine its overall value, and different bases determine the maximum single digit value. Conversion between number systems involves representing values in their respective bases then performing arithmetic operations.

2.  Non-Positional Number System
 Positional Number System

3.  Difficult to perform arithmetic operation.
 For example:- I, II, III, IV, V, VI, VII, VIII,
IX, X.

4.  The values of each digit is determined by:-
 -Digit itself
 -Position of the digit
 -Base of the number system

5.  The base is equal to 10.
 Uses 10 different symbols.

6.  The base is 2.
 Each position represents a power of the base 2.
 For example:- Conversion from 00111101 to decimal is-
 128 64 32 16 8 4 2 1
 0 0 1 1 1 1 0 1
=(0*128) + (0*64) + (1*32) + (1*16) + (1*8) + (1*4) + (0*2) + (1*1)
= 32 + 16 + 8 + 4 + 1
=(61)10

7.  The base is 8.
 Largest single digit is 7.

8.  The base is 16.
 Combination of 0-9 and A-F.

9. Decimal Binary Hexadecimal Decimal Binary Hexadecimal
1 1 1 9 1001 9
2 10 2 10 1010 A
3 11 3 11 1011 B
4 100 4 12 1100 C
5 101 5 13 1101 D
6 110 6 14 1110 E
7 111 7 15 1111 F
8 1000 8

16.  Convert each octal digit to 3-bit binary form.
 Combine all the 3 bits binary form.
 Divide the binary numbers into the 4-bit binary form.
 Convert these 4 bits blocks into their respective
hexadecimal symbols .

17. Example: Octal number is 2327
Octal Number 2 3 2 7
Binary Coded value 010 011 010 111
combining 3-bit blocks we have 010011010111
Dividing of binary numbers into 4-bit binary blocks and converting these
blocks into their respective symbols, we have 0100 1101 0111
4 D 7

18. Same procedure to convert
decimal number to binary, octal &
hexadecimal.
Same procedure to convert from
binary, octal & hexadecimal to
decimal numbers .