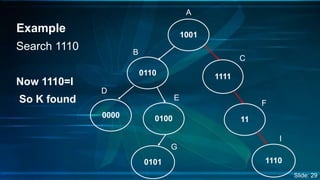
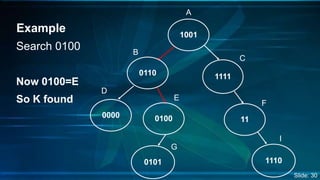
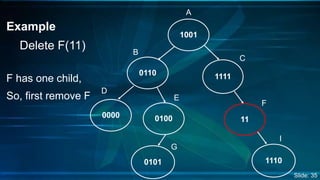
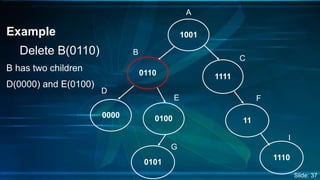
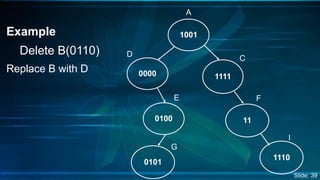
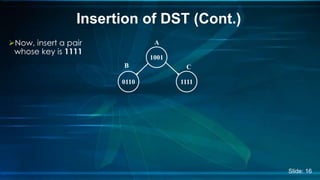
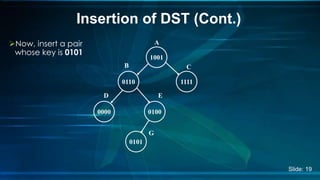
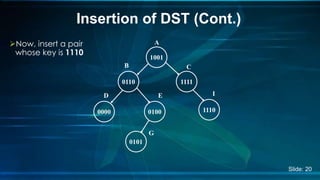
The document presents an overview of Digital Search Trees (DST), which are binary trees designed for efficient storage and retrieval of binary data based on bit representation. It discusses the structure, insertion, search, and deletion operations of DST, highlighting applications in IP routing (IPv4 and IPv6) and firewall systems. The document also addresses the benefits and drawbacks of DST compared to traditional binary search trees and AVL trees.

2. Presented By
Nayeem Hasan
ID: 2013-1-60-066
S.M.Sadman Sadid
ID: 2013-1-60-065
Tanzim Rizwan
ID: 2013-1-60-063
Department of Computer Science & Engineering
East West University
Slide: 1

3. OVERVIEW
Definition.
Structure.
Application.
Insertion.
Search.
Deletion.
Slide: 2

4. What is DST?
Definition
Digital search tree is one kind of binary tree which
contains only binary data.
If the bit of DST starts with 0 then it is in left subtree and if
the bit starts with 1 then it is in right subtree and this
process works recursively.
Slide: 3

5. Simple Structure(4 bits only)
****
0***
00**
001*
1***
10**
100*
11**
110*
Slide: 4

6. Digital Search Tree Example
A 00001
S 10011
E 00101
R 10010
C 00011
H 01000
A
S
R
E
C H
Slide: 5

7. Search Time Of DST
Searching is based on binary representation of data.
If the data are randomly distributed then the average
search time per operation in O(log N), where N is the
height of the tree.
However, Worst case is O(b), where b is the number
of bits in the search key.
Slide: 6

8. Application Of DST
IP routing.
IPv4 – 32 bit IP address.
IPv6 – 128 bit IP address.
Firewalls.
Slide: 7

9. What is IPv4 and IPv6?
IPv4 is the fourth generation of internet protocol version and the
most used version.
IPv4 uses 32 bit address which divided into four 8- bit parts and
which limits the address space to 4,294,967,296 (232 ) possible
unique address.
Slide: 8

10. IPv6 is the Internet's next-generation protocol and the current version of
internet protocol which replace the IPv4.
IPv6 uses 128- bit hexadecimal address which divides in 8 parts and each
part contains 16 bit binary number and which is designed to identification
and location system for computers on networks and routes traffic across the
Internet.
Slide: 9

11. What is firewall?
• A firewall is a network security system, either hardware or software based,
that controls incoming and outgoing network traffic based on a set of rules.
• Firewall is a software program or piece of hardware that helps screen out
hackers, viruses, and worms that try to reach your computer over the
Internet
Slide: 10

12. Insertion, search and deletion in DST are easier than
the Binary search tree and AVL tree.
This tree does not required additional information to
maintain the balance of the tree because the depth of
the tree is limited by the length of the key element.
DST requires less memory than Binary search tree and
AVL tree.
Benefit Of DST
Slide: 11

13. Drawbacks Of DST
Bitwise operations are not always easy.
Handling duplicates is problematic.
Similar problem with keys of different lengths.
Data is not sorted.
If a key is long search and comparisons are costly, this
can be problem
Slide: 12

14. Insertion of DST
 To insert an element in DST. There will be four(4) possible
cases.
 Tree Empty
 If found ‘0’, then go left
 If found ‘1’ then go right
 If found same key, then insert with prefix equal
Slide: 13

15. Insertion of DST (Cont.)
Start with an empty
digital search tree and
insert a pair whose key
is 1001
A
1001
Slide: 14

16. Insertion of DST (Cont.)
Start with an empty
digital search tree and
insert a pair whose key
is 1001
A
1001
Now, insert a pair
whose key is 0110
A
1001
B
0110
Slide: 15

17. Insertion of DST (Cont.)
Now, insert a pair
whose key is 1111
A
1001
B
0110
C
1111
Slide: 16

18. Insertion of DST (Cont.)
Now, insert a pair
whose key is 0000
A
1001
B
0110
C
1111
D
0000
Slide: 17

19. Insertion of DST (Cont.)
Now, insert a pair
whose key is 0100
A
1001
B
0110
C
1111
D E
0000 0100
Slide: 18

20. Insertion of DST (Cont.)
Now, insert a pair
whose key is 0101
A
1001
B
0110
C
1111
D E
0000 0100
0101
G
Slide: 19

21. Insertion of DST (Cont.)
Now, insert a pair
whose key is 1110
A
1001
B
0110
C
1111
D E
0000 0100
0101
G
I
1110
Slide: 20

22. Insertion of DST (Cont.)
Now, insert a pair
whose key is 11
A
1001
B
0110
C
1111
D E
0000 0100
0101
G
11
F
1110
I
Slide: 21

23. Insertion of DST (Cont.)
Now, insert a pair
whose key is 11
A
1001
B
0110
C
1111
D E
0000 0100
0101
G
11
F
I
1110
Slide: 22

24. Insertion Pseudo Code of DST
insert()
To insert an item, with a key, k, we begin a search from the root node to
locate the insertion position for the item.
 if t->root is null then
{
t->root = new node for the item with key k;
return null;
}
p = t->root;
i = max_b;
Slide: 23

25. loop
{
if p->key == k then a matching item has been found
return p->item;
i = i - 1; /*Traverse left or right branch, depending on the current bit.*/
let j be the value of the (i)th bit of k;
if p->a[j] is null then
{
p->a[j] = new node for the item with key k;
return null;
}
p = p->a[j];
}
Insertion Pseudo Code of DST
Slide: 24

26. Insertion Pseudo Code of DST
In the above pseudo-code, insertion fails if there is already an item with key
k in the tree, and a pointer to the matching item will be returned.
Otherwise, when insertion is successful, a null pointer is returned. When the
new node, x, is created, its fields are initialized as follows.
x->key = k;
x->item = item;
x->a[0] = x->a[1] = NULL;
Slide: 25

27. DST search for key K
Search
For each node T in the tree we have 4 possible results
T is empty
K matches T
Current bit of K is a 0 and go to left child
Current bit of K is a 1 and go to right child
Slide: 26

28. Example
Search 0001
NOT FOUND
A
1001
1111
11
0110
0000 0100
0101 1110
B
C
D
E
F
G
I
Slide: 27

29. Search 0000
Now 0000=D
So K found
1001
1111
11
0110
0000 0100
0101 1110
Example
A
B
C
D
E
F
G
I
Slide: 28

30. Search 1110
Now 1110=I
So K found
1001
1111
11
0110
0000 0100
0101 1110
Example
A
B
C
D
E
F
G
I
Slide: 29

31. Search 0100
Now 0100=E
So K found
1001
1111
11
0110
0000 0100
0101 1110
Example
A
B
C
D
E
F
G
I
Slide: 30

32. Struct node{
int key,info;
struct node *l,*r ;
}
static struct node *head,*z;
unsigned bits(unsigned x, int k, int j)
return (x>>k) & ~(~0<<j);
Int digital_search(int v)
{
struct node *x=head;
int b=maxb; // maxb is the number of bits in the key to be sorted
z->key=v;
while(v!=x->key)
x=(bits(v,b--,1) ? x->r : x->l;
return x->info;
}
C code of DST Search
Slide: 31

33. For each node T in the tree we have 3 possible cases.
 No child
 One child
 Two children
Delete
Slide: 32

34. Example
Delete G(0101)
A
1001
1111
11
0110
0000 0100
0101 1110
B
C
D
E
F
G
I
Slide: 33

35. Example
Delete G(0101)
G has no child,
So simply remove G
And replace
by a NIL pointer
A
1001
1111
11
0110
0000 0100
0101 1110
B
C
D
E
F
G
I
Slide: 34

36. Example
Delete F(11)
F has one child,
So, first remove F
A
1001
1111
11
0110
0000 0100
0101 1110
B
C
D
E
F
G
I
Slide: 35

37. Example
Delete F(11)
And link C with I
1001
0110 1111
0000 0100
0101
1110
A
B
C
D
E
G
I
Slide: 36

38. Example
Delete B(0110)
B has two children
D(0000) and E(0100)
1001
0110 1111
0000 0100
0101
11
A
B
C
D
E
G
F
I
1110
Slide: 37

39. Example
Delete B(0110)
Remove B and replace
with one of its child
1001
0110 1111
0000 0100
0101
11
A
B
C
D
E
G
F
I
1110
Slide: 38

40. Example
Delete B(0110)
Replace B with D
1001
0000 1111
0100
0101
11
A
C
D
E
G
F
I
1110
Slide: 39

41. 1001
1111
11
0000
0100
0101
1110
A
C
D
E
G F
I
Example
Delete B(0110)
OR
Replace B with E
Slide: 40

42. Delete Pseudo code of DST
1.Search key
2. if(key==Node)
free(Node);
if(Node->left==NULL && Node->right==NULL
Do Nothing;
else if(Node->left!=NULL)
Replace Node with next left Node
else if(Node->right!=NULL)
Replace Node with next right Node
else if(Node->right!=NULL && Node->left!=NULL )
Replace Node with next any Node
Slide: 41

43. Conclusion
The digital search trees can be recommended for use whenever
the keys stored are integers
Character strings of fixed width.
DSTs are also suitable in many cases when the keys are strings
of variable length.
Slide: 42

44. THANK YOU ALL !!!
Slide: 43