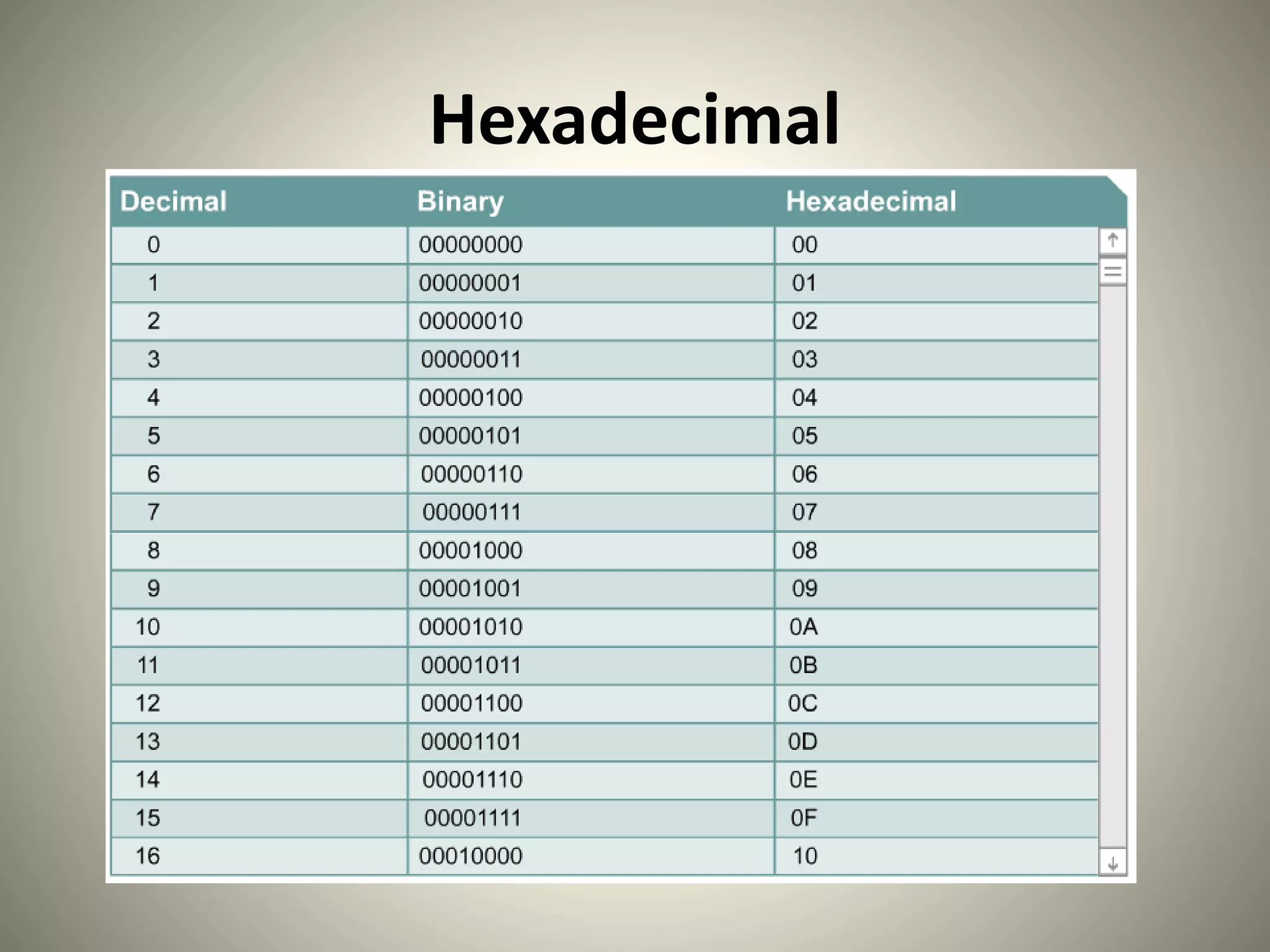
The document discusses different number systems used in computing such as binary, octal, decimal, and hexadecimal. It explains that computers use the binary system to represent information as either 1s or 0s. It then provides details on how to convert between the different number systems, including rules for place values and the meaning of each digit place. Converting between decimal, binary, octal, and hexadecimal is important for understanding computer networks and communications.

1. Number Systems
Imranul Hasan
Greenwich University, UK

2. Network Math
www.thinkgeek.com

3. Binary Mathematics
• It is very important to understand the concept
of Binary Mathematics as this is the language
which computers communicate in.
• Computers can only understand two states, on
which is represented by 1 and off which is
represented by 0 (Digital).
• But why do we need Digital???

4. Computers do Binary
1 0
• Bits have two values: OFF and ON
• The Binary number system (Base-2) can represent OFF
and ON very well since it has two values, 0 and 1
– 0 = OFF
– 1 = ON
• Understanding Binary to Decimal conversion is critical in
networking.

5. Number System Rules
• Some number systems are:
– Binary Number System – Base 2 (0, 1)
– Octal Number System – Base 8 (0, 1, 2, 3, 4, 5, 6, 7)
– Decimal Number System – Base 10 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
– Hexadecimal Number System – Base 16 (0, 1, 2, 3, 4, 5, 6, 7,
8, 9, A, B, C, D, E, F)

6. Number System Rules
• Each of the following columns is n times the previous column (n = Base-n)
– Base 2: 16 8 4 2 1
– Base 8: 4,096 512 64 8 1
– Base 10: 10,000 1,000 100 10 1
– Base 16: 65,536 4,096 256 16 1
N0N1N2N3 N-1 N-2
One’s
Tens
Hundreds
Thousands

7. Base 10 number system – The Math
The decimal number system: based on powers of 10.
23510 = (2x102) + (3x101) + (5x100)
100101102103 10-1 10-2
One’s
Tens
Hundreds
Thousands
532
5 one’s
3 tens
2 Hundreds

8. Base 2 (Binary) number system
• Converting Binary to Decimal:
101011= 1 x 25 + 0 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 1 x 20)
= 32 + 0 + 8 + 0 + 2 + 1
= 4310
= 1x8 + 1x4 + 0x2 + 1x1 = 8+4+0+1 = 1310
… Or … 1248
1 0 11
20212223
Binary PWC

9. Converting Decimal to Binary
Digits (2): 0, 1
Number of:
27 ___ ___ ___ 23 22 21
20
128’s 8’s 4’s 2’s
1’s
Dec.
2 1 0
10 1 0 1 0
17
70
130
255
•Another way is dividing decimal number by 2 and Multiplying by 2

10. Converting Decimal to Binary
Digits (2): 0, 1
Number of:
27 26 25 24 23 22 21
20
128’s 64’s 32’s 16’s 8’s 4’s 2’s
1’s
Dec.
2 1 0
10 1 0 1 0
17 1 0 0 0 1
70 1 0 0 0 1 1 0
130 1 0 0 0 0 0 1 0
255 1 1 1 1 1 1 1 1

11. Converting Decimal to Binary
Digits (2): 0, 1
Number of:
27 26 25 24 23 22 21
20
128’s 64’s 32’s 16’s 8’s 4’s 2’s
1’s
Dec.
1 0 0 0 1 1 0
1 0 1 0 0 0
0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0
172
192

12. Converting Decimal to Binary
Digits (2): 0, 1
Number of:
27 26 25 24 23 22 21
20
128’s 64’s 32’s 16’s 8’s 4’s 2’s
1’s
Dec.
70 1 0 0 0 1 1 0
40 1 0 1 0 0 0
0 0 0 0 0 0 0 0 0
128 1 0 0 0 0 0 0 0
172 1 0 1 0 1 1 0 0
192 1 1 0 0 0 0 0 0

13. Base 16 (Hexadecimal) Number
System
Digits (16):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E,
F
Decimal Hexadecimal Decimal
Hexadecimal
0 0 8 8
1 1 9 9
2 2 10 A
3 3 11 B
4 4 12 C
5 5 13 D
6 6 14 E
7 7 15 F

14. Base 16 (Hexadecimal) Number
System
Digits (16):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E,
F
Number of:
___ ___ 161 160
Dec. 16’s 1’s
8 ? ?
9
10
15
16
17

15. Base 16 (Hexadecimal) Number
System
Digits (16):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E,
F
Number of:
163 162 161 160
Dec. 4,096’s 256’s 16’s 1’s
8 8
9 9
10 A
15 F
16 1 0
17 1 1

16. Base 16 (Hexadecimal) Number
System
Digits (16):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E,
F
Number of:
163 162 161 160
Dec. 4,096’s 256’s 16’s 1’s
25
66
100
254
255

17. Base 16 (Hexadecimal) Number
System
Digits (16):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E,
F
Number of:
163 162 161 160
Dec. 4,096’s 256’s 16’s 1’s
25 1 9
66 4 2
100 6 4
254 F E
255 F F

18. Base 16 (Hexadecimal) Number
System
Digits (16):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B,
C, D, E, F
Number of:
163 162
161 160
Dec. 4,096’s 256’s 16’s
1’s
? 1 A
C
? 2 0 3

19. Base 16 (Hexadecimal) Number
System
Digits (16):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B,
C, D, E, F
Number of:
163 162
161 160
Dec. 4,096’s 256’s 16’s
1’s
428 1 A C
515 2 0 3

20. Hexadecimal

21. Why Hexadecimal?
• Hexadecimal is perfect for matching 4 bits.
• 16 Hex values which means 16 4 bit possibilities.
• 4 bits can be represented by 1 Hex value
• 8 bits (1 byte or octet) can be represented by 2 Hex
values
Dec. Hex. Binary Dec. Hex. Binary
8421 8421
0 0 0000 8 ? ?
1 ? ? 9
2 10
3 11
4 12
5 13
6 14
7 15

22. Decimal - Hexadecimal - Binary
Dec. Hex. Binary Dec. Hex. Binary
8421 8421
0 0 0000 8 8 1000
1 1 0001 9 9 1001
2 2 0010 10 A 1010
3 3 0011 11 B 1011
4 4 0100 12 C 1100
5 5 0101 13 D 1101
6 6 0110 14 E 1110
7 7 0111 15 F 1111

23. Why Hex?
Hexadecimal is an easy way to represent a string of bits.
Here are 48 bits being transmitted:
000000000010000011100000011010110001011101100010
Break them up into 4 bit chunks:
0000 0000 0010 0000 1110 0000 0110 1011 0001 0111 0110 0010
Convert each 4 bits to Hexadecimal:
0 0 2 0 E 0 6 B 1 7 6 2

24. Base-n to Decimal Conversion
(1101.101)2 = 123 + 122 + 120 + 12-1 + 12-3
= 8 + 4 + 1 + 0.5 + 0.125 = (13.625)10
(572.6)8 = 582 + 781 + 280 + 68-1
= 320 + 56 + 2 + 0.75 = (378.75)10
(2A.8)16 = 2161 + 10160 + 816-1
= 32 + 10 + 0.5 = (42.5)10
(341.24)5 = 352 + 451 + 150 + 25-1 + 45-2
= 75 + 20 + 1 + 0.4 + 0.16 = (96.56)10
N0N1N2N3 N-1 N-2
One’s
Tens
Hundreds
Thousands

25. Binary to Octal/Hexadecimal
Conversion
Binary  Octal: Partition in groups of 3
(10 111 011 001 . 101 110)2 = (2731.56)8
Octal  Binary: reverse
(2731.56)8 = (10 111 011 001 . 101 110)2
Binary  Hexadecimal: Partition in groups of 4
(101 1101 1001 . 1011 1000)2 = (5D9.B8)16
Hexadecimal  Binary: reverse
(5D9.B8)16 = (101 1101 1001 . 1011 1000)2

26. Any Questions?
Mail Me @ : suvrolinss@gmail.com