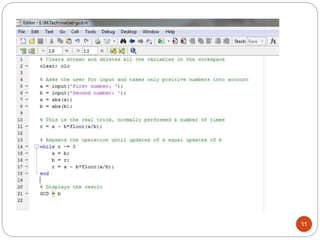
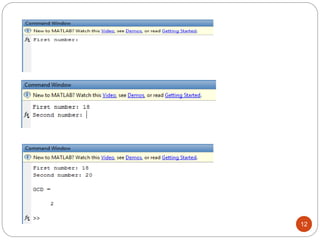
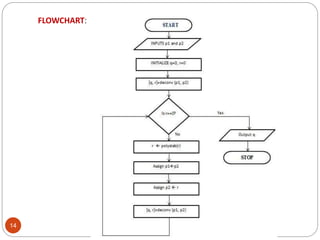
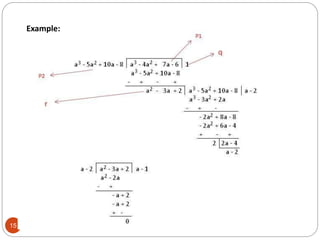
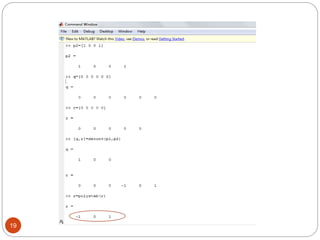
This document discusses the Euclidean algorithm for finding the greatest common divisor (GCD) of integers and polynomials. It begins with an introduction and definitions of GCD and the Euclidean algorithm. It then provides the steps of the Euclidean algorithm, applications, and MATLAB code examples to calculate the GCD of integers and polynomials. The document concludes with future work plans to improve the polynomial GCD MATLAB code and implement GCD algorithms in Verilog code targeting FPGAs.

1. Project Associates:
ABHISHEK - 1PI14LVS01
APARNA BHAT - 1PI14LVS02
ASHWINI SHENOY - 1PI14LVS03
CHAITRA ALASE G -
1PI14LVS04
SWAMY J S - 1PI14LVS17
EUCLIDEAN ALGORITHM FOR
GCD OF
INTEGERS AND POLYNOMIALS

2. CONTENTS
2
 Introduction
 GCD
 Euclidean GCD
 Applications of Euclidean Algorithm
 Flowchart
 MATlab code for integers
 GCD for Polynomials.
 MATlab Functions
 Future work

3. GCD
3
 In mathematics, the greatest common divisor (gcd) of two
or more integers, when at least one of them is not zero, is
the largest positive integer that divides the numbers
without a remainder.
 The GCD is also known as the greatest common
factor (gcf), highest common factor (hcf), greatest
common measure (gcm), or highest common divisor.

4. Euclidean GCD
4
 It is named after the ancient Greek mathematician Euclid,
who first described it in Euclid’s Elements (c. 300 BC)
 Efficient algorithm to calculate GCD is Euclidean GCD.
 Uses a division Algorithm.
 The Euclidean algorithm is based on the principle that the
greatest common divisor of two numbers does not change
if the larger number is replaced by its difference with the
smaller number.

5. CONTD…
5
 The original algorithm was described only for natural
numbers and geometric lengths (real numbers), but
the algorithm was generalized in the 19th century to
other types of numbers, such as Gaussian
integers and polynomials of one variable. This led to
modern abstract algebraic notions such as Euclidean
domains.

6. Applications of Euclidean Algorithm
6
 The Euclidean algorithm has many theoretical and practical
applications.
 It is used for reducing fractions to their simplest form and
for performing division in modular arithmetic.
 cryptographic protocols that are used to
secure internet communications.
 The Euclidean algorithm may be used to solve Diophantine
equations.
 It is a basic tool for proving theorems in number
theory such as Lagrange’s four-square theorem and
the uniqueness of prime factorizations.

7. Euclidean Algorithm:
7
 GCD(a,b) where a and b are integers.
 For all a , b with a > b there is a q (quotient) and
r (remainder) such that
a = qb + r
with r < b or r = 0
 This is calculated repeatedly by making a=b and
b=r until r=0.
 Finally, GCD=b.

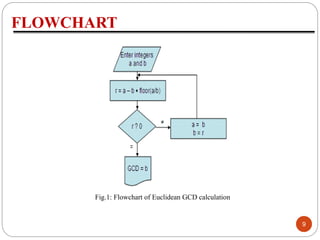
8. Properties of GCD:
8
 Gcd(a,0)=a
 Gcd(a,a)=a
 Gcd(a,b)=gcd(b,a mod b)
 a mod b=a-b [floor(a/b)]

9. FLOWCHART
9
Fig.1: Flowchart of Euclidean GCD calculation

10. MATLAB CODE
10
clear; clc
a = input('First number: ');
b = input('Second number: ');
a = abs(a);
b = abs(b);
r = a - b*floor(a/b);
while r ~= 0
a = b;
b = r;
r = a - b*floor(a/b);
end
GCD = b

11. 11

12. 12

13. 13
GCD OF POLYNOMIALS
Definition: The greatest common divisor of two polynomials is a
polynomial, of the highest possible degree, that is a factor of both
the original polynomials.
• In of univariate polynomials , the polynomial GCD can be
computed, like that for the integer GCD, by Euclid's algorithm
using long division.
• The similarity between the integer GCD and the polynomial GCD
allows us to extend some properties of integer GCD to
polynomial GCD.
Property: The roots of the GCD of two polynomials are the common
roots of the two polynomials.
This allows to get information on the roots without computing
them.

14. 14
FLOWCHART:

15. 15
Example:

16. 1) De-convolution(p1,p2)=polynomial division(p1/p2)
16 Polynomial Division:
Q
P2
P1
R

17. 17
MATLAB deconv command execution:

18. 18
function b = polystab(a)
r = roots(a);
v = find(abs(r)>1); //finds indices of the vector “r” whose absolute value is
greater than 1
r(v) = 1./conj(r(v));
b = a(1) * poly ( r );
if isreal(a), b = real(b); endif
endfunction
2) Polystab(p1): Stabilizing the polynomial transfer
function

19. 19

20. 20

21. 21
FUTURE WORK:
• Rectify errors in MATLAB code for GCD of polynomials.
• Write Verilog code for GCD of two integers and dump the same into FPGA.
• Write Verilog code for GCD of two Polynomials.

22. 22
Thank you!!