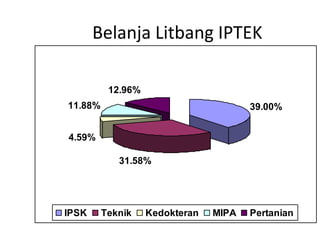
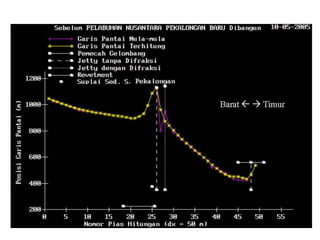
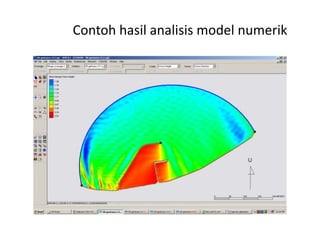
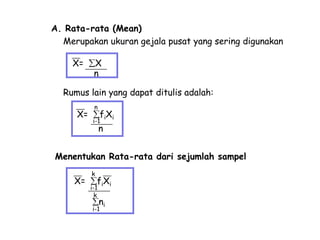
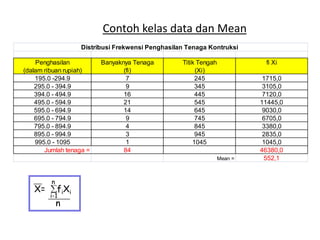
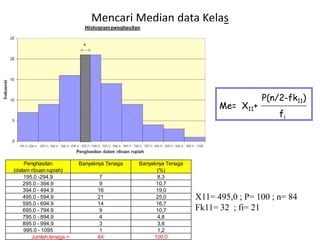
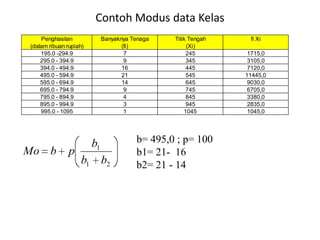
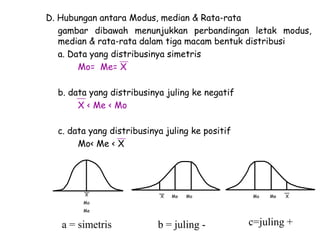
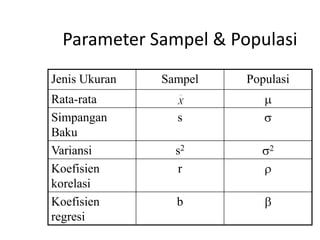
Dokumen ini membahas tentang statistika, termasuk pengertian, jenis, dan peranannya dalam kehidupan sehari-hari serta penelitian. Selain itu, dijelaskan juga mengenai pengukuran, data statistik, serta analisis dengan metode deskriptif dan inferensial. Pengukuran validity, penggolongan penelitian, dan ukuran gejala pusat, termasuk mean, median, dan modus, juga diuraikan secara rinci.

2. SISTEMATIKA MATERI
1.
2.
3.
4.
5.
6.
7.
PENDAHULUAN
TABEL & GRAFIK
UKURAN GEJALA PUSAT
UKURAN DISPERSI & VARIASI
REGRESI LINEAR SEDERHANA
POPULASI DAN SAMPLING
DISTRIBUSI NORMAL

3. A. Statistika dalam Kehidupan Sehari-hari
Kemajuan ilmu pengetahuan dan teknologi
tidak dapat dipisahkan dari statistika
Jaeger (1990) menyimpulkan bahwa statistika
tidak dapat dipisahkan dari kehidupan para
peneliti, pendidik, manajer, analis olahraga,
analis politik, pengusaha & hampir semua
orang yang terdidik.
Keperluan akan statistika berbeda-beda, baik
tingkat kedalamannya maupun jenis tekniknya

4. B. Pengertian dan Jenis Statistika
Statistika adalah bagian dari matematika yang secara
khusus membicarakan cara-cara pengumpulan, analisis dan
penafsiran data.
 Jenis Statistika berdasarkan pembahasannya:
- Matematika /statistika teoritis yang lebih berorientasi
pada pemahaman model & teknik-teknik statistika secara
matematis.
- Statistika Terapan: Bagian matematika yg secara khusus
membicarakan cara2 analisis dan panafsiran data
(interpretasi). Yang lebih berorientasi pada pemahaman
intuitif atas konsep & teknik-teknik statistika serta
penggunaannya di berbagai bidang.

5.  Jenis Statistika berdasarkan Tahapan Tujuan Analisisnya:
- Statistika Deskriptif
untuk memperoleh gambaran/ ukuran-ukuran tentang data
yang ada di tangan (ukuran sampel, ukuran populasi)
- Statistika Inferensial (to infer = menyimpulkan)
Kita dapat menggunakan data & ukuran sampel untuk
melakukan inferensi tentang populasi (statistika inilah yang
disebut statistika inferensial):
- Menaksir ukuran
- Menguji hipotesis

6.  Berdasarkan asumsi mengenai distribusi populasi data yang
dianalisis, statistika Inferensial dibedakan menjadi:
1. Statistika Parametrik
Jenis ini didasarkan pada model distribusi normal
2. Statistika Nonparametrik
Statistik ini tidak didasarkan pada suatu model distribusi
tertentu
 Statistika juga dibedakan berdasarkan jumlah peubah
(variabel) terikat (dependent variabel) yang dianalisis:
 statistika unvariat : 1 variabel terikat
 statistika multivariat : 2 atau lebih variabel terikat

7. C. Pengukuran & Data Statistik
1.
Pentingnya pengukuran dalam penelitian
Teknik statistik bukanlah prosedur yang dapat mengubah sampah
menjadi kertas atau pupuk yang berharga.
Pengukuran merupakan kegiatan untuk menyediakan data yang
akan dijadikan masukan dalam analisis statistika.
Validitas penelitian antara lain amat bergantung pada validitas
data yang diperoleh.
Jika data yang diperoleh tidak valid maka kegiatan analisis &
penafsiran data yang mengikutinya tidak valid.

8. 2.
Jenis data & skala pengukuran Kuantitatif
Data dapat digolongkan menjadi data diskrit & data
kontinu.
Data diskrit: Banyaknya anak di suatu keluarga, jumlah
rumah di suatu desa, banyaknya penduduk disuatu daerah,
dan jumlah mobil di kantor tertentu (merupakan bilangan
bulat)
Data kontinu: tingkat kecerdasan, prestasi belajar, berat
badan, dan daya tahan mobil merupakan contoh data
kontinu (termasuk bilangan desimal)

9. Dilihat dari skala pengukuran yang digunakan, data dibagi menjadi menjadi
4 jenis yang bersifat hirarkis, yaitu:
1. Data Nominal
Data ini memiliki skala yang bersifat kategorikal /
pengelompokan (jenis kelamin, warna kulit, agama), digunakan untuk
mengenali identitas subyek.
2. Data Ordinal
Data ini memiliki skala yang menunjukkan perbedaan
tingkatan subjek secara kuantitatif (data yang dinyatakan
dalam bentuk peringkat atau rangking)
Data ini selain memiliki sifat yang dimiliki data nominal juga
menunjukan kedudukan subjek dalam suatu kelompok pada
suatu variabel. Termasuk aplikasi skala likert
3. Data Interval
Selain memiliki kedua ciri diatas, data ini juga memiliki sifat kesamaan
jarak (equality of interval) antara nilai yang satu dengan nilai yang lain
4. Data Rasio
Hasil pengukuran merupakan contoh data rasio panjang (M), berat (kg).
Data rasio dapat disusus dalam data interval dan ordinal.

10. D. Penelitian Kuantitatif
Menurut Sukaji, 1992: kemajuan pesat negara2 industri maju
dan negara2 industri baru ternyata lebih tergantung pada mutu
SDM, kegiatan penelitian serta inovasi teknologi daripada
Sumberdaya alam.
1.
Memahami makna penelitian
Gay (1982), merumuskan penelitian sebagai suatu proses
sistematis untuk menjawab suatu pertanyaan.
Nasution (1992), menggambarkan sifat-sifat penelitian, yaitu
penelitian adalah suatu upaya pengkajian yang cermat, teratur &
tekun mengenai suatu masalah.
2.
Penggolongan penelitian
- Penelitian eksperimental: termasuk eksperimen semu
yang tidak melakukan random assigment. Penelitian
eksperimental dari penelitian lainnya adalah
adanya manipulasi peubah bebas.
- Penelitian Korelasional
Penelitian korelasional sendiri merupakan Penelitian yang
peubah bebasnya tidak dimanipulasi

11. 3. Penggolongan peubah penelitian
Beberapa jenis peubah yang sangat penting dipahami antara
lain (4):
a. Peubah bebas, yaitu peubah yang mempengaruhi peubah
lain
b. Peubah terikat, yaitu peubah yang dipengaruhi oleh
peubah lain
c. Peubah Moderator, yaitu peubah yang mempengaruhi
secara jelas (terukur) hubungan antara peubah bebas dengan
peubah terikat (memperkuat / memperlemah hubungan),
misal kehadiran anak dalam hub keluarga
d. Peubah Intervening, yaitu mempengaruhi variabel bebas &
terikat tetapi tidak terukur, antara IQ dan nilai ujian tetapi
ada intervening kondisi anak
e. Peubah Kontrol, yaitu peubah yang pengaruhnya kepada
peubah terikat dikendalikan. Misal mempertahankan
temperatur dalam eksperimental.

12. 4. Hubungan Antara Peubah Penelitian
1. Hubungan Kausal (pengaruh)
2. Hubungan Korelasional
3. Hubungan Perbandingan
5. Validitas Penelitian
Validitas penelitian diklasifikasikan menjadi:
1. Validitas Internal, berkaitan dengan keyakinan peneliti
tentang kesahihan hasil penelitian
2. Validitas Eksternal, berkaitan dengan tingkat generalisasi
penelitian yang diperoleh
 Validitas Internal dapat ditingkatkan dengan cara kumulatif
a. Melakukan pengukuran yang valid & reliabel atas seluruh
peubah yang dikaji
b. Mengontrol peubah yang diduga mempengaruhi peubah
terikat

13.  Penelitian eksperimen di laboratorium biasanya memiliki
validitas yang lebih tinggi dibandingkan dengan penelitian
lapangan
 Salah satu yang mendukung validitas eksternal suatu
penelitian adalah pemilihan subjek secara acak, sehingga
sampel yang diteliti dapat mewakili populasi yang diharapkan.
 Perbedaan validitas internal & validitas eksternal biasanya
lebihmudah dikendalikan pada penelitian lapangan daripada
penelitian laboratoris

14. Paradigma Penelitian
(pola pikir yang menunjukkan hubungan antara variabel penelitian)
1.
2.
3.
4.
5.
6.
7.
Paradigma sederhana
Paradigma sederhana berurutan
Paradigma ganda dengan 2 variabel independen
Paradigma ganda deang 3 variabel independen
Paradigma ganda dengan 2 variabel dependen
Paradigma Jalur sederhana
Paradigma jalur ganda

15.  Data statistik dan hasil penelitian sering disajikan dalam
bentuk tabel & grafik. Sebuah grafik atau tabel dapat
mewakili ratusan atau ribuan kata dalam suatu bentuk yang
kompak dan menarik.
A. Daftar Distribusi Frekuensi
Langkah-langkah adalah:
1. Menentukan rentang
2. Menentukan panjang kelas
3. Menentukan banyak kelas
4. Menyusun interval kelas
5. Menghitung frekuensi untuk setiap kelas

16. 1. Rentang:
Suatu perangkat data yang biasanya dilambangkan dengan
huruf R adalah skor terbesar dikurangi skor terkecil.
R= Nilai terbesar – Nilai terkecil
2. Banyak Kelas:
Banyak kelas menunjukkan jumlah interval kelas yang
diperlukan untuk mengelompokan suatu perangkat data
(Rumus Sturges).
bk=1+3,3 log n
3. Panjang Kelas:
Panjang kelas (p) atau interval (I) menunjukkan banyaknya
angka (nilai) yang tercakup oleh suatu interval kelas
P
R
bk

17. 4. Interval Kelas:
Untuk menyusun interval kelas, perlu ditentukan dahulu
bilangan awal untuk interval kelas pertama (paling bawah)
- merupakan kelipatan dari P
- < skor terkecil
5. Frekuensi:
Frekuensi setiap kelas dapat diperoleh dengan cara mentally
(turus) setiap nilai yang ada pada interval kelas masingmasing dan kemudian menjumlahkan banyaknya tally (turus)
yang didapat

18. Contoh
• Berdasar pengumpulan data didapat:
– Jumlah data sebanyak 100
– Range data antara minimal 1 dan maksimal 80
• Tentukan:
– Banyak nya kelas
– Panjang kelas
– Bentuk tabelnya

20. B. Grafik
Perangkat data statistik dapat ditampilkan secara visual
dalam bentuk grafik
1. Histogram
Merupakan suatu grafik yang menggambarkan sebaran
frekuensi suatu perangkat data dalam bentuk batang
2. Frekuensi Poligon
pada Histogram diasumsikan bahwa skor-skor pada interval
kelas meyebar secara merata.
Contoh dalam Excel 

21. Analisis Data Secara Grafik
• Secara umum, bidang studi statistik deskriptif adalah menyajikan data dalam
bentuk tabel dan grafik. Bentuk grafik yang sering dipakai dalam analisis adalah
grafik batang, pie, dan histogram.
• Histogram adalah diagram yg paling penting digunakan utk menyajikan data dari
suatu tabel frekuensi, dimana masing-masing frekuensi diwakili oleh suatu blok.
Setiap blok dlm histogram menunjukkan suatu frekuensi utk suatu interval kelas.
Sumbu horizontal menunjukkan pembagian kelas, sedangkan sumbu vertikal
menunjukkan frekuensinya.
100
%
90
frekuensi kurang dari
80
70
60
50
40
30
20
10
0
195.0
294.9
394.9
494.9
594.9
694.9
Penghasilan dalam ribuan rupiah
794.9
894.9
994.9

22. Belanja Litbang IPTEK
12.96%
11.88%
39.00%
4.59%
31.58%
IPSK
Teknik
Kedokteran
MIPA
Pertanian

24. Contoh hasil analisis model numerik

25. Analisis yang menyajikan deskripsi data
yang ada terpusat dimana?
• Mean (Rata-rata)
• Median (Nilai Tengah)
• Modus (Nilai paling sering muncul)
• Hubungan Mean, Median dan Modus
• Kuartil, desil & Persentil

26. A. Rata-rata (Mean)
Merupakan ukuran gejala pusat yang sering digunakan
X=
X
n
Rumus lain yang dapat ditulis adalah:
X=
n
fiXi
i-1
n
Menentukan Rata-rata dari sejumlah sampel
X=
k
fiXi
i-1
k
ni
i-1

27. Contoh kelas data dan Mean
Distribusi Frekwensi Penghasilan Tenaga Kontruksi
Penghasilan
(dalam ribuan rupiah)
195.0 -294.9
295.0 - 394.9
394.0 - 494.9
495.0 - 594.9
595.0 - 694.9
695.0 - 794.9
795.0 - 894.9
895.0 - 994.9
995.0 - 1095
Jumlah tenaga =
Banyaknya Tenaga
(fi)
7
9
16
21
14
9
4
3
1
84
Titik Tengah
(Xi)
245
345
445
545
645
745
845
945
1045
fi Xi
Mean =
X=
n
fiXi
i-1
n
1715,0
3105,0
7120,0
11445,0
9030,0
6705,0
3380,0
2835,0
1045,0
46380,0
552,1

28. B. Median
merupakan titik/ nilai yang membagi seperangkat data
menjadi dua bagian sama banyak
Me= X11+
P(n/2-fk11)
fi
dimana:
Me : Median
X11 : batas nyata bawah kelas median
p : panjang kelas
n : banyak data
fk11: frekuensi kumulatif interval kelas di bawah kelas median
fi : frekuensi kelas median

29. Mencari Median data Kelas
Me= X11+
Penghasilan
(dalam ribuan rupiah)
195.0 -294.9
295.0 - 394.9
394.0 - 494.9
495.0 - 594.9
595.0 - 694.9
695.0 - 794.9
795.0 - 894.9
895.0 - 994.9
995.0 - 1095
Jumlah tenaga =
Banyaknya Tenaga
7
9
16
21
14
9
4
3
1
84
Banyaknya Tenaga
(%)
8,3
10,7
19,0
25,0
16,7
10,7
4,8
3,6
1,2
100,0
P(n/2-fk11)
fi
X11= 495,0 ; P= 100 ; n= 84
Fk11= 32 ; fi= 21

30. C. Modus
Merupakan nilai yang paling sering muncul dalam suatu pengukuran
- kasus sederhana
- kasus interval klas
Mo b
p
b1
b1
b2
dimana:
b : batas bawah interval kelas dengan frekuensi terbanyak
p : panjang kelas
b1 : frekuensi terbanyak - frekuensi kelas sebelumnya
b2: frekuensi terbanyak - frekuensi kelas sesudahnya

31. Contoh Modus data Kelas
Penghasilan
(dalam ribuan rupiah)
195.0 -294.9
295.0 - 394.9
394.0 - 494.9
495.0 - 594.9
595.0 - 694.9
695.0 - 794.9
795.0 - 894.9
895.0 - 994.9
995.0 - 1095
Mo b
p
Banyaknya Tenaga
(fi)
7
9
16
21
14
9
4
3
1
b1
b1
b2
Titik Tengah
(Xi)
245
345
445
545
645
745
845
945
1045
b= 495,0 ; p= 100
b1= 21- 16
b2= 21 - 14
fi Xi
1715,0
3105,0
7120,0
11445,0
9030,0
6705,0
3380,0
2835,0
1045,0

32. D. Hubungan antara Modus, median & Rata-rata
gambar dibawah menunjukkan perbandingan letak modus,
median & rata-rata dalam tiga macam bentuk distribusi
a. Data yang distribusinya simetris
Mo= Me= X
b. data yang distribusinya juling ke negatif
X < Me < Mo
c. data yang distribusinya juling ke positif
Mo< Me < X
X
X
Me
Mo
Mo
Me
X
Mo
Me
a = simetris
b = juling -
c=juling +

33.  Dalam kegiatan penelitian, rata-rata lebih sering digunakan
kepada ukuran lainnya karena peneliti tidak hanya hendak
menggambarkn keaadaan sampel, tapi juga ingin melakukan
referensi tentang keadaan populasinya
F. Kuartil, desil & Persentil
sejalan dengan konsep median kita juga memiliki ukuran
statistik yang dikenal dengan sebutan kuartil, desil &
persentil
Tiga nilai kuartil (K1, K2 dan K3), sembilan nilai desil (D1-D9)
dan 99 nilai persentil (Pi-P99)
K2 = D5 = P50 = Median, K1 = P25 dan D6 = P60

34. Parameter Sampel & Populasi
Jenis Ukuran
Rata-rata
Simpangan
Baku
Variansi
Koefisien
korelasi
Koefisien
regresi
Sampel
X
s
s2
r
b
Populasi

35.  Statistika sering disebut studi tentang variasi karena
membahas dan menyediakan cara-cara untuk menyelidiki
variasi gejala alam sosial serta membuat kesimpulan tentang
hal-hal yang melatar belakangi terjadinya variasi (Ferguson &
Takane, 1989)
 Para ahli statistika telah mengusulkan sejumlah ukuran yang
dapat membantu memahami variasi suatu perangkat data.
Rentang dapat diartikan sebagai selisih antara skor terbesar
dan skor terkecil pada suatu perangkat data
A. Rentang (R)
Merupakan ukuran yang paling sederhana dan kasar tentang
variasi suatu perangkat data. Rentang dapat diartikan juga
sebagai selisih antara skor terbesar dan skor terkecil pada
suatu perangkat data

36.  Rentang jarang digunakan utuk menggambarkan variasi
perangkat data, karena beberapa alasan berikut yang saling
berkaitan (Shavelson, 1988: Ferguson & Takane, 1989):
1. Rentang merupakan ukuran yang tidak stabil
2. Rentang tidak mencerminkan pola variasi suatu distribusi
data
3. Rentang bergantung pada besarnya sampel (n)
B. Rentang Antar Kuartil
RAK = K3-K1
= P75-P25
dimana:
RAK: Rentang Antar Kuartil
K1 : Nilai kuartil ke-1
K2 : Nilai kuartil ke-2
P75 : Nilai persentil ke-75
P25 : Nilai persentil ke-25

37. C. Rata-rata Simpangan
merupakan jumlah harga mutlak skor simpangan dibagi
dengan banyaknya data (n)
x=
n
[Xi-X]
n=1
n
D. Variasi (s2) dan Simpangan Buku (s)
Merupakan dua buah ukuran yang paling sering digunakan
tentang variasi suatu perangkat data
Variasi adalah kuadrat dari simpangan baku, & sebaliknya,
simpangan baku adalah akar.

38.  Contoh, mengambil sampel yang terdiri dari 40 subjek dari
suatu populasi. Secara teoritis, populasi itu terdiri dari N
subjek (N= jumlah anggota populasi) yang memiliki
parameter tertentu. Seperti rata-rata ( ) dan variasi ( 2).
Sampel dilambangkan dengan huruf n (disini n= 40). Secara
teknis, variasi sampel tersebut kemudian dapat ditentukan
dengan rumus:
S2
=
n
i=1
(Xi - )2
n
dimana:
S2 : variasi sampel
Xi : skor (nilai) ke-I pada suatu perangkat data
: rata-rata populasi
n : jumlah populasi (banyaknya data)
Merupakan cara menentukan sampel yang tidak bias
terhadap variasi populasinya.

39.  Cara menentukan sampel yang tidak bias terhadap variasi
populasinya.
Variasi sampel dapat ditulis kembali menjadi rumus:
S2
=
n
i-1
(Xi -X)2
n-1
Untuk jumlah data populasi dibagi n
Untuk jumlah data sampel dibagi n-1
 Simpangan baku adalah akar dua dari variasi seperti
terlihat pada rumus diatas. Simpangan baku yang sering
dilambangkan dengan huruf s untuk simpangan baku sampel
dan untuk simpangan baku populasi
makin bervariasi suatu perangkat data makin besarlah
simpangan bakunya, dan sebaliknya
S
S
2

40.  Besaran variasi dan simpangan baku sangat bergantung pada
skala data. Data yang dicatat dalam skala satuan cenderung
memiliki simpangan baku yang lebih kecil daripada data yang
dicatat dalam skala puluhan
 Perlu dicari suatu ukuran variasi yang tidak terlalu
tergantung kepada skala data. Masalah ini memunculkan
pemikiran untuk menggunakan rasio simpangan baku
terhadap rata-ratanya yang kemudian dikenal istilah
koefisien variasi (KV) yang dapat diperoleh dengan
menggunakan rumus
KV= s
X
 Variasi antara suatu perangkat data dapat dibandingkan
dengan variasi perangkat data lain dengan cara
membandingkan kaefisien variasinya tanpa harus khawatir
terhadap skala datanya karena koefesien variasi telah
memperhitungkan perbedaan skala data.

41. Contoh Sederhana
• Data: 2, 2, 3, 3, 4, 4, 5, 5, 6, 6
• Tentukan:
– Rata2 (mean)
2
– Variasi (s )
– Simpangan Baku (s)
– Koefisien variasi (KV)

42. E. Skor Baku (z)
merupakan skor mentah dikurangi rata-ratanya
skor baku (yang dikembangkan dengan z dan
dikenal dengan sebutan z-score) dapat diperoleh
dengan rumus
_
z
xi
x
S
Statistika inferensial banyak menggunakan
distribusi normal baku (standart normal
distribution) sebagai model distribusi data yang
hendak dianalisis. Distribusi normal baku itu
tidak lain adalah distribusi seperangkat skor
baku (z) sehingga dikenal dengan istilah
distribusi z (z-distribution)

43. Tugas 1
• Buat/ Kumpulkan kira-kira 40 data sesuai
bidang tugas.
• Tentukan Rentang data, Jumlah Kelas dan
Panjang kelas
• Tentukan jumlah masing-masing kelas
• Tentukan ukuran tendensi sentral:
– Mean, Median dan Modus
• Tentukan jenis distribusi datanya

44. Tugas 2
Dari data tugas 1, tentukan:
a. Variansi (s2)
b. Simpangan baku (s)
c. Koefisien Variasi (KV)

45. 
Istilah ini digunakan untuk analisis regresi yang melibatkan sebuah
peubah bebas (X) dan sebuah peubah terikat (Y) . Pemahaman atas
regresi linier sederhana ini merupakan dasar untuk memahami
regresi linier jamak (multiple linier regretion) dan model regresi
lainnya.

Model Regresi sederhana mengatakan pada kita bahwa setiap nilai
pada peubah Y merupakan jumlah dari tiga komponen, yaitu
Intercept, koefesien regresi kali nilai pada peubah X, dan galat
prediksi ( R )
ˆ
y
1
Intercept
koefisien regresi
X1

46. Menemukan Harga
0
ˆ
1
Y
n
n
1
dan
1
X
xy
x2
0
x
y
x) 2
(
Kolom tabel yang diperlukan untuk menemukan koefesien
dengan menggunakan rumus
No
X
Y
X2
XY
1
2
3
4
5
6
7
8
7
7
5
4
3
2
10
8
9
6
5
2
2
64
49
49
25
16
9
4
80
56
63
30
20
6
4
1

47. No
x
y
x2
xy
y2
1
10
64
80
100
2
7
8
49
56
64
3
7
9
49
63
81
4
5
6
25
30
36
5
4
5
16
20
25
6
3
2
9
6
4
7
2
2
4
4
4
36
rata2
8
42
216
259
314
5.142857
6
11
10
9
8
7
6
5
4
3
2
1
0
y = 1.393x - 1.166
R² = 0.966
Series1
Linear (Series1)
Linear (Series1)
0
1
2
3
4
5
6
7
8
9

48. •
Koefisien Korelasi ( r )
1,00 r
1,00
xy
n 1
r
x2
n 1
Interval (r)
y2
n 1
Tingkat hubungan
0,00 – 0,199
Sangat rendah
0,20 – 0,399
Rendah
0,40 – 0,599
Sedang
0,60 – 0,799
Kuat
0,80 – 1,00
Sangat kuat

49. 6. Populasi dan Sampling
Populasi adalah obyek/subyek yang mempunyai
kuantitas dan karakteristik tertentu yang ditetapkan
oleh peneliti untuk dipelajari, dan kemudian ditarik
kesimpulannya.
Sampel adalah sebagian dari jumlah dan karakteristik
yang dimiliki oleh populasi tersebut.
Apabila populasi besar, dan peneliti tidak mungkin
mempelajari semua yang ada pada populasi
(misalnya karena keterbatasan dana, tenaga dan
waktu), maka peneliti dapat menggunakan sampel
yang diambil dari populasi itu. Hal demikian biasa
disebut dengan metode sampling.

50. Kriteria sampel yang representatif tergantung pada dua
aspek yang saling berkaitan, yaitu:
a) Akurasi sampel
Sampel yang akurat adalah sejauh mana statistik sampel
dapat mengestimasi
parameter populasi dengan tepat.
Akurasi berkaitan dengan tingkat keyakinan (confidence
level). Semakin akurat suatu sampel, akan semakin tinggi
tingkat keyakinan bahwa statistik sampel mengestimasi
parameter dengan tepat.
b) Presisi sampel
Sampel yang presisi adalah sejauh mana penelitian
berdasarkan sampel dapat merefleksikan realitas populasinya
dengan teliti. Presisi menunjukkan tingkat ketepatan
hasil
penelitian berdasarkan sampel yang menggambarkan
karakteristik populasinya.

51. Skema dan Teknik
Sampling
Probability sampling
1. Simple random sampling
2. Proportionate stratified
random sampling
3. Disproportionate stratified
random sampling
4. Area (cluster) sampling
Teknik Sampling
Non-probability sampling
1. Samping sistematis
2. Sampling kuota
3. Sampling aksidental
4. Purposive sampling
5. Sampling jenuh
6. Snowball sampling
Gambar 1. Skema Macam-macam Teknik Sampling
Jumlah sampel sering dinyatakan dengan ukuran sampel.
Apabila ukuran sampel makin mendekati populasi, maka
peluang kesalahan generalisasi semakin kecil, dan sebaliknya.

52. Nomogram Harry King
Terdapat berbagai cara yang dapat
digunakan
untuk
menghitung
besarnya sampel yang diperlukan
dalam penelitian. Salah satu cara
yang paling mudah adalah dengan
menggunakan Nomogram Harry
King. Cara menentukan ukuran
sampel
dengan
menggunakan
Nomogram ini didasarkan pada
asumsi bahwa populasi berdistribusi
normal. Sehingga apabila sampel
tidak
berdistribuasi
normal.
Sehinggga apabila sampel tidak
berdistribusi
normal
-misalnya
populasi homogen- maka Nomogram
tersebut tidak bisa dipakai. Berikut
ini ditampilkan Nomogram Harry
King.

53. Untuk menentukan ukuran sampel dari populasi dapat dipakai rumus Slovin
(1960) debagai berikut:
n
N
1 Ne 2
o n
=
ukuran sampel
o N
=
ukuran populasi
o e
=
nilai kritis (batas ketelitian) yang diinginkan
UKURAN SAMPEL UNTUK BATAS-BATAS KESALAHAN YANG
DITETAPKAN
Batas-batas kesalahan
Populasi
1%
2%
3%
4%
5%
10%
500
*
*
345
278
222
83
1.500
*
*
638
441
316
94
2.500
* 1.250
769
500
345
96
3.000
* 1.364
811
517
353
97
4.000
* 1.538
870
541
364
98
5.000
* 1.667
909
556
370
98
6.000
* 1.765
938
566
375
98
7.000
* 1.842
959
574
378
99
8.000
* 1.905
976
580
381
99
9.000
* 1.957
989
584
383
99
10.000
5.000
2.000
1.000
588
385
99

54. Penentuan Sampel dengan
Tabel Krecjie
• Tabel sampel berdasar Populasi dengan error
yang diijinkan 5%.

55. 7. Distribusi Normal
•
•
Distribusi normal dapat dipandang sebagai model atau dasar teori statistika
moderen
Distribusi normal adalah suatu model yang didefinisikan dengan rumus:
1
2
y
•
1 x
e 2
2
Dimana
y = ordinat grafik
x = skor yang diperoleh
rata2 populasi
simpangan baku populasi = 3,1416
e = 2,7183

56. • Distribusi normal berbentuk lonceng (bellshape) sehingga sering disebut bell shape
distribution. Model ini memiliki empat
karakteristik:
– Unimodal: satu modus
– Simetrik : distribusi sebelum dan sesudah
median sama
– Modus = Median = Mean
– Asimtotik : kurva distribusi tidak akan
menyentuh absisnya

57. Daerah dibawah kurva normal
• Luas daerah 0 ke z dapat diperoleh dengan:
1 2
z 1
x
e 2 dx
0 2
• Luas daerah dibawah normal dari 0 ke z ditabelkan

58. Pada pengukuran 200 subyek yang diambil secara
acak dari populasi N=1000 menghasilkan:
–
–
Mean sampel = 40
Simpangan baku = 10
1. Berapa persen subyek yang memperoleh skor
antara 40 dan 55?
2. Berapa persen subyek yang memperoleh skor
di atas 55?
3. Berapa persen subyek yang memperoleh skor
di bawah 35?
4. Berapa skor yang dicapai oleh mereka yang
tergolong 10% terbesar?

59. • 1. X=40  z=(40-40)/10=0,00
– X=55  z=(55-40)/10=1,5
– Lihat tabel distribusi normal:
• Antara 0,00 – 1,5  0,4332 =43,32%
• 43,32% x N = 433 orang
• 2. 0,5000 – 0,4332 = 0,0668
– 6,68% x N = 67 orang
• 3. X=35  z=(35-40)/10 = -0,5 ke 0
– Tabel didapat 0,1915
– Dibawah 35  0,5000 – 0,1915 = 0,3085 x N
• 4. 10%  ujung kanan
Setengah kurva 0,5000 – 0,1000 = 0,4000  z-1,28
Z = (X-Xm)/s
Didapat X = 53

60. Pada pengukuran IQ terhadap sampel 100 siswa
dari populasi 500 siswa menghasilkan:
–
–
Mean sampel = 120
Simpangan baku = 10
1. Berapa siswa yang IQ antara 120 dan 130?
2. Berapa jumlah siswa yg IQ diatas 130?
3. Berapa IQ mereka yg merupakan 5% siswa
tertinggi?

61. Tugas Matematika Terapan
• 1. Kumpulkan data sebanyak 50 buah kemudian
tentukan:
–
–
–
–
–
–
a. Rentang data
b. Banyak kelas dan panjang kelas
c. Daftar distribusi frekwensi
d. Grafik histogram
e. Grafik poligon
f. Grafik distribusi dalam %
• 2. Tentukan Mean, Median dan Modus data kelas
di atas. Berdasar hasilnya bagaimana tipe
distribusinya

62. • 3. Berdasar data sebelumnya tentukan ukuran
dispersinya dengan:
– Variasi (s2)
– Simpangan Baku (s)
– Koefisien variasi (kv)
• 4. Tentukan 8 data untuk x dan y yang memiliki
kecenderungan yang sama:
– Buat tabel dengan kolom x, y, x2, xy, y2
– Tentukan nilai intercept ( ) dan koefisien regresinya
( )
– Tentukan koefisien korelasinya (r)
– Bagaimana pendapat tentang hasil yang didapat

63. Referensi
• Furqon, ph.D. , 2001, Statistika terapan untuk
penelitian, ISBN 979-8433-13-0, CV Alfabeta,
Bandung, 230p
• Sugiono, 2002, Statistik Untuk Penelitian, ISBN 9798433-10-6, Alfabeta, Bandung, 306p.
• Sugiono, Dr. & Eri ibowo S.Pd., Statistika penelitian
dan Aplikasi dengan SPSS 10.0 for Window, ISBN
979-8433-50-3, CV Alfabeta, Bandung, 238p