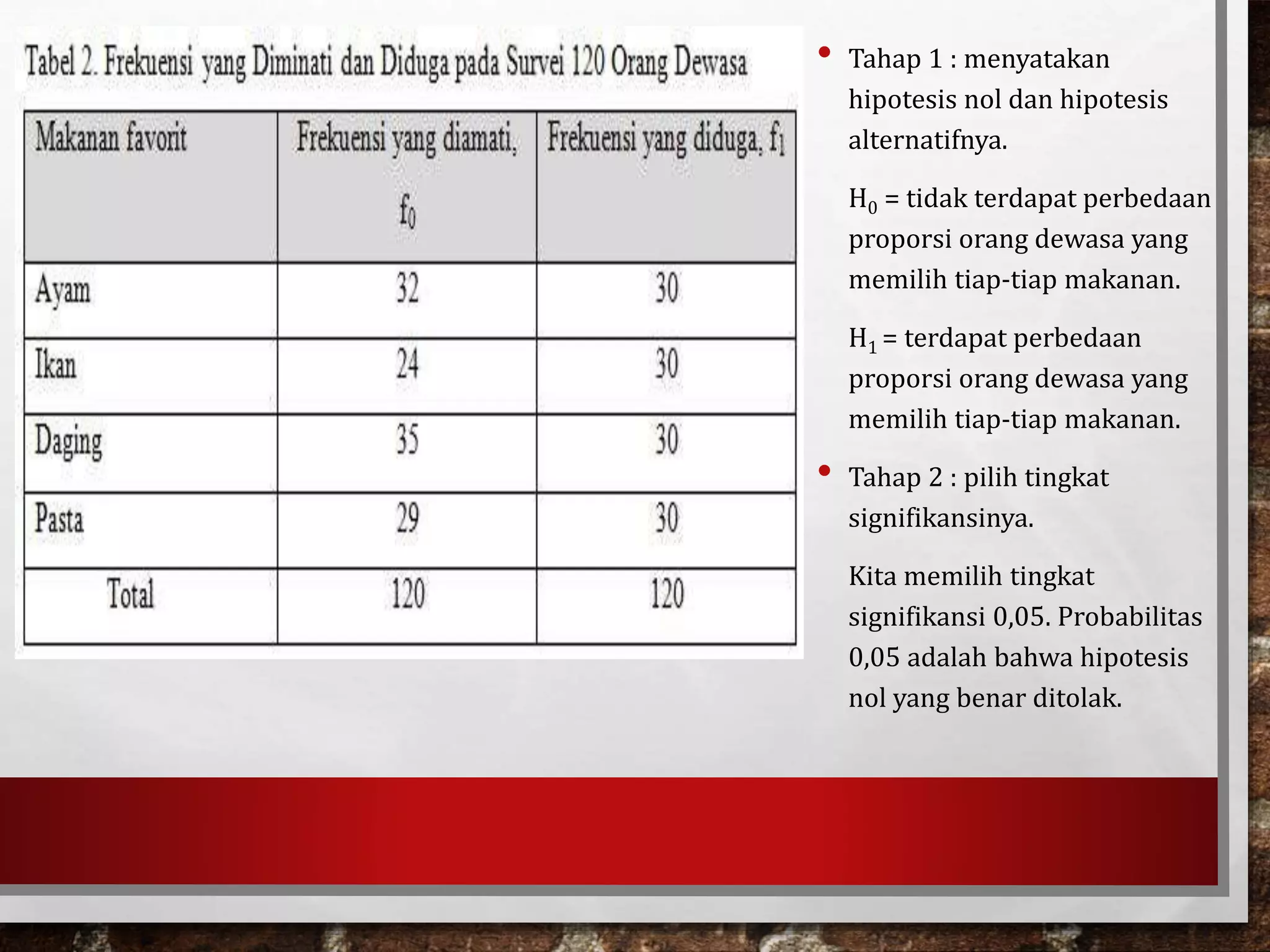
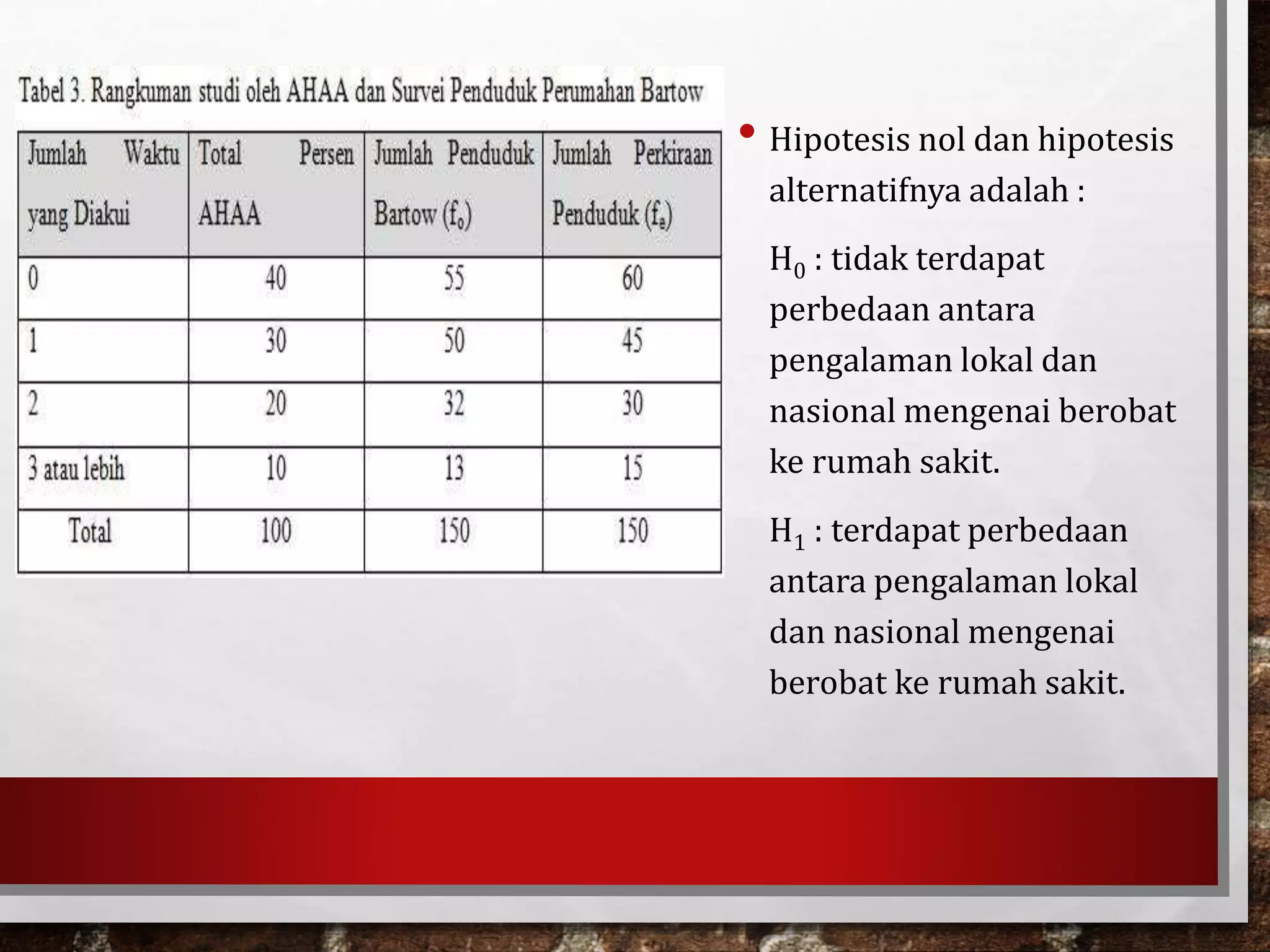
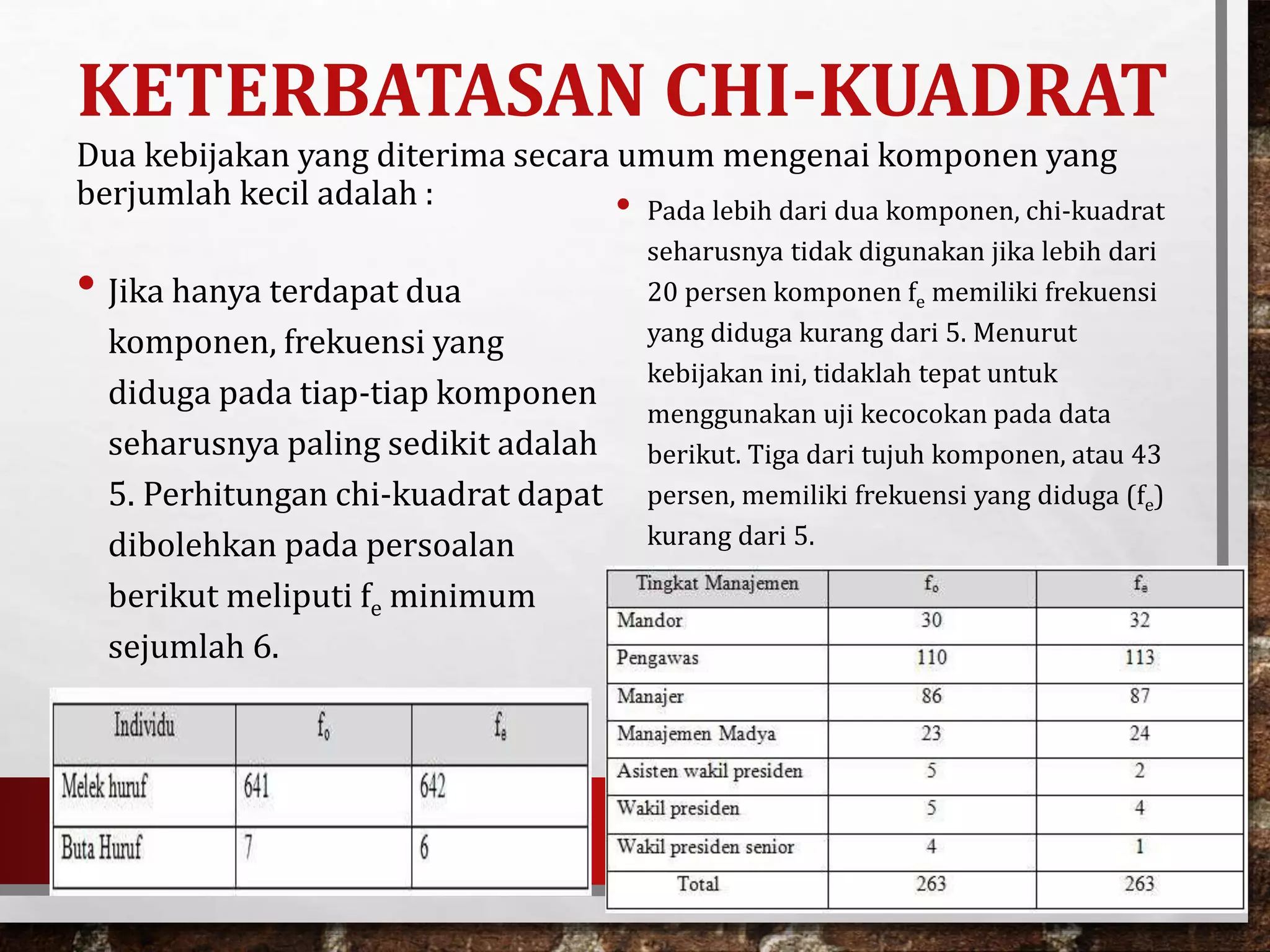
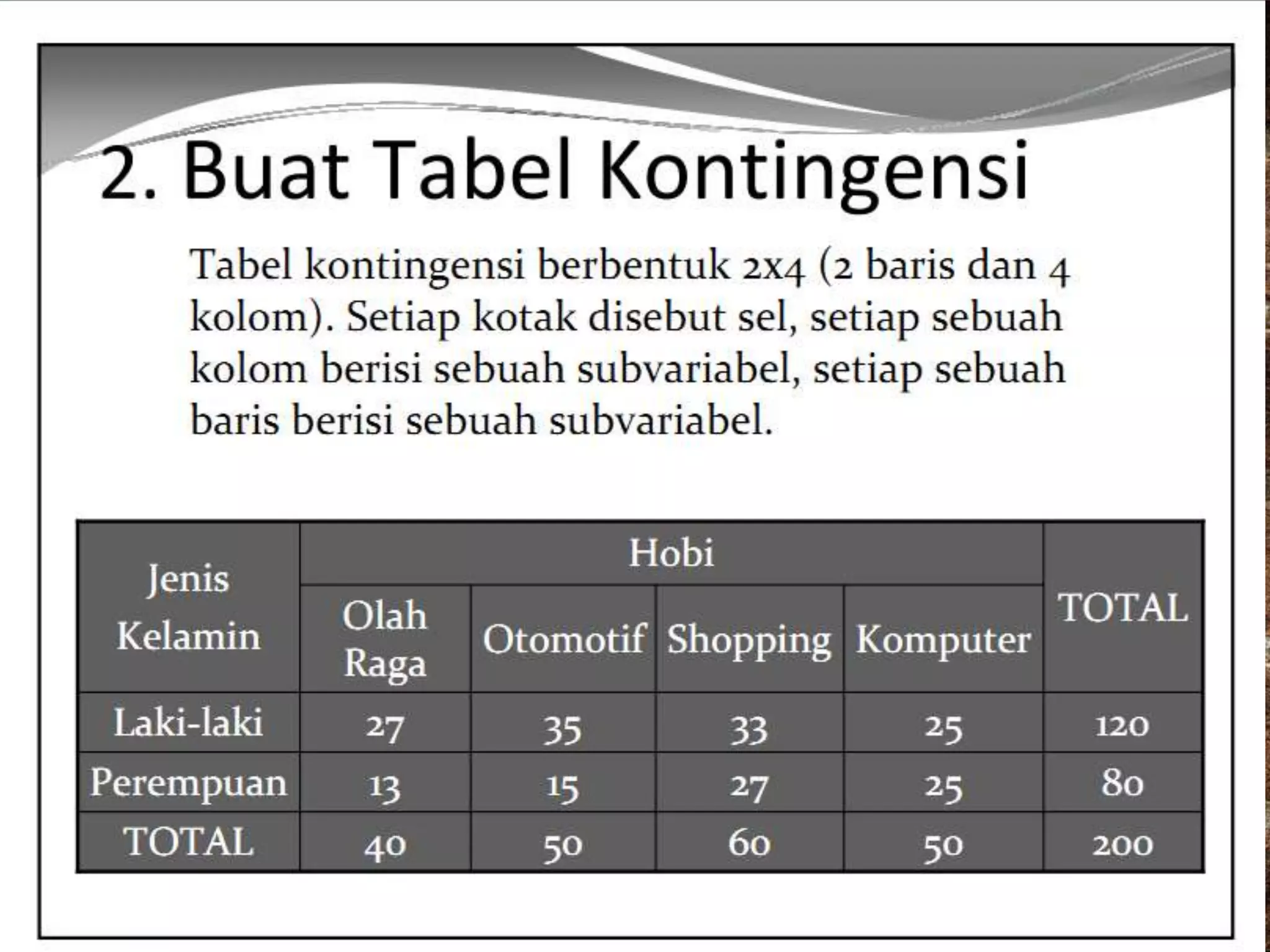
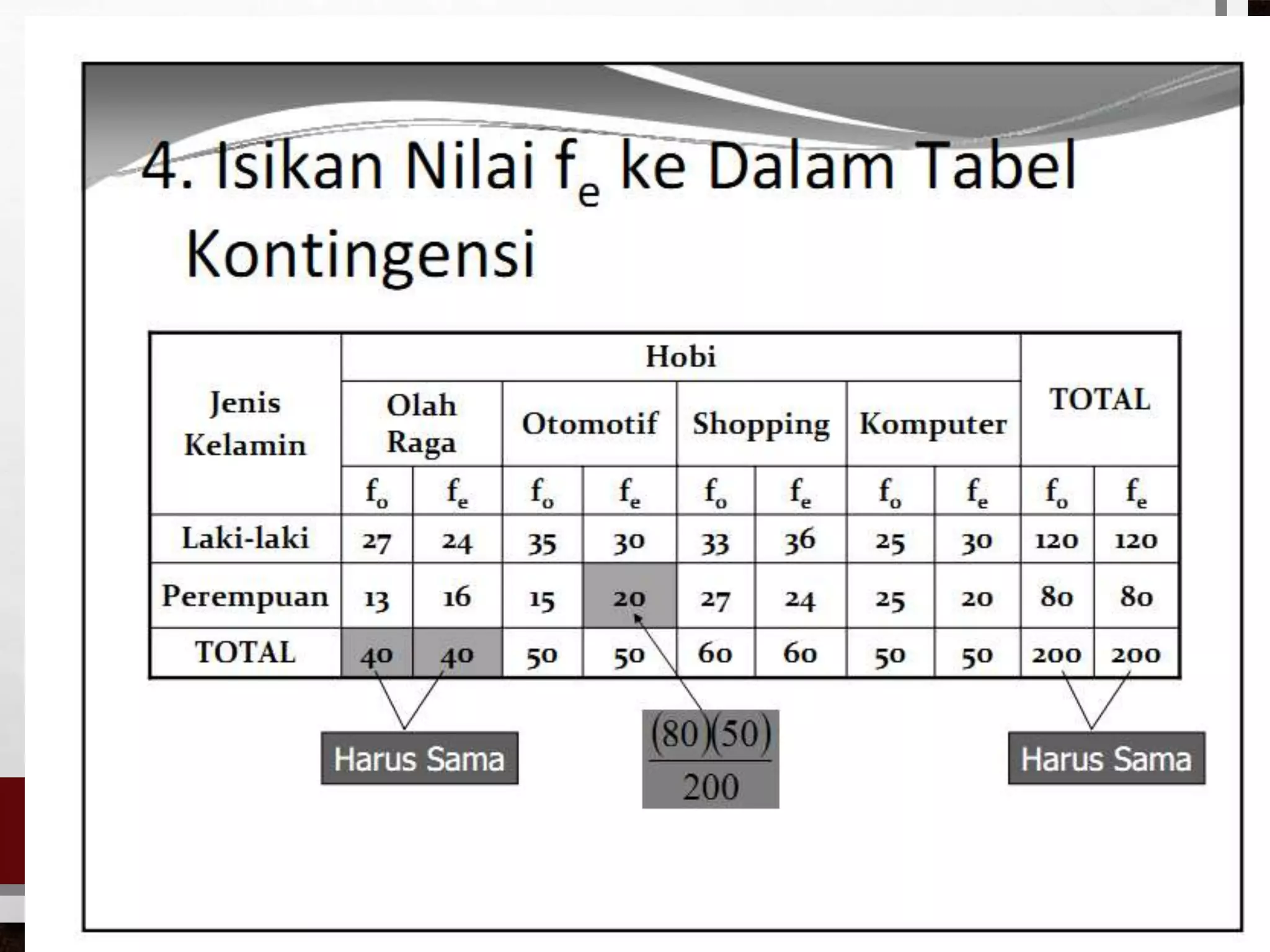
Dokumen ini membahas uji kecocokan menggunakan chi-square dan uji tanda dalam inferensi non-parametrik. Chi-square digunakan untuk membandingkan distribusi yang diamati dengan distribusi yang diharapkan, sementara uji tanda mengkaji selisih antara dua pengamatan yang berkaitan. Pentingnya pemilihan hipotesis dan penentuan nilai kritis dalam pengujian diuraikan untuk mencapai keputusan yang tepat.