Downloaded 108 times
Uploaded byShinta Alya
STATISTIKA EKONOMI Chi kuadrat
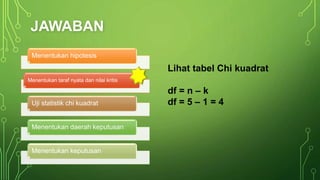
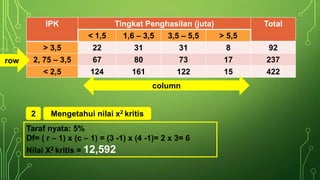
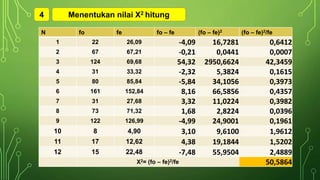
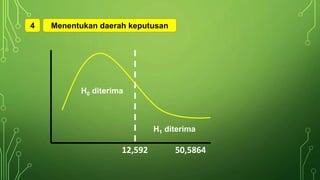
Dokumen ini membahas statistik nonparametrik, khususnya uji chi kuadrat, yang digunakan untuk analisis data tanpa asumsi distribusi. Terdapat penjelasan mengenai jenis skala data, contoh pengujian keselarasan, kenormalan, dan independensi menggunakan chi kuadrat, serta langkah-langkah dalam menghitung nilai-nilai yang diperlukan. Hasil akhir menunjukkan penerimaan hipotesis dalam beberapa uji yang dilakukan terkait data inflasi dan hubungan antara IPK dan tingkat penghasilan.
More Related Content
STATISTIKA EKONOMI Chi kuadrat
- 1. STATISTIK NONPARAMETRIK CHI KUADRAT SHINTA APRILIAWATI7101413225 UNIVERSITAS NEGERI SEMARANG
- 2. DEFINISI STATISTIK NONPARAMETRIK Statistik yang tidak memerlukan pembuatan asumsi tentang bentuk distribusi atau bebas distribusi, sehingga tidak memerlukan asumsi terhadap populasi yang akan diuji
- 3. MENGAPA MENGGUNAKAN STATISTIK NONPARAMETRIK? 1.Data nominal atau ordinal 2. Jumlah anggota populasi/sampel kecil 3. Distribusi data tidak normal
- 4. PERBEDAAN JENIS SKALADATA No Jenis Skala Definisi Contoh 1 Nominal Skala yang hanya merupakan penamaan/kode, tidak menyatakan lebih besar/lebih kecil Jenis kelamin Lokasi Jenis perbankan 2 Ordinal Skala yang berupa urutan lebih rendah/lebih tinggi Sangat baik Baik, cukup, kurang baik 3 Interval Skala yang bersifat numerik, namun tidak memiliki nilai nol mutlak IPK: 1,00; 2,00; 3,00; 4,00 4 Rasio Skala numerik dimana selisih setiap pengukuran adalah sama dan memiliki nilai nol mutlak Tinggi badan Berat badan Kecepatan
- 5. JENIS STATISTIK NONPARAMETRIK UJIDATA BERPERINGKAT UJI CHI KUADRAT
- 6. UJI CHI KUADRAT UjiChi Kuadrat untuk Keselarasan Uji Chi Kuadrat untuk Kenormalan Uji Chi Kuadrat untuk Independensi
- 7. UJI CHI KUADRATUNTUK KESELARASAN (GOODNESS OF FIT) • Uji keselarasan dengan frekuensi harapan sama Contoh Soal: Pemerintah menghendaki bahwa inflasi pada tahun 2014 sebesar 9,5% per tahun. Data di beberapa kota besar adalah sebagai berikut: Dengan data tersebut, tentukan apakah target atau harapan pemerintah masih sesuai dengan kondisi sebenarnya dengan taraf nyata 5%! Kota Inflasi (%) Jakarta 8,08 Bandung 10,97 Semarang 12,56 Surabaya 7,15 Denpasar 12,49
- 8. JAWABAN Ho : tidakada perbedaan antara nilai observasi dengan nilai harapan H1 : ada perbedaan antara nilai observasi dengan nilai harapan Menentukan hipotesis Menentukan taraf nyata dan nilai kritis Uji statistik chi kuadrat Menentukan daerah keputusan Menentukan keputusan
- 9. JAWABAN Lihat tabel Chikuadrat df = n – k df = 5 – 1 = 4 Menentukan hipotesis Menentukan taraf nyata dan nilai kritis Uji statistik chi kuadrat Menentukan daerah keputusan Menentukan keputusan
- 10. JAWABAN Menentukan hipotesis Menentukan tarafnyata dan nilai kritis Uji statistik chi kuadrat Menentukan daerah keputusan Menentukan keputusan fo fe fo – fe (fo – fe)2 (fo – fe)2/fe 8,08 9,5 -1,42 2,0164 0,2122 10,97 9,5 1,47 2,1609 0,2275 12,56 9,5 3,06 9,3636 0,9856 7,15 9,5 -2,35 5,5225 0,5813 12,49 9,5 2,99 8,9401 0,9411 X2= (fo – fe)2/fe 2,9477
- 11. JAWABAN Menentukan hipotesis Menentukan tarafnyata dan nilai kritis Uji statistik chi kuadrat Menentukan daerah keputusan Menentukan keputusan 9,488 H0 diterima H1 diterima 2,9477
- 12. • Uji keselarasandengan frekuensi harapan yang tidak sama Contoh Soal: Berikut adalah tabel harapan pemerintah mengenai tingkat inflasi di beberapa kota besar berikut realisasinya: UJI CHI KUADRAT UNTUK KESELARASAN (GOODNESS OF FIT) Kota Target Inflasi (%) Realisasi Inflasi (%) Jakarta 6,08 8,08 Bandung 9,97 10,97 Semarang 10,56 12,56 Surabaya 9,15 7,15 Denpasar 13,49 12,49 Dengan data tersebut, tentukan apakah target atau harapan pemerintah masih sesuai dengan kondisi sebenarnya dengan taraf nyata 5%!
- 13. Berikut adalah datasurvey jumlah jam belajar mandiri per minggu mahasiswa Fakultas Ekonomi, ujilah apakah data tersebut mengikuti distribusi normal! UJI CHI KUADRAT UNTUK KENORMALAN (UJI NORMALITAS) Interval Frekuensi (fo) Nilai Tengah (X) 0 – 4 9 2 5 – 9 10 7 10 – 14 11 12 15 – 19 7 17 20 - 24 3 22
- 14. Membuat distribusi frekuensi Menghitungrata2 hitung Menghitung standar deviasi Menentukan nilai Z Menentukan probabilitas kelas Menentukan nilai harapan Menentukan nilai chi kuadrat Menentukan Keputusan
- 15. Interval Frekuensi (fo) Nilai Tengah (X) fX X- 𝐗 (X - 𝐗)2 f(X - 𝐗)2 0 – 4 9 2 18 -8,125 66,016 594,144 5 – 9 10 7 70 -3,125 9,766 97,66 10 – 14 11 12 132 1,875 3,516 38,672 15 – 19 7 17 119 6,875 47,266 330,859 20 - 24 3 22 66 11,875 141,016 423,047 ∑fX 405 ∑f(X - 𝐗)2 1484,382 𝐗 = 405/ 40 10,125 S = ∑f(X − 𝐗)2 𝐧 −𝟏 6,169 MENGHITUNG RATA-RATA DAN STANDAR DEVIASI
- 16. MENENTUKAN NILAI ZUNTUK SETIAP KELAS (Z = (X - )/𝐒 )𝑿 Z0 = (0 – 10,125) / 6,169 = -1,64 Z4 = (4 – 10,125) / 6,169 = -0,99 Z5 = (5 – 10,125) / 6,169 = -0,83 Z9 = (9 – 10,125) / 6,169 = -0,18 Z10 = (10 – 10,125) / 6,169 = -0,02 Z14 = (14 – 10,125) / 6,169 = 0,63 Z15 = (15 – 10,125) / 6,169 = 0,79 Z19 = (19 – 10,125) / 6,169 = 1,44 Z20 = (20 – 10,125) / 6,169 = 1,60 Z24 = (24 – 10,125) / 6,169 = 2,25
- 17. MENENTUKAN NILAI ZUNTUK SETIAP KELAS (Z = (X - )/𝐒 )𝑿 Z0 = 0,4495 Z4 = 0,3389 0,1106 Z5 = 0,2967 Z9 = 0,0714 0,2253 Z10 = 0,0080 Z14 = 0,2357 0,2437 Z15 = 0,2852 Z19 = 0,4251 0,1399 Z20 = 0,4452 Z24 = 0,4878 0,0426
- 18. MENENTUKAN CHI KUADRAT foProbabilitas x n = fe (fo – fe) (fo – fe)2 (fo – fe)2/fe 9 0,1106 x 40 4,424 4,576 20,9398 4,7332 10 0,2253 x 40 9,012 0,988 0,9761 0,1083 11 0,2437 x 40 9,748 1,252 1,5675 0,1608 7 0,1399 x 40 5,596 1,404 1,9712 0,3522 3 0,0426 x 40 1,704 1,296 1,6796 0,9857 X2= (fo – fe)2/fe 6,3402 Nilai kritis = 9,488 Nilai chi kuadrat berada di area H0 diterima, maka terbukti bahwa data tersebut berdistribusi normal
- 19. Digunakan untuk mengetahuiapakah hubungan antara dua variabel Contoh Soal: Ada keyakinan bahwa apabila IPK tinggi, maka akan mendapatkan penghasilan tinggi. Berdasarkan keyakinan tersebut, perusahaan karir center tahun 2008 melakukan penelitian terhadap 751 sarjana dari berbagai perguruan tinggi yang bekerja di sektor perbankan di Jakarta. Berikut adalah hasilnya: UJI CHI KUADRAT UNTUK INDEPENDENSI
- 20. IPK Tingkat Penghasilan(juta) Total < 1,5 1,6 – 3,5 3,5 – 5,5 > 5,5 > 3,5 22 31 31 8 92 2, 75 – 3,5 67 80 73 17 237 < 2,5 124 161 122 15 422 Dari data tersebut, apakah keyakinan adanya hubungan antara IPK dengan tingkat penghasilan dapat dibenarkan? 1 Menyusun Hipotesis H0 : Tidak ada hubungan antara IPK dengan tingkat penghasilan H1 : Ada hubungan antara IPK dengan tingkat penghasilan
- 21. IPK Tingkat Penghasilan(juta) Total < 1,5 1,6 – 3,5 3,5 – 5,5 > 5,5 > 3,5 22 31 31 8 92 2, 75 – 3,5 67 80 73 17 237 < 2,5 124 161 122 15 422 2 Mengetahui nilai x2 kritis Taraf nyata: 5% Df= ( r – 1) x (c – 1) = (3 -1) x (4 -1)= 2 x 3= 6 Nilai X2 kritis = 12,592 row column
- 22. IPK Tingkat Penghasilan(juta) Total < 1,5 1,6 – 3,5 3,5 – 5,5 > 5,5 > 3,5 22 31 31 8 92 2, 75 – 3,5 67 80 73 17 237 < 2,5 124 161 122 15 422 Jumlah 213 272 226 40 751 3 Menentukan frekuensi harapan Fe = (jumlah menurut baris x jumlah menurut kolom) / jumlah total Fe22 = (213 x 92) / 751 = Fe67 = (213 x 237) / 751 =
- 23. 3 Memasukkan nilaifo dan fe dalam tabel kontingensi IPK Tingkat Penghasilan (juta) < 1,5 1,6 – 3,5 3,5 – 5,5 > 5,5 Fo Fe Fo Fe Fo Fe Fo Fe > 3,5 22 26,09 31 33,32 31 27,68 8 4,90 2, 75 – 3,5 67 67,21 80 85,84 73 71,32 17 12,62 < 2,5 124 69,68 161 152,84 122 126,99 15 22,48
- 24. 4 Menentukan nilaiX2 hitung N fo fe fo – fe (fo – fe)2 (fo – fe)2/fe 1 22 26,09 -4,09 16,7281 0,6412 2 67 67,21 -0,21 0,0441 0,0007 3 124 69,68 54,32 2950,6624 42,3459 4 31 33,32 -2,32 5,3824 0,1615 5 80 85,84 -5,84 34,1056 0,3973 6 161 152,84 8,16 66,5856 0,4357 7 31 27,68 3,32 11,0224 0,3982 8 73 71,32 1,68 2,8224 0,0396 9 122 126,99 -4,99 24,9001 0,1961 10 8 4,90 3,10 9,6100 1,9612 11 17 12,62 4,38 19,1844 1,5202 12 15 22,48 -7,48 55,9504 2,4889 X2= (fo – fe)2/fe 50,5864
- 25. 4 Menentukan daerahkeputusan 12,592 H0 diterima H1 diterima 50,5864
- 26.