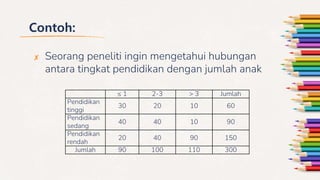
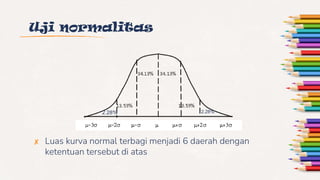
Dokumen ini membahas tentang uji chi-square, termasuk syarat penggunaannya, formulasi rumus, dan langkah-langkah pengujian untuk menentukan hubungan antara variabel kategori. Contoh-contoh di dalamnya menunjukkan cara menghitung dan menarik kesimpulan berdasarkan data yang diberikan dalam konteks minat beli, pendidikan, dan pendapat siswa. Selain itu, juga mencakup uji normalitas menggunakan chi-square untuk menentukan distribusi data.

1. UJI CHI-SQUARE

2. Syarat Chi - Square
✘ Variabel yang diuji adalah variabel katagorik
(data nominal atau ordinal)
✘ Bentuk kurva Chi - Square

3. Kegunaan Chi-Square
1. Independency Test (melihat hubungan atau
pengaruh dua variabel kategori )
2. Homogenity Test (homogenitas antar
kelompok)
3. Uji kenormalan data

4. Rumus
✘ Bila tabel kontingensi 2 x 2
✘ Bila tabel kontingensi selain 2 x 2
 




e
e
o
f
f
f
2
2 5
.
0

 



e
e
o
f
f
f 2
2

  



total
baris
o
kolom
o
f
f
f
- fo = frekuensi observasi
- fe = frekuensi ekspektasi
=
- derajat bebas (db)
= (r-1) (c-1)

5. Langkah Pengujian dengan Chi-Square
1. Menentukan hipotesis
2. Menentukan pengujian yang sesuai
3. Menentukan nilai tabel untuk 2
a (db)
4. Menentukan daerah keputusan
- Tolak H0 bila 2
hitung ≥ 2
a (db)
- Terima H0 bila 2
hitung < 2
a (db)
5. Menarik kesimpulan
5

6. Uji 2 Untuk Sample > 1 Kategori
✘ Seorang manager pemasaran ingin mengetahui
bagaimana minat pembelian suatu produk bila ditinjau
dari usia konsumen berdasarkan data berikut:
Minat
Usia
Suka Tidak
suka
Jumlah
Muda 10 30 40
Tua 40 20 60
Jumlah 50 50 100

7. Jawab:
• Menentukan hipotesis:
H0 : tidak terdapat hubungan antara minat beli
dengan usia konsumen
H1 : terdapat hubungan antara minat beli dengan
usia konsumen
• Menentukan nilai 2
hitung

8. Suka Tidak suka
Muda 40
Tua 60
50 50 100
       
0416
.
15
30
5
.
0
30
20
30
5
.
0
30
40
20
5
.
0
20
30
20
5
.
0
20
10
2
2
2
2
2














 Nilai tabel untuk 2
0.05 (1) =
Jawab:
10 30
40 20
20 20
30 30
3,841
 Menentukan daerah keputusan
Tolak H0 bila 2
hitung ≥ 2
0.05 (1)
Terima H0 bila 2
hitung < 2
0.05 (1)
 Sehingga kriteria keputusan adalah tolak H0 karena 15.0416 >
3.841 dengan kesimpulan bahwa ada hubungan antara minat
beli dengan usia konsumen
40 (50)
100
40 (50)
100
60 (50)
100
60 (50)
100

9. Contoh:
✘ Seorang peneliti ingin mengetahui hubungan
antara tingkat pendidikan dengan jumlah anak
≤ 1 2-3 > 3 Jumlah
Pendidikan
tinggi
30 20 10 60
Pendidikan
sedang
40 40 10 90
Pendidikan
rendah
20 40 90 150
Jumlah 90 100 110 300

10. Jawab:
1. Menentukan hipotesis:
Hipotesis:
H0 : tidak terdapat hubungan antara tingkat
pendidikan dengan jumlah anak
H1 : terdapat hubungan antara tingkat
pendidikan dengan jumlah anak

11. Jawab
✘ 2. Menentukan nilai 2
hitung
  



e
2
e
o
2
f
f
f

≤ 1 2-3 > 3 Jumlah
Pendidikan tinggi
60
Pendidikan
sedang
90
Pendidikan
rendah
150
Jumlah 90 100 110 300
30
40
20
20
40
40
10
10
90

12. Jawab:
3. Menentukan nilai tabel untuk 2
0.05 (4) =…..
4. Menentukan daerah keputusan
Tolak H0 bila 2
hitung ≥ 2
0.05 (4)
Terima H0 bila 2
hitung < 2
0.05 (4)
5. Sehingga kriteria keputusan adalah tolak H0
karena 2
hit > 2
0.05 (…) dengan kesimpulan
bahwa ada hubungan antara tingkat pendidikan
dengan jumlah anak.

13. Soal:
✘ Ujilah apakah ada hubungan antara minat acara
TV dengan kedua kelompok umur tersebut
Kelompok umur Minat Acara TV
Drama Musik Komedi
Dewasa 175 130 95
Remaja 125 120 105

14. Uji 2 untuk sample dengan 1 kategori
✘ Penelitian dilakukan terhadap 45 siswa sekolah kejuruan. 13
orang menyukai sekolah mereka, 8 orang menyatakan sama
saja dengan sekolah lain dan 14 anak tidak menyukai sekolah
mereka. Tentukanlah apakah terdapat perbedaan pendapat
antar siswa mengenai sekolah mereka
14
Pendapat
Frek
Menyukai Sama saja
Tdk
menyukai
Jumlah
fo
fe
13
15
18
15
14
15
45
45

15. Jawab :
1. Hipotesis:
✘ H0 : pendapat siswa mengenai sekolah mereka
sama
✘ H1 : pendapat siswa mengenai sekolah mereka
berbeda
2. menentukan uji yang sesuai
15
𝜒2
=
13 − 15 2
15
+
8 − 15 2
15
+
14 − 15 2
15
=

16. Jawab: (lanjutan)
3. Nilai tabel untuk 2
0.05 (2) =
4. Menentukan daerah keputusan
- Tolak H0 bila 2
hitung ≥ 2
0.05 (2)
- Terima H0 bila 2
hitung < 2
0.05 (2)
5. Sehingga kriteria keputusan adalah tolak H0 karena 2
hit > 2
0.05 (2) dengan kesimpulan bahwa terdapat perbedaan
pendapat antar siswa mengenai sekolah mereka
16

17. Soal
✘ PT jaya makmur mempunyai 5 unit usaha.
✘ Berdasarkan laporan, keuntungan yang diperoleh setiap
unit usaha adalah:
✘ Tentukan apakah kelima usaha tersebut memiliki
keuntungan yang sama atau berbeda
Bidang
usaha
Wartel Warnet
Toko
kelontong
FC kantin
Keuntungan 42 84 28 52 59

18. menghitung 2 tanpa frekuensi
harapan
✘ Persamaan yang digunakan
Kategori 1a Kategori 1b Jumlah baris
Kategori 2a a b a+b
Kategori 2b c d c+d
Jumlah kolom a+c b+d
Jml tot=
a+b+c+d
)
(
)
(
)
(
)
(
2
2
2
d
c
b
a
d
b
c
a
n
bc
ad
n















19. Latihan :
✘ Ujilah apakah ada hubungan antara minum es
buah dengan diare
Es Buah
Diare
Ada Tidak
Minum 20 18
Tidak minum 32 20

20. Uji normalitas
✘ Luas kurva normal terbagi menjadi 6 daerah dengan
ketentuan tersebut di atas
2.28%
2.28%

21. Latihan
✘ berikut ini adalah 50 data produksi gabah di suatu
daerah. Tentukan apakah data tersebut berdistribusi
normal
21
20 24 26 30 38
20 24 27 31 38
20 25 27 31 38
22 25 28 33 39
22 25 28 33 40
22 25 30 34 40
22 25 30 35 40
23 25 30 35 43
24 26 30 36 43
24 26 30 37 44
Berdasarkan hasil perhitungan
diperoleh:
mean= 29.9
standard deviasi = 6.8
CARA: Lihat materi statistika 1

22. Jawab:
• Langkah-langkah uji normalitas dengan 2
1. Tentukan hipotesisnya:
H0: data berdistribusi normal
H1 : data tidak berdistribusi normal
2. Menentukan nilai 2
a. mencari nilai mean dan standard deviasi
b. menentukan nilai interval untuk mendapatkan
frekuensi observasi (fo)

23. Jawab: (lanjutan)
3. Membuat tabel untuk menghitung nilai 2
Kategori Interval fo fo (%) fe (%) fo-fe (fo-fe)2
<Mean-2s < 16.3 0 0 2.28 -2.28 5.1984 2.28
Mean-2s s/d mean-1s 16.3-23.1 8 16 13.59 2.41 5.8081 0.43
Mean-1s s/d mean 23.1-29.9 17 34 34.13 -0.13 0.0169 0.00
mean s/d mean+1s 29.9-36.7 14 28 34.13 -6.13 37.5769 1.10
Mean+1s s/d mean+2s 36.7-43.5 10 20 13.59 6.41 41.088 3.02
Mean+2s < 43.5 < 1 2 2.28 -0.28 0.0784 0.03
Jumlah 50 100 100 6.87
 
e
e
o
f
f
f
2

Kategori: menyesuaikan dengan pembagian daerah kurva normal sehingga selalu terdiri dari 6 kategori
Interval: nilainya tergantung dari mean dan std deviasi data (subtitusikan ke persamaan kategori)
f0 : sesuaikan antara data soal dengan interval
fe (%) : sesuai dengan persentase daerah pada kurva normal

24. Jawab: (lanjutan)
4. Menentukan nilai 2 tabel
2 tabel untuk db=5 dan taraf nyata 5% = 11.07
5. Menentukan kesimpulan
Karena 2 hitung (=6.87) lebih kecil daripada 2
tabel (11.07) maka terima H0 dengan
kesimpulan bahwa data berdistribusi normal