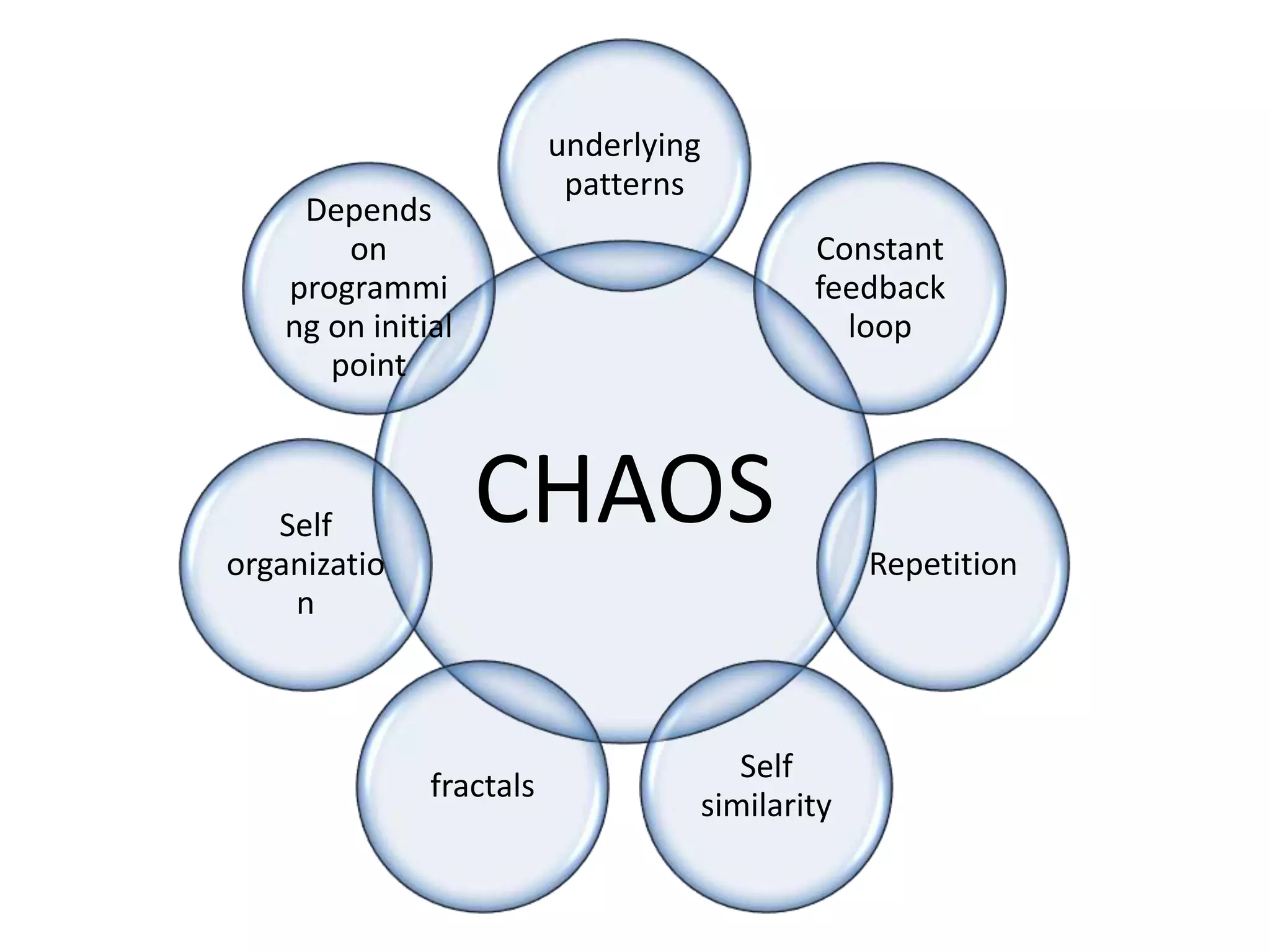
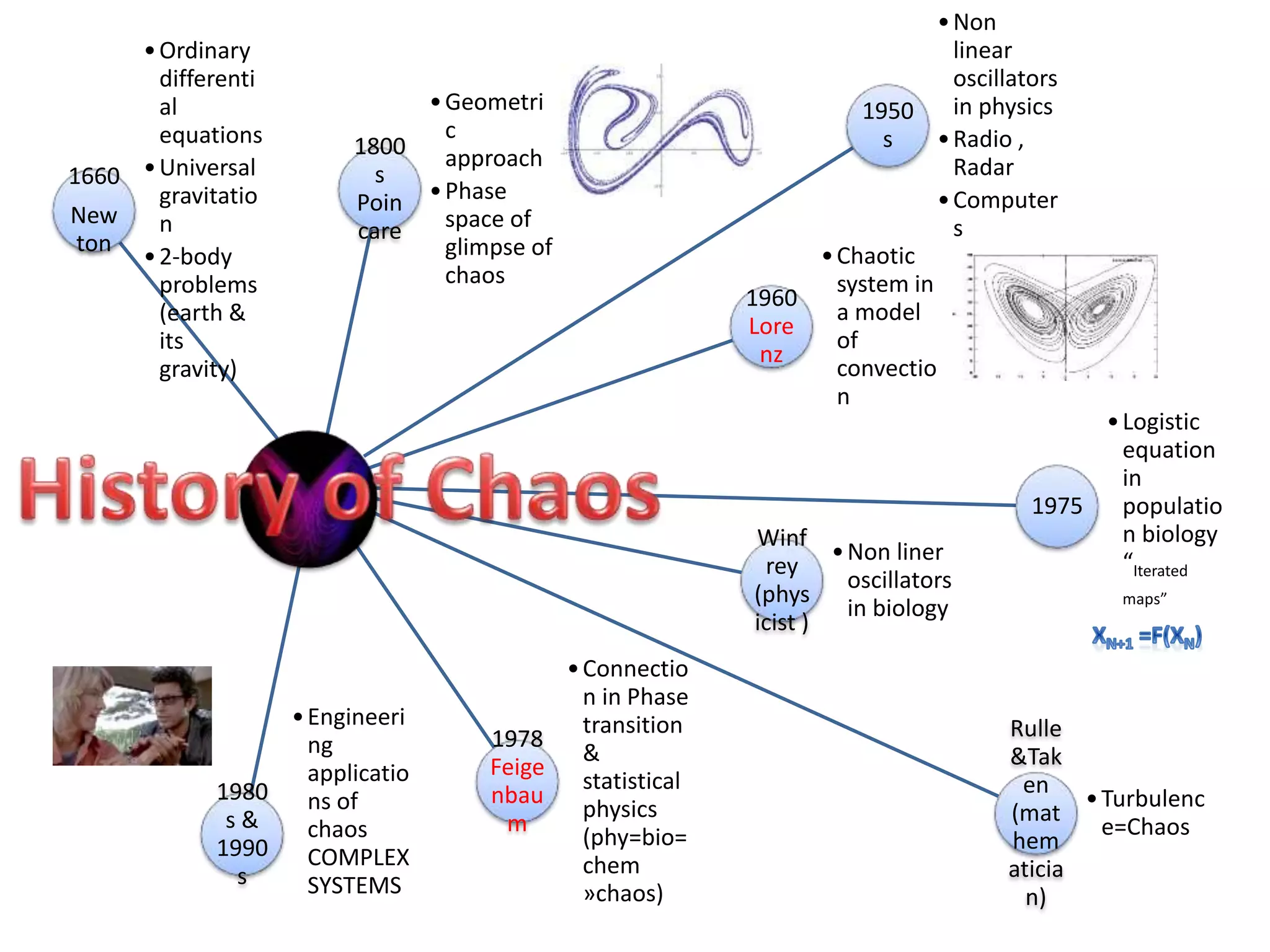
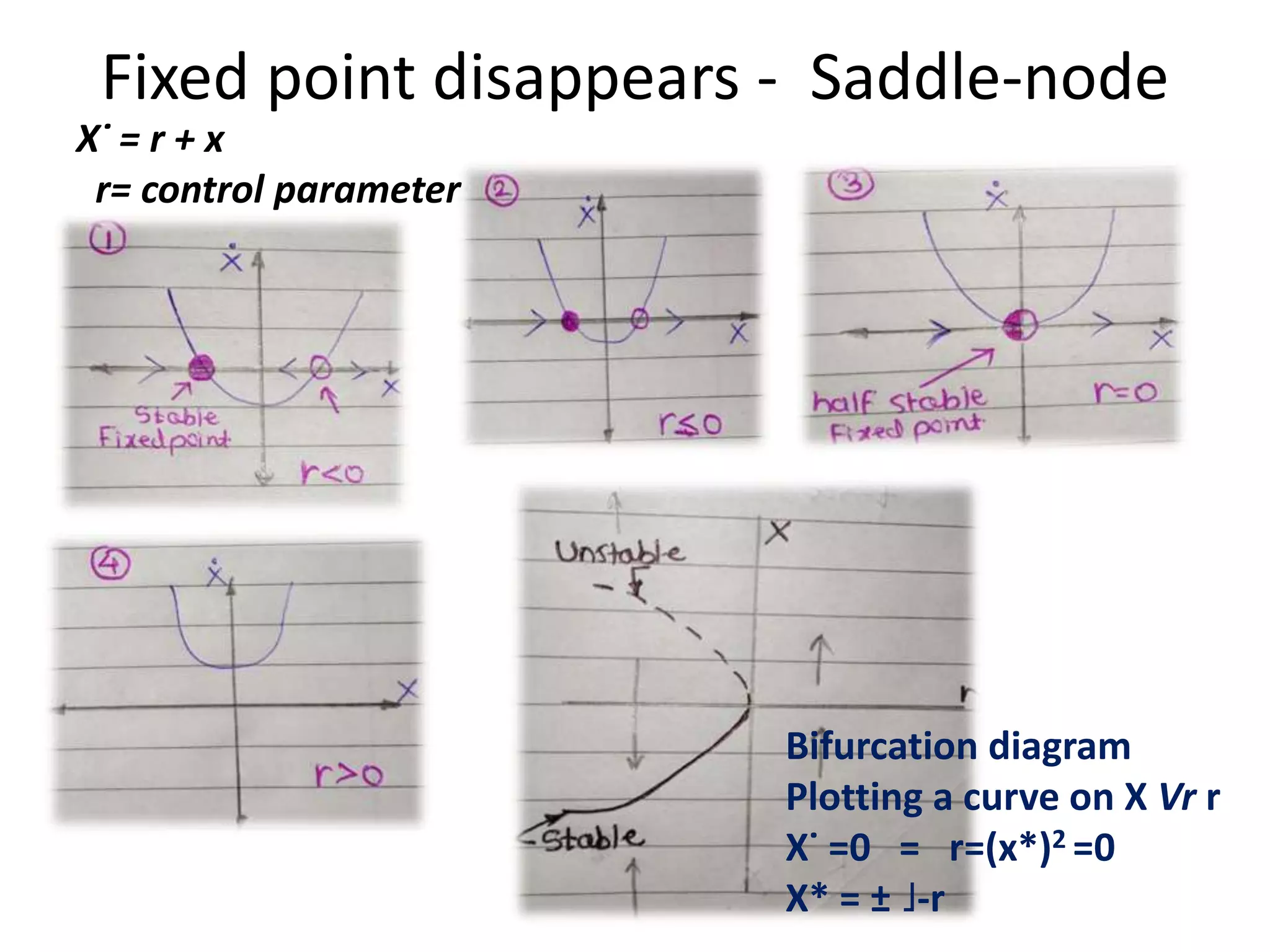
This document discusses nonlinear dynamics and chaos. It begins with an overview of key concepts in chaos like fractals, self-similarity, and dependence on initial conditions. It then provides a brief history of the field, covering contributions from Newton, Poincare, Lorentz, and others. The document proceeds to discuss logistic equations and bifurcations. It provides examples of fixed points, phase portraits, and bifurcation diagrams. It also covers modeling population dynamics and insect outbreaks using logistic growth equations.

1. Non Linear Dynamics & Chaos
Presented By – Anupama K.
Prof. Storgatz Cornell University

2. CHAOS
underlying
patterns
Constant
feedback
loop
Repetition
Self
similarity
fractals
Self
organizatio
n
Depends
on
programmi
ng on initial
point

3. 1660
New
ton
•Ordinary
differenti
al
equations
•Universal
gravitatio
n
•2-body
problems
(earth &
its
gravity)
1800
s
Poin
care
•Geometri
c
approach
•Phase
space of
glimpse of
chaos
1950
s
•Non
linear
oscillators
in physics
•Radio ,
Radar
•Computer
s
1960
Lore
nz
•Chaotic
system in
a model
of
convectio
n
1975
•Logistic
equation
in
populatio
n biology
“Iterated
maps”
Winf
rey
(phys
icist )
•Non liner
oscillators
in biology
Rulle
&Tak
en
(mat
hem
aticia
n)
•Turbulenc
e=Chaos
1978
Feige
nbau
m
•Connectio
n in Phase
transition
&
statistical
physics
(phy=bio=
chem
»chaos)
1980
s &
1990
s
•Engineeri
ng
applicatio
ns of
chaos
COMPLEX
SYSTEMS

4. Logistic structure of dynamics
• Differential equation X˙ =f(X̲)
• X̲ Є Ɽn X̲=(x1,….,xn)
• The system depends on only xi & not on time,
then the system is autonomous .
Helps – visualizing the phase space for geometric
systems
• In components , X˙1= f1 (X1,…..,Xn)
:
X˙n= fn(X1,…..,Xn)
t˙= 1 Continued…

5. • Ex . Simple harmonic oscillator
m ẍ + k x = 0 (convert ẍ in 1st order eqn)
x˙ = f ( x )
Let x1= x , x2=x˙
x˙1 = x2 , linear 2nd order
x˙2 = - kx1 / m system
• Pendulum ẍ + sin x = 0
x˙1=x2 non liner, 2ndorder
x˙2=sin x1 system

6. Analytical Solution of ODE !
• Phase Portrait – picture of all quantitatively
different trajectories.
• Geometric representation of the trajectories of
a dynamical system in the phase plane. Each set
of initial conditions is represented by a different
curve, or point.

7. Governing
equation
variables No.
(n=) ›
n=1 n=2 n=3 n=∞
Linear system RC circuit Simple
harmonic
motion
- Maxwell’s
equation
(application-
communicatio
n system )
Non-linear
system
Logistic
growth of
population
Pendulum Lorenz
equation for
topographic
regions i.e.
CHAOS
General
Relativity
turbulence
(complex
system
network)

8. • X˙= f (x) ; x Є Ɽ
• X˙=sin x For 1st order Non-linear
• Formula ⌠dx/ sinx =⌠ dt = t+c
• ⌠ cosec x dx = ln │cosec x + cot x │
• Initial condition x = x0 at t=0
→ t = ln │cosec x0+ cot x0 / cosec x + cot x │

9. • Ex. - If x0 = π/4, limt͢ ∞ x(t) =?
• velocity=X˙=0 at fixed point (Notation- X*)
• X = position of imaginary particle

10. Logistic equation in population biology
• X˙ = r.(1-X/K)
X = population size
X ˙ = growth rate

11. • At X˙= f (x) ; x Є Ɽ
• X =imaginary particle
• X*= fixed point
Lecture 2……
Figure for examine the linearization

12. Linearization
• Let x(t)= x* + ɳ (t) , where │ɳ│<<1
• x˙= (x*+ ɳ)˙= ɳ˙
‖
f(x)=f(x*+ ɳ)= f (x*)+ɳ. f’(x*)+ɳ2/2. f’(x*)+…….
X*=fixed point: consider f(x*)as number
If f(x*) ‡0,the term │f(x*+ ɳ)│>> │ɳ2/2.f’(x*)│
Examine dynamic chaos to a fixed point x*

13. • Neglecting order of ɳ2 yield linearization of system at
x*
• ɳ˙=r ɳ where r=f’(x*)
• Exponential growth ɳ=ɳ0 ert if r>0
Decay if r<0
We can notice that–on graph +ve slope
(i.e. point is stable )
But also analytically unstable !
No information from linearization if f’(x*)=0

14. • X*=0 is a fixed point for all these
• f’(x*)=f’(0)=0 in each case
Examples :

15. Ex. Logistic equation
X ˙= r x(1- x/k)
• f’(x)= r-( 2rx/k)
r = growth rate
k = carrying capacity
x = population of organisms
When 1) x* =0
f’(0)= r>0
X*=0
Unstable
2) x*=k
f’(k)=r-(2rk/k)=-r<0
So X*=k
Stable

16. Existence and uniqueness
• Solution to X˙= f(x) exist
• Are unique if f(x)and f’(x) are continuous
• F is continuously differentiable
Solutions of differentiable equations exist around
very tiny time around time equals to “zero”

17. Impossibility of oscillations
• What is possible behavior of x(t)as t͢→∞, for
X˙=f(x) ?
1. X(t)→±∞ as t→∞ or
2. X(t)→X*
Impossible to have Time Series or Periodic System
Reason : All trajectories x(t) increases or decreases
monotonically or stay fixed.
Oscillation, periodic solution,
damped oscillation is not
possible

18. Bifercation
• As a parameters changes qualitative structure
of the vector field may changes dramatically .
dx/dt = f (x,r)
• dynamic system will have some specific
dynamic behavior, if “r” changes dynamic
behavior of system may change drastically –
this transmission point is called a bifurcation

19. Fixed point disappears - Saddle-node
Bifurcation diagram
Plotting a curve on X Vr r
X˙ =0 = r=(x*)2 =0
X* = ± ˩-r
X˙ = r + x
r= control parameter

20. Fixed point collide - Transcritical
• Normal form X˙= rx –x2 =x(r-x)
• X *=0 , X*= r
• Note :- X*=0 is a fixed point for all r – can’t be
distorted but its stability can change
• f’(x)= d/dx (rx-x2) = r-2x
f’(0)= r
X*= 0 stable (r<0)
unstable (r>0)
f’(r)= r-2r = -r

21. New fixed point emerge – Pitchfork
• Occurs in system with symmetry
• X˙ = rx – x3 has symmetry x →-x
Bifurcating
solutions are
stable

22. Over Damped Bead On A Rotating
Hoop

23. Particle is moving in a circle &
we want to keep it moving in a
circle of radius ρ
having a force from the center
strength m times the velocity
square divide by radius ρ
(m(ρω)2)/ ρ
= mρω2
This whole apparatus (hoop & controller) making its spin
in big bucket of honey and where at initial time the
particle is somewhere but we giving tremendous viscosity
initially.. It got big initial velocity but remember its honey
so it doesn't going quickly damped out & then it will start
like we see in the picture

24. • Newton’s law F= ma
• m r φ¨ = - brφ˙ - mg
sinφ + mρω2cosφ
b = property of fluid & bead
only
b will be proportional to
viscosity
• (m(ρω)2)/ ρ = mρω2
Viscous
damping
Gravity term Centrifugal term
m r φ¨ = - brφ˙ - mg sinφ + mrω2sinφ cosφ

25. Phase Portrait Diagram
• Eq n having φ¨(double derivative) & sinφ cosφ
(non linear functions)
• Acceleration is tiny term compared to the right
side term
• suppose m r φ¨ is negligible (in some case) then
brφ˙= mg sinφ ((rω2/g)cosφ-1))
• Fixed point – satisfy either sinφ*=0 or
cosφ*=(g/(rω2))
• sinφ*=0 when φ*= 0 (bottom) or π (top)
• φ*= π i.e. bead at top , can’t possible to be stable
point !

26. • Fixed point - cosφ*=(g/(rω2)) solution for φ*
exist if g ≤ (rω2)
• Put γ =((rω2)/g) (dimensionless)
• Then cosφ*=(1/ γ) never hit the case(1/ γ)>1
Phase Portrait:
γ>1 Fast spin
γ,<1
slow spin
We get exit pair of fixed points
±φ*=0 when (1/γ) =1
Bifurcation diagram
Maximum value of cos φ is 1

27. When Can We Neglect mrφ¨ ?
• If m=0 centrifugal & gravity terms become zero
too!
• mrφ¨ = -brφ˙+ mg sinφ (γ cosφ-1)
• Use dimensional analysis : suppose T=
characteristics time scale on which bead changes
its position significantly
• Such that φ˙≈(1/T) and φ¨≈(1/T2) (T will be chosen latter)
• Reduce the number: let Ԏ= dimensionless time &
proportional to ordinary time (t/T)
• By chain rule: dφ/dt = (dφ/dԎ)(dԎ/dt)
→(1/T)(dφ/dԎ)
• (1/T) (dφ/dԎ)will remain order of 1 as m→0, if
‘T’ chosen correctly.
mrφ¨ = -brφ˙+ mg sinφ ((rω2/g)cosφ-1))

28. • Now we transform 1st order derivative into new
independent variable the second derivative i.e.
angular acceleration
• Chain rule – (d2/dt2) =(1/T2)(d2φ/dԎ2)
• φ¨= (1/T2) φ’’
• Governing equation becomes
• ((mr)/T2)φ”= - ((br)/T)φ’ + mg sinφ (γcosφ-1)
• Divide out “mg”
• {r/(gT2)}φ” = {-br/(mgT)}φ’ + f (φ)
Let φ’=dφ/dԎ
(dimensionless
time derivative)
Remove all unit of force by dividing through a typical
force ‘mg’ to make equation dimensionless
F(φ)= sinφ(γcosφ-1)

29. • If we consider φ’’& φ’ are order of 1 objects in
magnitude .consider some limit , ether viscosity
going to be infinity or mass going to zero, remain
kind of on the order of one
• Consider f(φ) is order of 1
• φ’, φ”,f ~ order of 1
• Aim : neglect the acceleration term
• {r/(gT2)}φ” = {-br/(mgT)}φ’ + f (φ)
• We want scaling to choose T such that {br/mgT}~
order of 1
• Choose T={br/mg}
• Then (r/gT2)={r/[g(br/mg)2]} = (rm2g2/gb2r2)
• (m2g/b2r)<<1 (giving notation ϵ)
But (r/gT2)<<1

30. • m 2<<< (b2r/g)
• The bead is much smaller than its mass , that
means small & then we can neglect the inertia
term or another way if the viscosity is very high.
• stokes flow ,Reynolds number flow that valid
when viscosity is very high then we can neglect
the inertial forces compared to damping forces
• Viscosity limit is when this should be valid
• ϵφ”= - φ’+f (φ)
• A singular limit : as ϵ =(m2g/b2 r)→0
• we loose the highest order derivative (ϵφ”) then
can’t satisfy both initial velocity & initial position ,
even when ϵ<<1 our approach is only valid after a
rapid initial transient

31. • That transient requires a different time scale
ϵφ”+φ’= f (φ)
• If we want to analyze that 2 dimensional system
then correct way of doing it as opposite to our 1 D
approximation we need another variable
• So let called it Ω(dimensionless) angular velocity
Let Ω= Φ’
Ω’=Φ”=(1/ϵ) {f(Φ)-Ω)
So on phase plans as opposite the phase lines : Ω &
φ
So our scaling fails (choice of ‘T’ during this initial time
[problem with 2 time scales i.e. very fast timescale at
beginning during which system tries to accommodate
initial position & velocity)then, but correct after that

32. Just Draw A Curve
• This whole apparatus (hoop & controller) making its spin in big bucket of honey
and where at initial time the particle is somewhere but we giving tremendous
viscosity initially.. It got big initial velocity but remember its honey so it doesn't
going quickly damped out & then it will start like we see in the picture
We have value of˙Ω i.e.φ’
have a component of velocity
looks like this
Ω’ component of
velocity (these
expression will be
negative because
Ω>f(φ) where above
the curve so this is
negative )
If above the curve it goes
fast straight up

33. Model of an insect outbreak
• Bifurcation problem: it involves 2 different
parameters& jumps .( Ludwig (1978) journal
Animal ecology 43.315)
• Spruce budworms ( found on Canadian timber)
can defoliate forest in 4 years
• N(t) = population of budworms
• N˙= RN {1-(N/K)} – P(N)
Logistic growth Death due to predators (birds)
P(N) = {BN2/A2+N2}

34. • P(N) = {BN2/A2+N2}
• X ˙= rx{1-(x/k)}
• Four parameters A,B,R,K
• Characteristics population sizes – A,K
• Choose scale of “N” to make the nonlinear P(N). Because
P(N)looking more nonlinear
• Let X= N/A
Eqn - N˙= RN {1-(N/K)} – P(N) becomes
• A(dx/dt) = RAX{1-(AX/K)}-{BA2X2/A2(1+X2)}
• (A/B) (dx/dt) = {R(AX/B){1-(AX/K)}} -{X2/(1+X2)}
• Let Ԏ= (Bt/A) (dimensionless time)
• X’ = rX[1-(X/K)] – (X2/1+X2)
r = growth rate
K= carrying capacity
X= population of organisms
N= AX
N˙= AX˙
Divide by B
We introduce hear dimensionless time
‘ = d/dԎ
Buckingham π theorem:
reduce 4 parameters to
2 dimensionless
parameters

35. • Fixed points X’=0
• Other X*= satisfy r{1-(X/K)} = {X/(1+X2)}
‘a’ type roots :low level of budworms That picture occurs when the line
is shallow
For K ,we can have 1,2, or 3
intersections . As ‘r’ increases
When from
1→ 2 → 3→ 2→ 1
a a,bc a,b,c ab,c c

36. Bifurcation occurs at certain (r,k) pairs
Suppose 3 fixed points besides X*= 0

37. can get jump phenomenon after a
saddle node : suppose ‘X’ is at ‘a’ (i.e.
population at low level ) & parameter
starts drift
A= level of total population of budworms
“A” is proportional to surface area of foliage
A’= critical density of budworms per leaf
S← no of leave
We can visualize this
as “cusp catastrophe”
surface
As the forest ages “r” increases slowly
r = (RA/B)

38. Two Dimensional System
Phase plane analysis for
X˙=f (x,y)
Y˙= g(x,y)
(x,y) ϵ Ɽ2 (x˙,y˙)
A vector field on phase plane
f & g are nonlinear
functions
Gives us picture of trajectory phase point moving on
phase plane
Where X̲ = (x y)
Vector version of X̲˙ = f(x)
X̲ ϵ Ɽ2

39. If f̲ is continuously differentiable , then solution X̲ (t) exist and
are unique for initial condition
(so we don’t have to think about existence & uniqueness that will come
automatically)
Following the local arrows as solution to the
differential equation will look like that we’re
calling a trajectory
The vector field is interpretation of the differential
equation i.e. X˙& Y˙ are functions of x & y plane
The trajectory is the analog of the solution of the
equation with every point on the trajectory
The local vector defined by the vector field will be tangent
to the trajectory (follows the arrow )

40. Implication Of Uniqueness
Trajectories can’t cross
Reason : If we concentrate on the crossing
point then heave 2 impossible future starting
at point of intersection & going to 2 ways that
violetes uniqueness of solution
(Proof by the existence & uniqueness for differential
equation)
Trajectories can approach the same fixed point
Reason : there is no contradiction as there is
fixed point so you just start there other
trajectories don’t actually touch the fixed point.
They just approaching it.
(Might be at infinity times yes they would touch but at
finite times they don’t )
Fixed point: (x,y) where X˙=0 & Y˙=0
F(X*)= 0

41. Strong topological consequences of no crossing
trajectories : in Ɽ2
Closed orbit trajectory
Periodic solution of
differential equation
or a repeating
motion of the system
Geometric
counterpart of some
periodic behavior
This can never get
inside a closed orbit
Other
trajectories
can’t get inside
because no
way to getting
in without
crossing
This orbit will
eventually close to
form another closed
orbit or will spiral out
to the original orbit .if
there are fixed point
inside it might
approach a fixed point
(called the Poincare &
Dixon theorem )

42. Reference
• Nonlinear Dynamics and Chaos - Steven Strogatz,
Cornell University