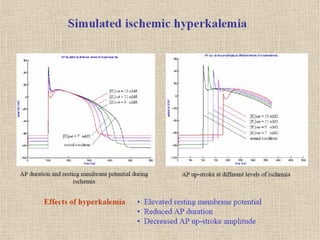
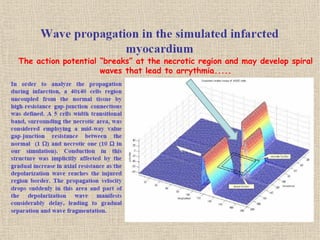
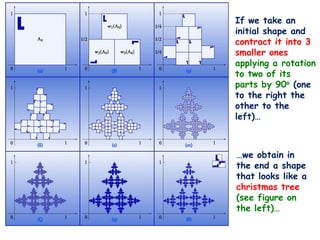
The document discusses the concept of complexity in large systems characterized by nonlinear interactions and emergent behaviors, emphasizing the role of mathematics in understanding these phenomena across various scientific fields. It highlights how fractal geometry and chaos theory can model complex structures like trees and population dynamics, and how self-organization leads to patterns in nature and society. The lecture concludes by advocating for the use of mathematical modeling as a tool to study and predict behaviors in complex physical, biological, and social systems.

1. Tassos Bountis
Department of Mathematics and Center for Research
and Applications of Nonlinear Systems
http://www.math.upatras.gr/~crans
University of Patras, Patras GREECE
Lecture at the OUT OF THE BOX Conference
Maribor, Slovenia, May 15-17,2012

2. What is Complexity?
At the beginning of 21st century we have understood
that:
• Complexity, is a property of large systems, consisting
of a huge number of units, involving nonlinearly
interacting agents, which can exhibit incredibly complex
behavior.
• New structures can emerge out of non-equilibrium and
order can be born out of chaos, following a process
called self-organization. Complex systems in the
Natural, Life and Social Sciences produce new shapes,
patterns and forms that cannot be understood by
studying only their individual parts.

3. Mathematics has already been quite helpful:
• The Theory of Chaos explores the unpredictable time evolution of
nonlinear dynamical systems like the weather, the electro-
cardiogram and encephalogram, mechanical, chemical and electrical
oscillations, seismic activity and even stock market fluctuations.
• The Geometry of Fractals analyzes the complex spatial structure
of trees and rocks, the dendritic shape of the bronchial “tree” in
the lungs, the cardiac muscle network and the blood circulatory
system.
• Most importantly, we can construct appropriate mathematical
models that: (a) reproduce the main features of a complex system
and (b) provide invaluable insight in revealing some of its
fundamental properties.

4. Some of the main questions we face today in what is
called Complexity Science are:
• How do we use Mathematics to observe, measure and
understand complex phenomena in the Natural, Life and
Social Sciences?
• Should we only look for universal principles and laws
expressed by mathematical formulas to understand atoms,
molecules, cells, trees, forests, living organisms and
ultimately society?
• How can use our perception and intuition to try to construct
suitable mathematical models that will help us shed some
light on the remarkably complex phenomena we observe
around us?

5. What is a tree?
• Is it what an artist would perceive?
like Mondrian (1872-1944) or van Gogh( 1853-1890)?

6. ......or what a biologist would study?
What is it that impresses us first about a tree?

7. Could it be a kind of self-
similarity in the way two of its
branches bifurcate out of a
bigger branch so that they are
smaller by a scaling factor?
Observe that besides shortening
the branches at every bifurcation,
we also apply a transformation of
rotation, e.g. by 45ο…
Why not then take advantage
of this observation to construct
a simple mathematical model
that would describe this type
of complexity?

8. Could we build realistic models of trees and plants, if we
follow a self-similar construction of patterns at smaller and
smaller scales?
One answer is revealed by the theory
of Iterated Function Systems,
introduced by the American
Mathematician Michael Barnsley, in the
1980’s..
Barnsley proved that a sequence of
contracting transformations applied to
an original shape has always the same
limit no matter what the initial shape
is.
In other words, what matters is the
contracting transformations and not the
shapes we start with….

9. If we take an
initial shape and
contract it into 3
smaller ones
applying a rotation
to two of its
parts by 90ο (one
to the right the
other to the
left)…
…we obtain in
the end a shape
that looks like a
christmas tree
(see figure on
the left)…

10. …if together
with rotation
we also shift
the top piece
to the left,
we may design
ivy-looking
plants climbing
the walls of
our house…
What other
plants can we
design?

11. Let us use, for example, 4
such transformations, to
construct the leaf of a fern
plant, with infinitely many
smaller leaves on it:
Start with rectangle 1 for
the main leaf, 2 and 3 for
its two neighbors and 4 for
its very thin stem,….
Now observe what happens
after many iterations of this
process…

12. Isn’t it fascinating?
We can now start to
imitate Mother
Nature by drawing
pictures of real –
looking plants and
bushes, like
Barnsley’s fern
shown here……
All these objects are
called fractals and obey
a new kind of Geometry,
called Fractal Geometry!

13. Fractals and Chaos:
From Geometry to Dynamics!
Chaos is complexity in time, or, in other
words, the extremely sensitive dependence
of the motion on its initial conditions!
The first one who studied it was the French
Mathematician Henri Poincaré (1854 –
1912) shown here on the right.
In fact, Chaos can emerge out of a “fractal tree” of successive
bifurcations as a parameter r increases in a simple model of
population of rabbits living on an island!

14. As the growth
parameter r of
the rabbits
increases....
Xn
Here is where
chaos first
appears in the
population....
r

15. The concept of a bifurcation
is a lot more general in
nature. If you introduce
cockroaches in a dish with
two identical shelters, they
will first visit each shelter in
equal percentages, but
eventually, as the shelters’
capacity grows, they will all
end up visiting only one of the
shelters!
Note that this “collective
change of behavior” occurs,
without any apparent
communication between the
cockroaches!
J.-M. Amé, J. Halloy, C. Rivault, C. Detrain, and J.-L. Deneubourg, PNAS 103 (2006) 5835.

16. COLLECTIVE BEHAVIOR OF BIRDS, FISH,
TRAFFIC AND PEOPLE?
Out of chaos, patterns emerge
due to self - organization...

17. Work with C. Antonopoulos, V.
Basios and A. Garcia-Cantu Ros How can we model
(Chaos, Solitons & Fractals, 2011,
Vol. 44, 8, 574-586)
this phenomenon?
1. We first provide the
free particles with an inner
steering mechanism:
+/- ∆0

18. 2. Next, we include interactions with
nearby flock mates, so that two particles
interact (avoiding collisions)
3. Finally, we introduce a time-dependent coupling parameter φti from..
Periodic domain
Weakly chaotic
domain
Strongly
chaotic domain
0 φti 1

19. We find the following patterns of motion:
(a) Chaotic flight, (b) synchronized rotation or (c) “flocking”,
depending on whether φit belongs to:
(a) The strongly chaotic, (b) periodic or (c) weakly chaotic regimes.
with random initial conditions and FREE boundary conditions

20. 100 birds starting in the chaotic region, as time passes,
gather near the domain of weakly chaotic motion

21. Birds starting with parameters only in the chaotic region
tend towards the flocking (weak chaos) region!

22. Do pedestrians behave as individuals or social beings?
Observe how lanes of uniform walking direction
emerge due to self-organization.
Taken from: Dirk Helbing, Chair of
Sociology, in particular of Modeling
and Simulation, ETH Zürich
www.soms.ethz.ch

23. Helbing’s Intelligent Driver Model (IDM)
....produces the “waves of
congestion” or “clustering”
of cars we commonly
observe on the highways,
moving backward in time:
Martin Treiber, Ansgar Hennecke, and Dirk Helbing, “Congested Traffic States in Empirical Observations
and Microscopic Simulations”, Phys. Rev. E 62, 1805–1824 (2000)

24. Recent work of our group in Patras with Prof. Ko van der
Weele connects Granular Transport and…… Traffic Flow !
Q in
Q out
The dynamics of the grains involves a certain Flux
function F(nk), which must be specified in advance!

25. As a model we used the Eggers flux function:
2
 BR , L nk
FR, L (nk )  2
Ank e
...which follows the
reasonable argument that
for few particles in the k-
Here box the flux increases but
BR = 0.1
beyond a certain maximum
the flux will have to
decrease!
i.e., hL = 2hR
BL = 0.2
J. Eggers, PRL 83 (1999); KvdW, G. Kanellopoulos, Ch. Tsiavos, D. van der Meer, PRE 80 (2009)

26. Watch how the grain density along a 25-
step staircase becomes unstable as Q grows!
Q = 1.00 (relatively small)
Stable dynamic equilibrium: outflow = inflow

27. Increasing the inflow rate Q, a
“backward” wave develops...
outflow = inflow
Q = 1.80

28. … leading to a critical value: Qcrit = 1.8740
outflow
vanishes
….where clustering occurs at the top of the staircase!

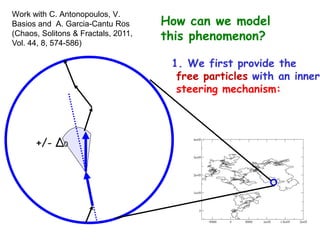
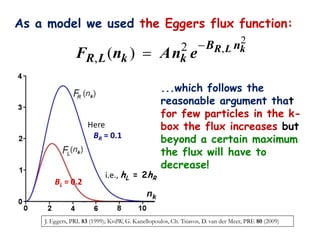
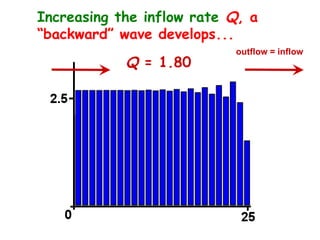
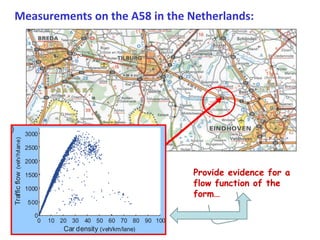
29. Traffic flow: Unidirectional version of the
staircase problem
[veh/ h per lane]
Δx = 500 m
with ρk(t) = car density in cell k [veh/km per lane]
A similar equation is obeyed here as with granular transport:
d k
x  F ( k 1 )  F ( k )  Qk (t )
dt
time step dt = 12 s (= Δx/vmax) in- and outflow
(only in certain cells k)
Now the Flux function F(ρk) is measured by induction loops at
periodic locations in the asphalt of the highway!

30. Measurements on the A58 in the Netherlands:
(b)
3000
Traffic flow (veh/h/lane)
2500
2000
1500 Provide evidence for a
flow function of the
1000
form…
500
0
0 10 20 30 40 50 60 70 80 90 100
Car density (veh/km/lane)

31. Observe the waves of congestion traveling backward! The front
lane is the slow on (90 km/hr) and the back the fast one (100 km)

32. Finally, about Biology: How can we model diseases
like ischemia or cardiac infarction of the heart?
Work of Dr. Adi Cimponeriu, T. Bezerianos, F. Starmer and T. Bountis at
the Department of Medicine of the University of Patras

33. We can model electrical pulse propagation through ion channels
by a one-dimensional array of electrical oscillators.....
....obeying the well-
known Kirchoff laws:

36. Normal (healthy) behavior

37. Non-normal (ischemic) propagation

38. The action potential “breaks” at the necrotic region and may develop spiral
waves that lead to arrythmia.....

39. In conclusion:
Complexity Science:
 Offers a unified methodology to study complex
physical, biological and social system.
 Familiarizes us with Mathematics, the common
language of all sciences, through the use of models.
 Proposes new concepts, principles and techniques to
better understand and perhaps predict and control
complex phenomena.
 Makes young people enjoy science, because it
excites their curiosity and imagination and make
them appreciate the interdisciplinary connections
between different scientific fields.

40. Of course, Hamlet may well advise us here:
«There are many more things on earth and
heaven, Horatio, than are dreamt in your
philosophy....»
Still, Complexity Science through the use
of mathematical modeling opened a new
“window” of communication with nature,
through which we have begun to glimpse the
“global picture” of ourselves and the world
that surrounds us…..

41. References
• G. Nicolis & I. Prigogine, “Exploring Complexity”
Freeman, New York (1989)
• T. Bountis, “The Wonderful World of Fractals” (in Greek),
Leader Books, Athens (2004).
• G. Nicolis and C. Nicolis, “Foundations of
Complex Systems”, World Scientific, Singapore, 2007
• C. Tsallis, “Introduction to Nonextensive Statistical
Mechanics: Approaching a Complex World”, Springer, New
York (2009).
• T. Bountis and H. Skokos, “Complex Hamiltonian
Dynamics”, Synergetic Series, Springer (April, 2012).