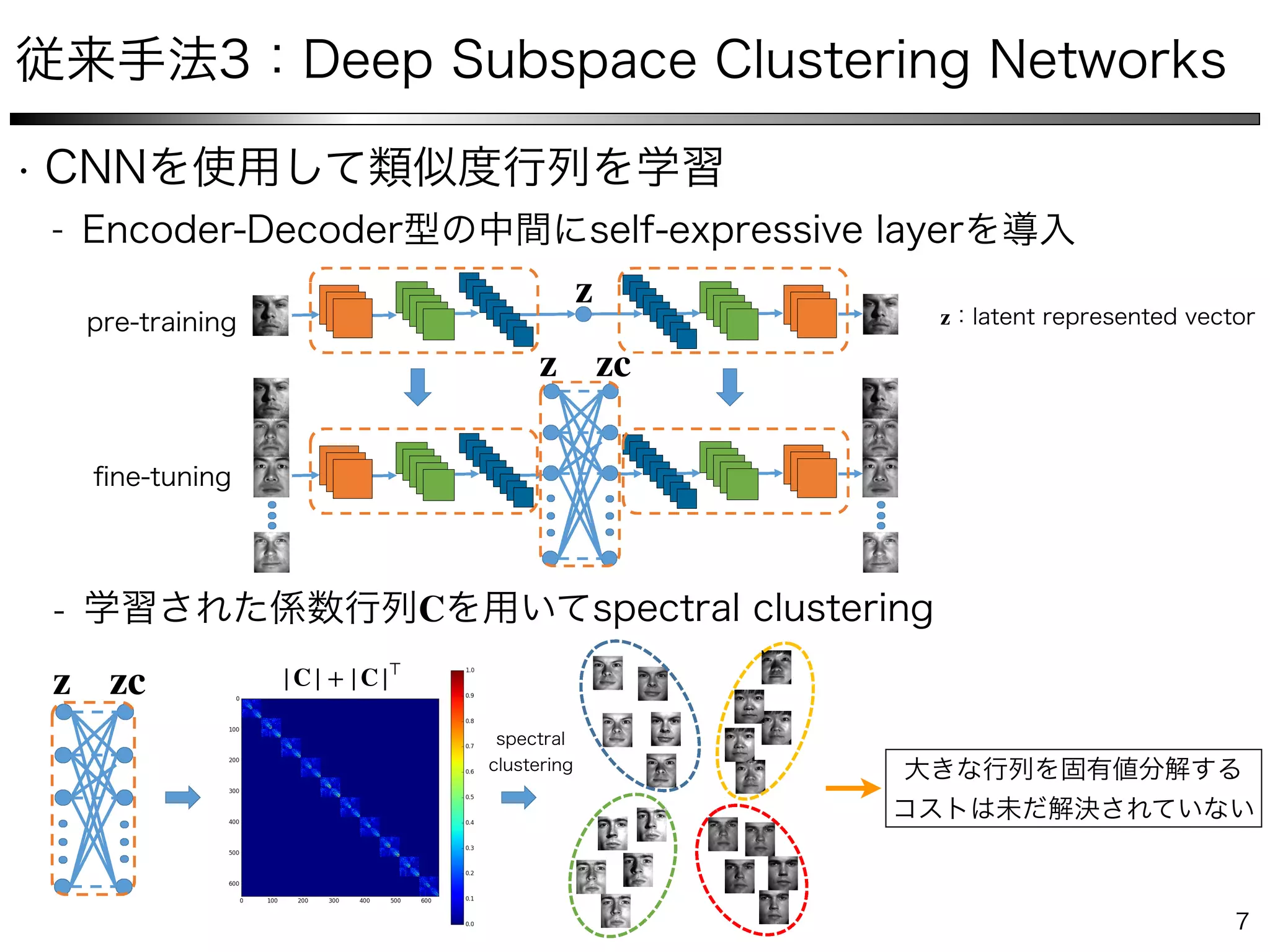
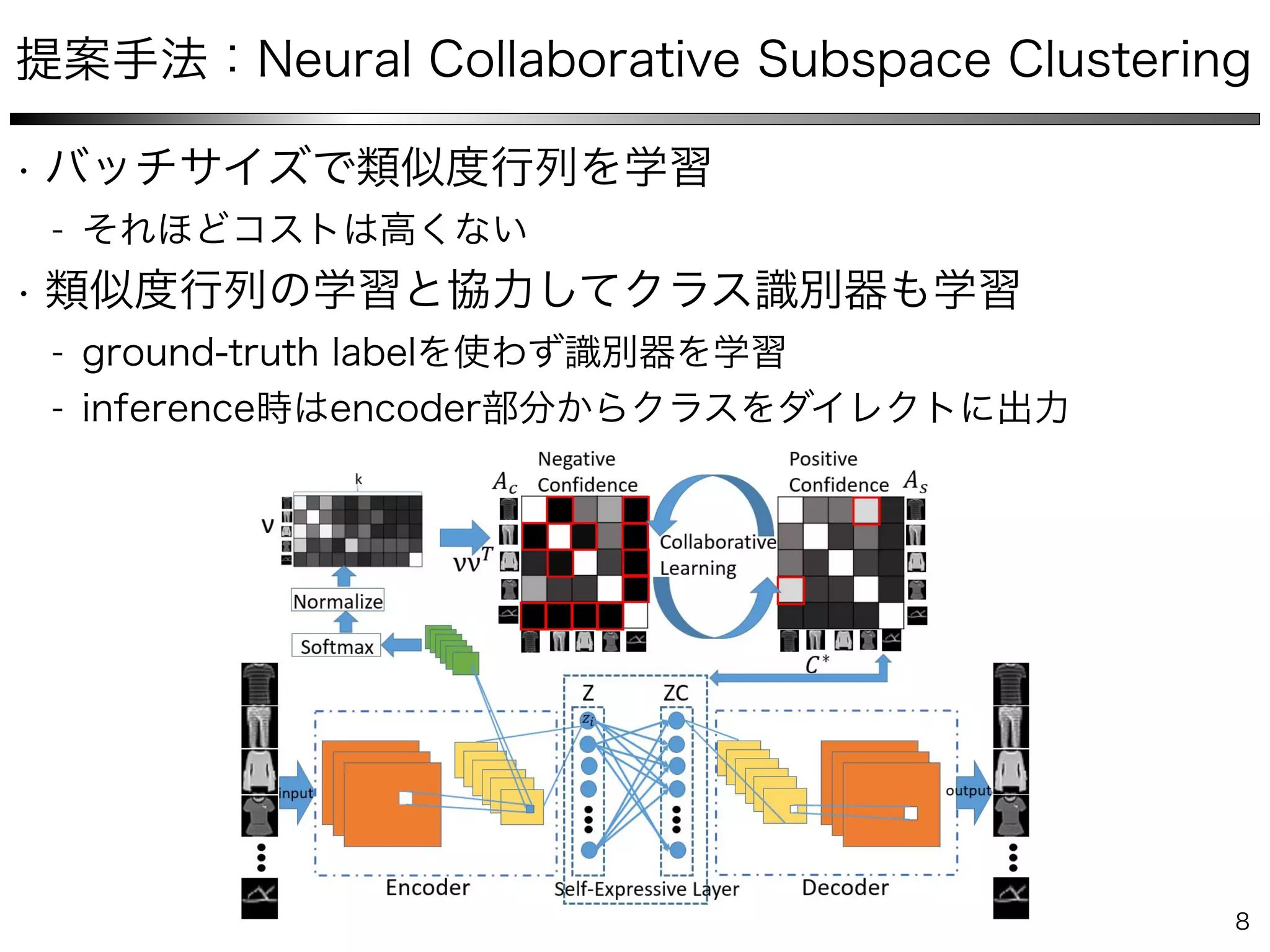
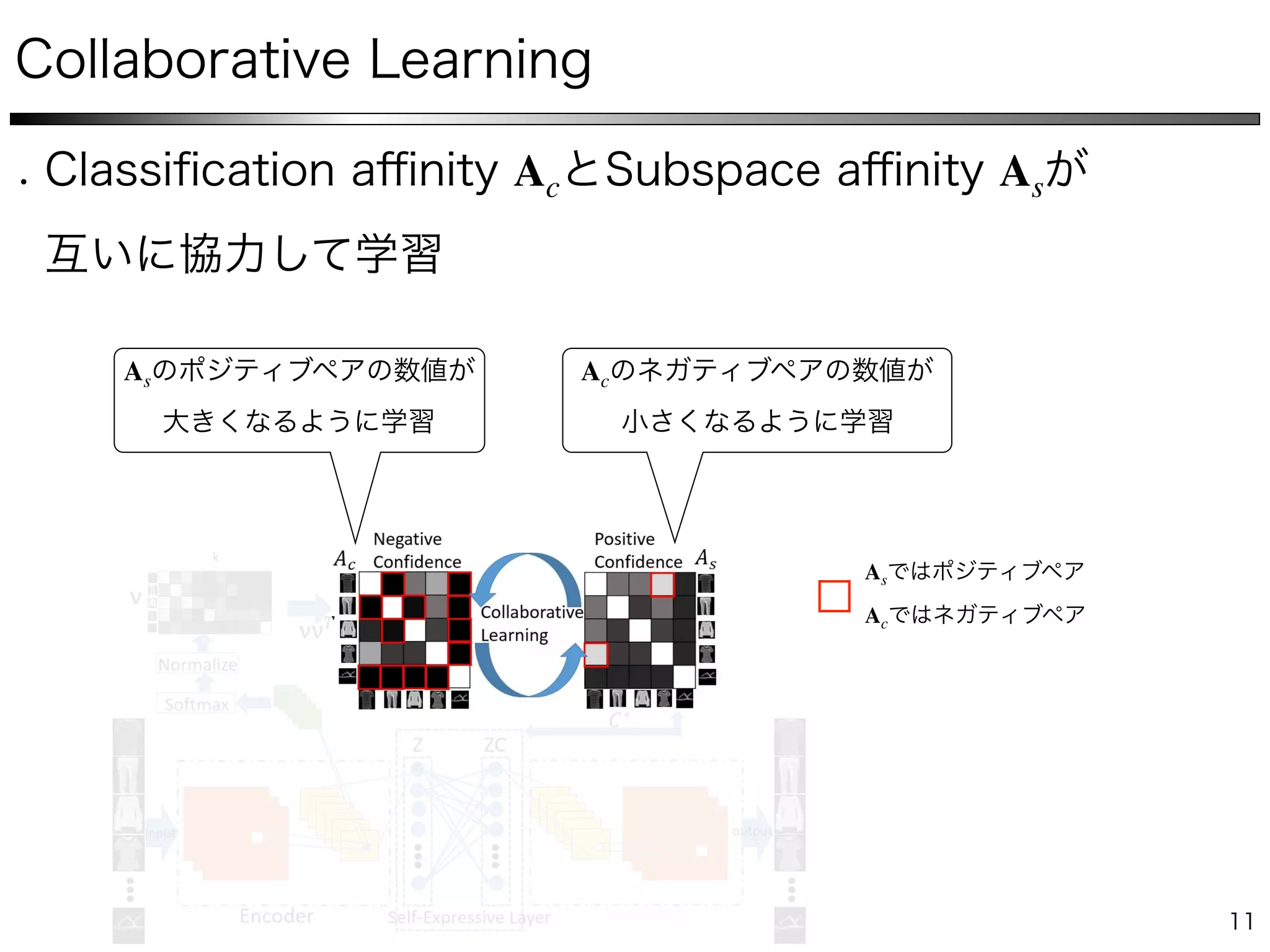
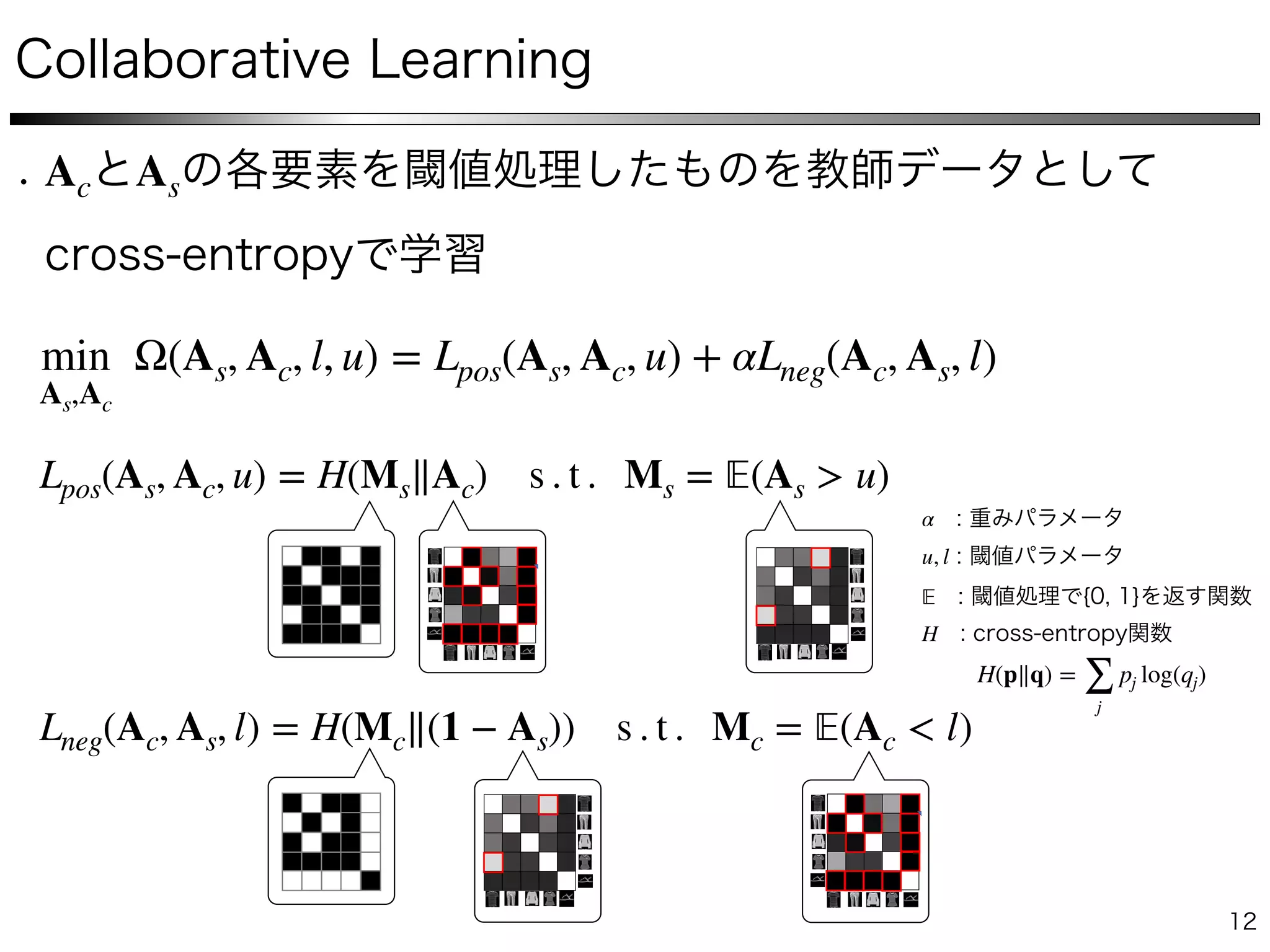
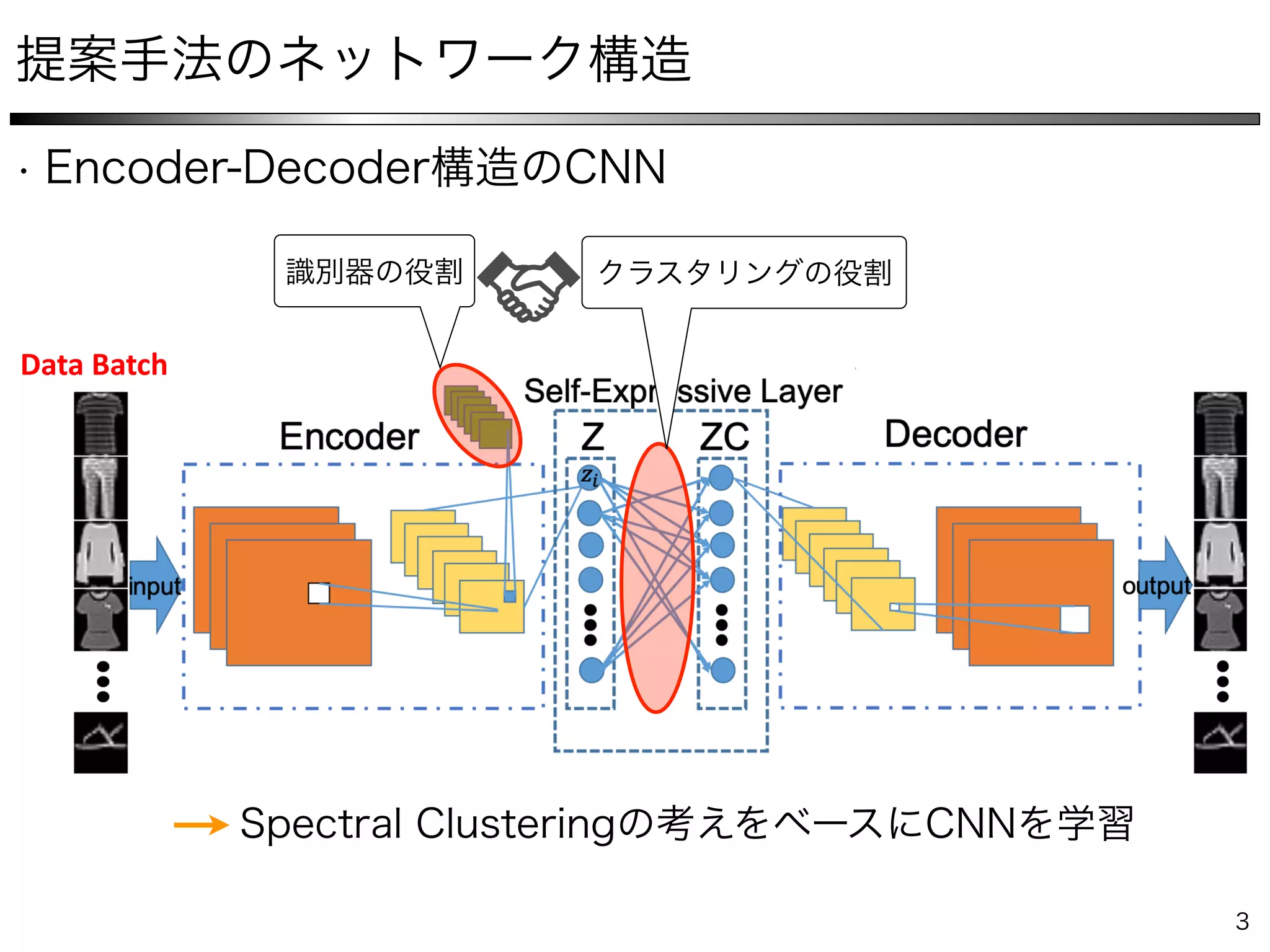
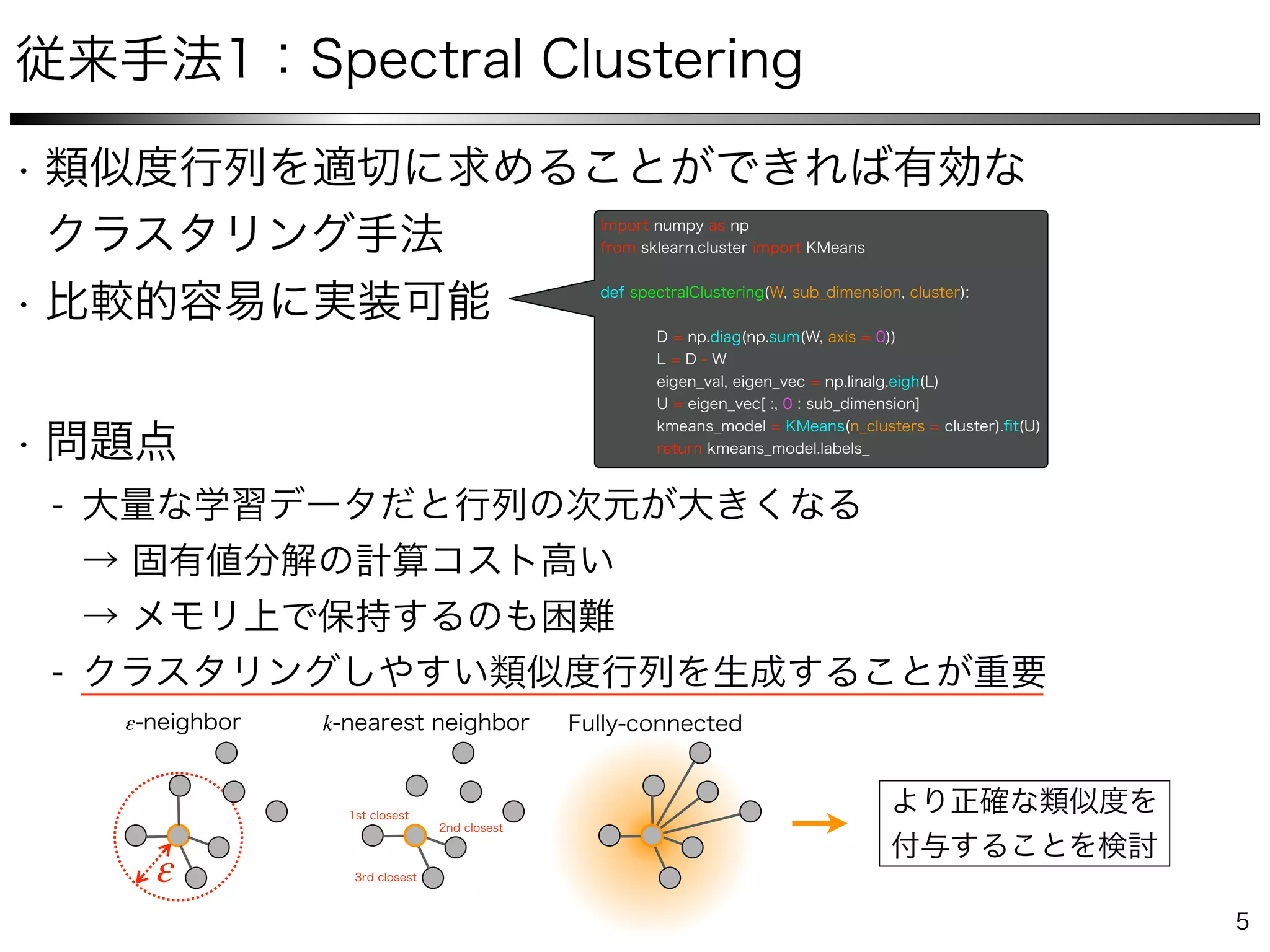
The document describes a method for collaborative subspace clustering using a deep neural network. The network contains an encoder, a self-expressive layer to learn the affinity matrix C, and a decoder. The network is trained end-to-end by minimizing a loss function containing terms for subspace clustering and collaborative learning between the affinity matrix C and a classifier's output affinity matrix. The loss encourages C to be more confident in identifying points from the same class compared to the classifier.


![min
C
∥C∥p s . t . X = XC, diag(C) = 0 X ∈ ℝD×N
X = [x1, x2, ⋯, xN]
xi D
C ∈ ℝN×N 4
S1
S2
S3
yi
0 5 10 15 20 25 30
−0.05
0
0.05
0.1
q = ∞
0 5 10 15 20 25 30
−0.1
−0.05
0
0.05
0.1
0.15
q = 2
0 5 10 15 20 25 30
−0.2
0
0.2
0.4
q = 1
Fig. 3. Three subspaces in R3
with 10 data points in each subspace, ordered such that the fist and the last 10 points belong to S1 and
S3, respectively. The solution of the `q-minimization program in (3) for yi lying in S1 for q = 1, 2, 1 is shown. Note that as the value of q
decreases, the sparsity of the solution increases. For q = 1, the solution corresponds to choosing two other points lying in S1.
Different choices of q have different effects in the obtained
solution. Typically, by decreasing the value of q from infinity
toward zero, the sparsity of the solution increases, as shown in
Figure 3. The extreme case of q = 0 corresponds to the general
NP-hard problem [51] of finding the sparsest representation of
the given point, as the `0-norm counts the number of nonzero
elements of the solution. Since we are interested in efficiently
whose nonzero elements correspond to points from the same
subspace of the given data point. This provides an immediate
choice of the similarity matrix as W = |C| + |C|>
. In other
words, each node i connects itself to a node j by an edge whose
weight is equal to |cij|+|cji|. The reason for the symmetrization
is that, in general, a data point yi 2 S` can write itself as a
linear combination of some points including yj 2 S`. However,
4
S1
S2
S3
yi
0 5 10 15 20 25 30
−0.05
0
0.05
0.1
q = ∞
0 5 10 15 20 25 30
−0.1
−0.05
0
0.05
0.1
0.15
q = 2
0 5 10 15 20 25 30
−0.2
0
0.2
0.4
q = 1
Fig. 3. Three subspaces in R3
with 10 data points in each subspace, ordered such that the fist and the last 10 points belong to S1 and
S3, respectively. The solution of the `q-minimization program in (3) for yi lying in S1 for q = 1, 2, 1 is shown. Note that as the value of q
decreases, the sparsity of the solution increases. For q = 1, the solution corresponds to choosing two other points lying in S1.
Different choices of q have different effects in the obtained
solution. Typically, by decreasing the value of q from infinity
toward zero, the sparsity of the solution increases, as shown in
Figure 3. The extreme case of q = 0 corresponds to the general
NP-hard problem [51] of finding the sparsest representation of
the given point, as the `0-norm counts the number of nonzero
elements of the solution. Since we are interested in efficiently
whose nonzero elements correspond to points from the same
subspace of the given data point. This provides an immediate
choice of the similarity matrix as W = |C| + |C|>
. In other
words, each node i connects itself to a node j by an edge whose
weight is equal to |cij|+|cji|. The reason for the symmetrization
is that, in general, a data point yi 2 S` can write itself as a
linear combination of some points including yj 2 S`. However,
4
S1
S2
S3
yi
0 5 10 15 20 25 30
−0.05
0
0.05
0.1
q = ∞
0 5 10 15 20 25 30
−0.1
−0.05
0
0.05
0.1
0.15
q = 2
0 5 10 15 20 25 30
−0.2
0
0.2
0.4
q = 1
Fig. 3. Three subspaces in R3
with 10 data points in each subspace, ordered such that the fist and the last 10 points belong to S1 and
S3, respectively. The solution of the `q-minimization program in (3) for yi lying in S1 for q = 1, 2, 1 is shown. Note that as the value of q
decreases, the sparsity of the solution increases. For q = 1, the solution corresponds to choosing two other points lying in S1.
Different choices of q have different effects in the obtained
solution. Typically, by decreasing the value of q from infinity
toward zero, the sparsity of the solution increases, as shown in
Figure 3. The extreme case of q = 0 corresponds to the general
NP-hard problem [51] of finding the sparsest representation of
the given point, as the `0-norm counts the number of nonzero
elements of the solution. Since we are interested in efficiently
whose nonzero elements correspond to points from the same
subspace of the given data point. This provides an immediate
choice of the similarity matrix as W = |C| + |C|>
. In other
words, each node i connects itself to a node j by an edge whose
weight is equal to |cij|+|cji|. The reason for the symmetrization
is that, in general, a data point yi 2 S` can write itself as a
linear combination of some points including yj 2 S`. However,
p = ∞ p = 1p = 2
{S1, S2, S3}
4
S1
S2
S3
yi
0 5 10 15 20 25 30
−0.05
0
0.05
0.1
q = ∞
0 5 10 15 20 25 30
−0.1
−0.05
0
0.05
0.1
0.15
q = 2
0 5 10 15 20 25 30
−0.2
0
0.2
0.4
q = 1
Fig. 3. Three subspaces in R3
with 10 data points in each subspace, ordered such that the fist and the last 10 points belong to S1 and
S3, respectively. The solution of the `q-minimization program in (3) for yi lying in S1 for q = 1, 2, 1 is shown. Note that as the value of q
decreases, the sparsity of the solution increases. For q = 1, the solution corresponds to choosing two other points lying in S1.
Different choices of q have different effects in the obtained
solution. Typically, by decreasing the value of q from infinity
toward zero, the sparsity of the solution increases, as shown in
Figure 3. The extreme case of q = 0 corresponds to the general
NP-hard problem [51] of finding the sparsest representation of
the given point, as the `0-norm counts the number of nonzero
whose nonzero elements correspond to points from the same
subspace of the given data point. This provides an immediate
choice of the similarity matrix as W = |C| + |C|>
. In other
words, each node i connects itself to a node j by an edge whose
weight is equal to |cij|+|cji|. The reason for the symmetrization
is that, in general, a data point yi 2 S` can write itself as a
xiS1
S2
S3
W = |C| + |C|⊤ ( wi,j = |ci,j | + |cj,i | ) W ∈ ℝN×N
C = C⊤](https://image.slidesharecdn.com/icml2019neuralcollaborativesubspaceclustering-190804015812/75/Neural-Collaborative-Subspace-Clustering-6-2048.jpg)